Kvant. Угол падения равен
Стасенко А.Л. Угол падения равен... //Квант. — 2005. — № 1. — С. 31,34.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
... Стоит лишь вынести нам под открытое звездное небо
Полный водою сосуд, как сейчас же в нем отразятся
Звезды небес и лучи засверкают на глади зеркальной.
Лукреций. О природе вещей
Ну кто же не знает, чему равен угол падения, конечно, углу отражения. А еще кое-что известно и о преломлении света. Вспомним построение лучей, которое предложил Христиан Гюйгенс — голландский физик, механик, математик и астроном.
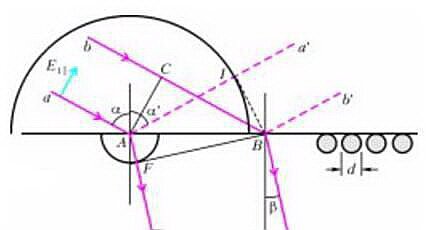
Пусть на плоскую границу двух сред, например воздух-вода, падают параллельные лучи света под углом α (рис.1) и луч а достигает границы в момент времени t = 0 в точке А. Участок фронта падающей волны (плоскость, перпендикулярная лучам) обозначим АС. Чтобы достигнуть поверхности раздела в точке В, луч b должен пройти путь СВ за время \(~t = \frac{CB}{\upsilon_1}\), где υ1 скорость света в первой среде...
И тут Гюйгенс ввел очень плодотворное понятие. Он предложил каждую точку поверхности раздела, до которой дошел падающий луч, т.е. первичная волна, считать источником сферической вторичной волны. Значит, пока луч b добирался до поверхности, точка А излучала вторичные волны — конечно, и в первую, и во вторую среду. Но скорости этой вторичной волны в двух средах различны — пусть, например, υ1 > υ2, как это имеет место в случае пары воздух-вода. А именно, за время t вторичная волна пройдет расстояние AI = υ1t в первой среде и AF = υ2t — во второй. Поэтому на рисунке 1 мы провели окружности разных диаметров, а через I и F обозначили точки касания фронтов отраженной и преломленной волн, которые (фронты) тожеперпендикулярны соответствующим лучам. Из равенства сторон треугольников АВС и ABI легко понять, что угол отражения α’ равен углу падения α. А для определения угла преломления β напишем (учитывая, что СВ = AI)
откуда следует известный закон преломления
Учитывая, что, по определению, коэффициент преломления среды обратно пропорционален скорости распространения света в этой среде, предыдущее соотношение можно записать в виде
где n — коэффициент преломления второй среды по отношению к первой.
Казалось бы, все ясно. Но вдумаемся в смысл приведенных выше слов. Прежде всего — что это за точка А, которая умеет излучать вторичные волны? В физике точек не существует. Есть электроны, ядра, атомы, молекулы... Все эти частицы имеют конечные размеры. Например, диаметр молекулы воды d составляет несколько ангстрем (1A = 10-10 м). Правда, средняя длина волны видимого нами света в тысячу раз больше: λ ~ 0,5 мкм = 5000 A. Поэтому в пределах одной молекулы электрическое и магнитное поля падающей (первичной) волны можно считать однородными, хотя, конечно, изменяющимися во времени с колоссальной частотой
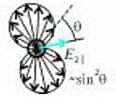
С этой частотой электрическое поле вынуждает колебаться электронные облака молекул относительно ядер. Таким образом, каждая молекула превращается в элементарную антенну, которая и обязана излучать (вторичную) волну той же частоты, что и падающая. Но, как известно, линейно колеблющийся диполь ничего не излучает вдоль линии своих колебаний, так же, как и прямолинейная антенна не излучает вдоль своей осевой линии. По секрету скажем даже больше: плотность потока электромагнитной энергии от диполя или линейной антенны (диаграмма направленности) пропорциональна sin2 θ, где θ — угол между направлением колебаний заряда (или тока) и линией наблюдения.
На рисунке 2 изображена отдельная молекула-диполь и качественно показана диаграмма направленности ее излучения. (Подробнее об этом можно прочитать, например, в недавней статье А. Стасенко «Небо синее, Солнце красное» в «Кванте» №1 за 2003 г. — Прим. ред.)
Теперь представим, что падающий свет линейно поляризован, а именно — его электрический вектор \(~\vec E_{1||}\) лежит в плоскости падения. Значит, в этой же плоскости будет лежать и вектор \(~\vec E_{2||}\) преломленной волны. И вот тут возникает интересный вопрос. Давайте подберем угол падения таким, чтобы направление отраженного луча было перпендикулярным преломленному лучу\[~\pi - \alpha' - \beta = \frac{\pi}{2}\] . Значит, при этом \(~\beta = \frac{\pi}{2} - \alpha' = \frac{\pi}{2} - \alpha\) . Подставив это значение угла преломления в закон преломления, получим
Этот особенный угол падения называется углом Брюстера.
Что же получается — если все молекулы второй среды, попавшие в область преломленного луча, колеблются в направлении α’ = α, то никакого излучения в направлении отраженного луча быть не может? Вот вам и «угол падения равен углу отражения»! Вся энергия ушла во вторую среду.
Но как же в таком случае мы в действительности наблюдаем отраженные лучи? Дело в том, что падающий свет не обязательно поляризован в плоскости падения. Обычно в нем присутствуют и колебания вектора \(~\vec E_{1 \perp}\) в перпендикулярной плоскости (так называемый хаотически, или естественно поляризованный свет). А эту составляющую молекулы второй среды переизлучают в направлении отраженного луча даже в случае угла Брюстера. Кроме того, отражающие поверхности не обязательно все расположены под углом Брюстера по отношению к падающему свету (в случае рассеянного света это невозможно даже для одной плоскости).
Угол Брюстера очень интересен для экспериментатора. Действительно, если поляризованный в плоскости падения луч направить на плоскость диэлектрика и измерить угол падения, при котором исчезнет отраженный луч, то можно по формуле tg α = n сразу определить коэффициент преломления среды. И сделать это можно, даже если диэлектрик непрозрачен и в нем невозможно наблюдать преломленный луч.
А как сделать этот падающий луч плоскополяризованным? Теперь ясно, как: нужно хаотически поляризованный луч предварительно отразить под углом Брюстера от пластинки из диэлектрика — при этом в отраженном луче останется только одно направление колебаний вектора \(~\vec E_{1 \perp}\).
Итак, кто же отражает и преломляет лучи света? Во всяком случае ясно, что не плоскость АВ (см. рис.1). И не один только поверхностный слой молекул. Для того чтобы «понять», что пора преломиться, падающий луч должен «ощупать» вещество на глубину, по крайней мере, сравнимую с его длиной волны, т.е. охватить тысячи слоев молекул. (Понятно, что имеется в виду длина волны во второй среде. Если последняя имеет коэффициент преломления n > 1, то \(~\lambda_2 = \frac{\lambda_1}{n} < \lambda_1\), но по порядку величины обе длины волны сравнимы.)
Теперь можно уточнить и определение «зеркальной» поверхности, упомянутой в эпиграфе Лукреция: ее шероховатости должны быть много меньше длины волны λ1 падающего излучения. (Отметим, что здесь идет речь о диэлектриках; в случае проводников, в которых имеются свободные электроны, процессы преломления и отражения имеют свои особенности.)
Наконец, что такое вообще параллельные падающие «лучи a и b»? Чтобы эти лучи были параллельны, должен падать достаточно широкий пучок света. Мы уже знаем, какой: его ширина должна быть много больше длины волны.
В результате всех рассуждений мы приходим к цепочке неравенств
На практике диаметр пучка в один миллиметр вполне удовлетворит этим неравенствам.
Однако, как далеко мы ушли от геометрической картинки рисунка 1: оказывается, не существует ни «плоскости» отражения, ни «лучей». Но не надо расстраиваться — геометрическая оптика все равно практически полезна, когда мы имеем дело с макроскопическими телами (окулярами, объективами, телескопами...), размеры которых много больше длины волны. А физическую оптику можно изучить, поступив в соответствующий институт или университет. Чего вам и желаем.