Kvant. Небо синее, Солнце красное

Стасенко А.Л. Небо синее, Солнце красное //Квант. — 2003. — № 1. — С. 37-38.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Ни пустоты, ни тьмы нам не дано:

Есть всюду свет, предвечный и великий...

И. Бунин

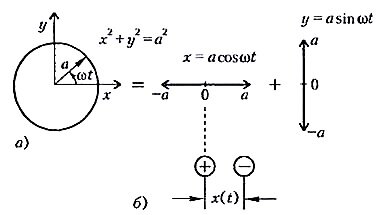
Как известно, антенны созданы для того, чтобы излучать и принимать электромагнитные волны. Отдельный атом тоже излучает, переходя в более низкое энергетическое состояние. Но он может и принимать электромагнитные волны определенных частот, возбуждаясь при этом, т.е. переходя в состояние с большей энергией. Так что атом в какой-то мере есть маленькая антенна. Только в атоме, согласно классической модели, электроны движутся по замкнутым траекториям, в простейшем случае - по окружностям. А движение по окружности (с радиусом a) можно представить как сумму двух гармонических колебаний, происходящих в той же плоскости, но во взаимно перпендикулярных направлениях и со сдвигом фаз 90° (рис. 1,а):

Рис. 1

\(~\begin{matrix} x = a \cos \omega t \\ y = a \sin \omega t \\ x^2 + y^2 = a^2 (\cos^2 \omega t + \sin^2 \omega t) = a^2\end{matrix}\) .

Рассмотрим поэтому движение зарядов только вдоль одной оси, например х.

Вообразим простейшую «антенну» в виде двух точечных одинаковых по модулю и противоположных по знаку зарядов ± q, расстояние между которыми в данный момент равно х(t) (рис. 1,б). Эта система зарядов - диполь - электрически нейтральна, тем не менее при постоянном значении х (плечо диполя) она создает электрическое дипольное поле, которое убывает с расстоянием быстрее, чем поле точечного заряда. Можно показать, что модуль напряженности дипольного поля пропорционален r^-3, но нас сейчас это статическое поле не интересует.

Пусть положительный заряд неподвижен (например, тяжелое ядро атома), а отрицательный («центр тяжести» электрона или электронного облака) движется относительно него. Чтобы точно описать возникающее переменное электромагнитное поле, необходимо использовать систему уравнений Максвелла, а в случае реального микрообъекта (атома) - и квантовую физику. Однако, этим лучше заняться, поступив в Московский физико-технический институт (или в Московский университет). Сейчас же постараемся сделать некоторые приближенные оценки, опираясь на теорию размерностей и сведения об электромагнетизме из школьной физики. Для удобства даже перенумеруем необходимые нам качественные соображения.

1. Неподвижный заряд не излучает энергию. То же очевидно и в отношении заряда, движущегося с постоянной скоростью (равномерно и прямолинейно). Иначе его излучение можно было бы использовать, скажем, для определения того, какая из инерциальных систем отсчета движется, а какая неподвижна, что запрещено в физике.

   Итак, излучать энергию может только заряд, движущийся ускоренно. Например, заряд, колеблющийся по упомянутому выше гармоническому закону \(~x(t) = a \cos \omega t\), заведомо движется ускоренно,и его ускорение равно \(~x'' = -\omega^2 x(t)\).

2. Энергия, излучаемая ускоренно движущимся зарядом, течет в радиальном направлении (не обязательно равномерно по всем направлениям; рис.2). При этом предполагается, что излучение рассматривается на больших расстояниях, намного превышающих амплитуду колебаний а.

   

   Рис. 2

   Кроме того, энергия течет от излучающего заряда, независимо от того, движется ли он вправо или влево от положения равновесия. Значит, поток энергии должен зависеть от четной степени ускорения. Какой именно? Ну конечно, второй, поскольку...

3. Плотность потока энергии электромагнитной волны пропорциональна произведению электрического и магнитного полей, а последние пропорциональны друг другу, в силу линейности уравнений электромагнетизма.

   Уже то, что мощность излучения пропорциональна четвертой степени частоты (W ~ х’’² ~ ω⁴), позволяет объяснить такой красивый факт природы, как голубизна неба. Дело в том, что Солнце излучает довольно широкий спектр длин электромагнитных волн λ (рис.3). Наш глаз приспособился видеть основную, наиболее энергетичную часть, заключенную в пределах λ = 0,4 - 0,8 мкм. Короткие волны соответствуют фиолетовому концу этого спектра, длинные - красному. Но чем меньше длина волны, тем выше частота (\(~\omega = \frac{2 \pi c}{\lambda}\)) . И, согласно полученному выше соотношению, короткие (или высокочастотные) волны, возбуждая частицы атмосферы (и таким образом превращая их в излучающие диполи), должны рассеиваться сильнее длинных - да еще в четвертой степени (см. точечную кривую на рисунке 3).

   

   Рис. 3

   Ясно также, почему Солнце кажется красным на закате: в это время его лучи проходят в атмосфере самый длинный путь, и из них отсеиваются во все стороны именно голубые лучи, что относительно обогащает красную часть спектра.

   Но продолжим рассуждения о структуре волны, излучаемой ускоренно движущимся зарядом.

4. Векторные линии магнитного поля \(~\vec B\) имеют вид окружностей в плоскостях, перпендикулярных направлению движения заряда, а поскольку векторы \(~\vec B\), \(~\vec c\) и \(~\vec E\) образуют правую тройку (электромагнитная волна поперечна), то вектор \(~\vec E\) должен быть направлен по касательной к сфере радиусом r. Все это и показано на рисунке 2.

Все, что мы наговорили до сих пор, дает возможность заключить, что излучаемая мощность может быть записана в виде W ~ q²х’’². А там, где появляется кулон в квадрате, в СИ всегда появляется множитель \(~\frac{1}{4 \pi \varepsilon_0}\), имеющий размерность м/Ф. Но ведь Кл²/Ф = Дж (вспомним хотя бы формулу для энергии конденсатора), а размерность W должна быть Вт = Дж/с. Следовательно, нужно еще разделить на куб скорости... чего? конечно же, света. Итак,

\(~W \sim \frac{q^2 x''^2}{4 \pi \varepsilon_0 c^3}\) .

Точная формула

\(~W = -\frac 23 \frac{q^2 x''^2}{4 \pi \varepsilon_0 c^3}\) , (*)

не намного отличается от полученного нами выражения (знак минус указывает на убыль энергии).

Но что же это получается? Электроны в атомах движутся вокруг ядер ускоренно (вспомним, что движение по окружности - ускоренное), значит, согласно изложенным представлениям классической физики, они должны излучать энергию и в конце концов упасть на ядра? Оценим время такого падения. Сумма кинетической и потенциальной энергий электрона на круговой орбите радиусом a равна

\(~E = \frac{m_e \upsilon^2}{2} - \frac{e^2}{4 \pi \varepsilon_0 a}\)

(здесь предполагается простейший случай атома водорода: m_e - масса электрона, е — его заряд). Учитывая, что сила Кулона сообщает электрону центростремительное ускорение:

\(~\frac{e^2}{4 \pi \varepsilon_0 a^2} = \frac{m_e \upsilon^2}{a}\) ,

найдем

\(~E = - \frac 12 \frac{e^2}{4 \pi \varepsilon_0 a}\) .

Разделив зту начальную (до излучения) суммарную энергию E на скорость ее потерь W, получим оценку времени излучения τ. Будем считать, что излучение происходит за много периодов колебаний, и осредним выражение (*) по времени. Используем известный факт\[~<\cos^2 \omega t> = \frac 12\]. Тогда

\(~\tau \sim \frac EW \sim \frac{1}{\omega^4} \left( \frac ca \right)^3 = \left( \frac{\lambda}{2 \pi} \right)^4 \frac{1}{a^3c}\) .

Подставим сюда характерные величины: длину волны, соответствующую максимуму солнечного спектра λ_m = 0,55 мкм (кстати, это зеленый свет, так что не случайно Солнце относится к спектральному классу зеленых звезд), и радиус орбиты a порядка 1 А (эта величина и введена специально для измерения атомарных размеров). В результате получим

\(~\tau \sim \frac{(5,5 \cdot 10^{-7})^4}{(2\pi)^4 \cdot (10^{-10})^3 \cdot 3 \cdot 10^8}\) ≈ 0,2·10^-6 с.

Значит, за доли микросекунды электроны должны были бы упасть на ядра, и наш мир перестал бы существовать!?

Но тут на помощью пришла квантовая теория: она разрешила электронам долго «жить» на избранных орбитах (подобно тому, как заботливое жилищное управление разрешает квартиросъемщикам спать на этажах, а не на лестничных маршах). Однако, это уже другая история...