Kvant. Колебания заряда

Стасенко А.Л. Колебания заряда и космическая оранжерея //Квант. — 1994. — № 5. — С. 43-45.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Запишем выражение для напряженности электрического поля Е на расстоянии r от точечного заряда Q (которое прямо следует из закона Кулона) в таком виде:

\(~E \cdot 4 \pi r^2 = \frac{Q}{\varepsilon_0}\) .

Рис. 1

Узнали? Только теперь его можно прочесть так: произведение напряженности электрического поля на площадь замкнутой поверхности, все элементы которой перпендикулярны вектору поля, пропорционально заряду, создавшему это поле (рис. 1). Это утверждение представляет собой частный случай основной теоремы электростатики — теоремы Гаусса. (В общем случае теорема Гаусса гласит: поток вектора напряженности электрического поля через замкнутую поверхность пропорционален величине заряда, находящегося внутри этой поверхности.)

Рис. 2

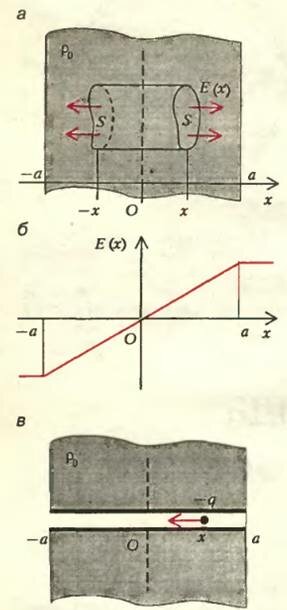
А теперь представим себе, что точечный заряд не один, их много, и все они «размазаны» внутри бесконечного слоя толщиной 2а (-а < х < а; рис.2) с постоянной объемной плотностью ρ₀. Интуитивно ясно, что электрическое поле в средней плоскости (x = 0) должно равняться нулю, так как силы, действующие влево и вправо на любой пробный заряд со стороны всех зарядов этого слоя, уравновешиваются.

Физик сказал бы, что это ясно из соображений симметрии. Из тех же соображений ясно, что если мы отступим от средней плоскости на расстояние |х| (все равно — внутри слоя или вне его) влево или вправо, то в плоскостях ±х электрические поля должны быть одинаковыми по модулю, но противоположными по направлению: Е(х) = -Е(-х), т.е. антисимметричными.

Применим теорему Гаусса к замкнутой поверхности — цилиндрику длиной 2х, образующая которого параллельна оси X, а два донышка имеют одинаковую площадь S (рис. 2, а). Тогда произведение напряженности поля на перпендикулярные ему площади\[~E(x) \cdot S + (-E(-x) \cdot S)\] должно быть пропорционально полному заряду внутри цилиндрика\[~Q = \rho_0 \cdot 2x \cdot S\]. Учитывая антисимметричность полей Е(х) и Е(-х), запишем

\(~2 E(x) \cdot S = \frac{\rho_0 \cdot 2x \cdot S}{\varepsilon_0}\) ,

откуда получаем

\(~E(x) = \frac{\rho_0}{\varepsilon_0} x\) ,

Эта зависимость поля от координаты изображена на рисунке 2, б в виде прямой линии (внутри слоя).

Ну и что тут интересного ? Статика она и есть статика. Но давайте теперь внутрь этого слоя поместим маленький отрицательно заряженный (-q) шарик. А чтобы он там не мешал распределенным зарядам, создающим поле, заключим его, например, в тонкую стеклянную трубочку, параллельную оси Х (рис. 2, в). Если он находится сейчас на расстоянии х от средней плоскости, то на него действует сила \(~F = -qE(x)\). Запишем второй закон Ньютона для шарика (пусть его масса m):

\(~x'' = -\frac qm E(x) = -\frac{q \rho_0}{m \varepsilon_0} x\) .

Сразу видно, что это уравнение гармонического колебательного движения с круговой частотой \(~\omega_0 = \sqrt{\frac{q \rho_0}{m \varepsilon_0}}\) . И этот шарик моделирует все гармонические колебания — ну например, какого-нибудь другого шарика, подвешенного на нити длиной l в поле тяготения и совершающего малые колебания с частотой \(~\omega_g = \sqrt{\frac gl}\).

А что если заряд внутри слоя распределен неравномерно? Допустим, его объемная плотность линейно изменяется по координате:

\(~\rho(x) = \rho_0 \frac{|x|}{a}\) .

Рис. 3

Это означает, что плотность нулевая в центре, а на границах слоя х = ±а она равна ρ₀ (рис. 3, а). Тогда полный заряд внутри нашего цилиндрика уже нельзя найти просто умножением плотности заряда на объем, а надо интегрировать по объему:

\(~Q(x) = 2 \int^x_0 \rho(x) S dx = 2 \rho_0 \frac{Sx^2}{2 a} = \frac{\rho_0 Sx^2}{a}\) .

Теорема Гаусса даст для поля выражение

\(~E(x) = \frac{\rho_0}{2 \varepsilon_0 a} x |x|\) ,

а уравнение движения шарика в трубочке примет вид

\(~x'' = -\frac qm E(x) = -\frac{q \rho_0}{2 m a \varepsilon_0} x|x| = -\beta^2_0 x|x|\) , (*)

где \(~\beta_0 = \frac{\omega_0}{\sqrt{2 a}}\) — новая положительная постоянная, а вместо х² написано более хитрое выражение x|x|, которое отражает тот факт, что напряженность поля направлена к средней плоскости х = 0 (рис. 3, б).

Это тоже уравнение колебаний. Но уже ни один здравомыслящий человек не назовет их гармоническими, ибо возвращающая сила пропорциональна не смещению, а его квадрату. Интересно, что период таких ангармонических колебаний зависит от амплитуды колебаний (см., например, статью А.Черноуцана «Гармонические колебания — обычные и удивительные» в «Кванте» № 9 за 1991 год.).

Можно было бы порезвиться и дальше: если взять ρ(х) ~ х² ,то электрическое поле будет пропорционально х³; если взять ρ(х) ~ х³, то Е ~ х⁴; если ρ(х) ~ х⁴, то... Но давайте посмотрим, нельзя ли использовать уже полученное уравнение ( * ) для какой-нибудь надобности — смоделировать что-нибудь более сложное, чем шарик в трубочке.

Рис. 4

Ну например, вообразим себе космическую оранжерею — цилиндр радиусом R, длиной L (L >> R) и массой М, которая вся распределена по поверхности цилиндра (внутри он пустой). Половина поверхности этого цилиндра пусть абсолютно прозрачна для солнечного излучения, которое падает слева и интенсивность которого равна Р (рис. 4). Другая же половина пусть полиостью поглощает излучение. Если в данной момент цилиндр повернут на угол θ , то излучение, поглощаемое участком АВ, не создает вращения вокруг оси цилиндра. А вот фотоны, поглощаемые участком CD, попытаются вращать оранжерею по часовой стрелке (так как участок ЛЯ прозрачен и не задерживает фотонов). Но по инерции положение равновесия θ = 0 будет пройдено, навстречу солнечным лучам выдвинется нижний поглощающий участок, так что возникнут вращательные колебания. Итак, если отклонить оранжерею от положения равновесия θ = 0 на какой-то начальный угол θ₀, она будет колебаться в солнечных лучах с угловой амплитудой θ₀ (если нет потерь энергии). И это покачивание вокруг оси для растений даже очень комфортно; центробежная сила инерции создает у них иллюзию поля тяготения (правда, переменного), и они в своем росте будут тянуться к оси вращения.

Составим уравнение колебательного движения оранжереи. Прежде всего найдем силу, действующую на поглощающий излучение участок CD перпендикулярно оси. Предполагая угол θ малым, получим, что длина отрезка CD приблизительно равна длине s дуги CD:

\(~CD = \breve{CD} = s = R \theta\) .

Мощность, поглощаемая этим участком, равна мощности излучения, прошедшего через перпендикулярную площадку CI:

\(~W = P \cdot CD \sin \left( \frac{\theta}{2}\right) \cdot L = \frac 12 PRL \theta^2\) .

А поскольку импульс каждого фотона получается делением его энергии на скорость света с, то поток импульса всех фотонов, поглощенных участком CD, т.е. сила, равен \(~\frac Wc\) . Тогда уравнение «движения массы М по окружности» примет вид

\(~Ms'' = MR \theta'' = -\frac{PRL}{2c} \theta|\theta|\) .

Здесь учтено, что вследствие малости угла θ сила действует почти по касательной к дуге окружности CD, а знак минус отражает тот факт, что сила направлена в сторону уменьшения угла θ (положительное значение которого отсчитывается против часовой стрелки) . Заметим, что то же самое уравнение получится и в случае цилиндра, одна половина которого зеркальная, а другая — черная.

Если теперь обе части равенства поделить на MR и обозначить

\(~\beta^2_0 = -\frac{PL}{2cM}\) ,

то получим уравнение, в точности совпадающее с ( * ). Хотя, казалось бы, что у них общего? Там — заряженный шарик в трубочке, а тут — оранжерея в солнечных лучах!

«...обогащение и рост интеллекта заключается в его способности нахо; лить подобия... все должно быть подобно друг другу, самая мельчайшая часть подобна целому, пылинка — вселенной, и все подобно Божеству. Что вверху, то и внизу» (П.Д.Успенский, Новая модель Вселенной).