Т. Центр инерции

Система материальных точек. Уравнение поступательного движения системы материальных точек. Центр инерции

Совокупность тел, рассматриваемых как единое целое, называют механической системой.

Силы, с которыми взаимодействуют материальные точки системы между собой, называют внутренними силами. Силы, с которыми на материальные точки системы действуют тела, не входящие в данную систему (внешние тела), называют внешними силами.

Механическая система тел, на которую не действуют внешние силы, называется замкнутой, или изолированной, системой.

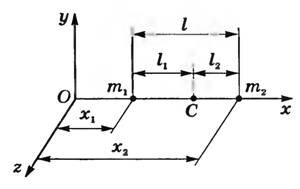
Для простоты рассуждений рассмотрим вначале систему, состоящую из двух материальных точек с массами m₁ и m₂, которые расположены на оси абсцисс в точках с координатами x₁ и x₂ (рис. 1). Расстояние между этими точками l = x₂ - x₁. Точку С, которая де лит это расстояние на отрезки, обратно пропорциональные массам, называют центром масс.

Рис. 1

Следовательно, по определению

\(~\frac{l_1}{l_2} = \frac{m_2}{m_1}. \qquad (1)\)

Пусть координата этой точки x_c тогда l₁ = x_c - x₁; l₂ = x₂ - x_c. Подставим в уравнение (1), получим\[~m_1 (x_c - x_1) = m_2 (x_2 - x_c)\]. Отсюда

\(~x_c = \frac{m_1x_1 + m_2x_2}{m_1 + m_2}. \qquad (2)\)

Формула (2) позволяет определить координату центра масс системы, состоящей из двух материальных точек.

Выражение (2) можно обобщить на систему n материальных точек, расположенных произвольным образом. Координата центра масс

\(~x_c = \frac{m_1x_1 + m_2x_2 + \ldots + m_nx_n}{m_1 + m_2 + \ldots + m_n}. \qquad (3)\)

Аналогичные выражения получаются и для координат y_c и z_c.

Положение центра масс можно также определить с помощью радиуса-вектора:

\(~\vec r_c = \frac{\sum^n_{i=1} m_i \vec r_i}{m_1 + m_2 + \ldots + m_n},\)

где m_i и \(~\vec r_i\) — масса и радиус-вектор i-й частицы.

При движении материальных точек системы координаты их изменяются. Записав выражение (3) для двух моментов времени t₁ и t₂, вычтем одно из другого и получим:

\(~\Delta x_c = \frac{m_1 \Delta x_1 + m_2 \Delta x_2 + \ldots + m_n \Delta x_n}{m_1 + m_2 + \ldots + m_n}.\)

Разделив обе части этого выражения на промежуток времени Δt = t₂ - t₁, имеем:

\(~\upsilon_{cx} = \frac{m_1 \upsilon_{1x} + m_2 \upsilon_{2x} + \ldots + m_n \upsilon_{nx}}{m_1 + m_2 + \ldots + m_n},\)

где υ_cx, υ_1x ... υ_nx — проекции на ось Ox векторов скорости движения центра масс и материальных точек 1, 2 ... n.

Аналогичные выражения можно записать и для проекции скорости на оси Оу и Oz.

Выражение для нахождения скорости движения центра масс в векторном виде:

\(~\vec \upsilon_c = \frac{m_1 \vec \upsilon_1 + m_2 \vec \upsilon_2 + \ldots + m_n \vec \upsilon_n}{m_1 + m_2 + \ldots + m_n}. \qquad (4)\)

При движении материальных точек системы центр масс перемещается. Определим, от чего зависит характер движения центра масс.

Для этого рассмотрим систему двух материальных точек. Пусть на эти материальные точки действуют внешние силы \(~\vec F_1\) и \(~\vec F_2\) и эти точки взаимодействуют между собой силами \(~\vec F_{12}\) и \(~\vec F_{21}\) (рис. 2).

Рис. 2

Запишем для каждой материальной точки второй закон Ньютона:

\(~\begin{matrix} m_1 \vec a_1 = \vec F_{12} + \vec F_1; \\ m_1 \vec a_2 = \vec F_{21} + \vec F_2. \end{matrix}\)

Выразим ускорение точек через их начальные \(~\vec \upsilon_1\) и \(~\vec \upsilon_2\) и конечные \(~\vec \upsilon_1\,'\) и \(~\vec \upsilon_2\,'\) скорости:

\(~\begin{matrix} \vec a_1 = \frac{\vec \upsilon_1\,' - \vec \upsilon_1}{\Delta t}; \\ \vec a_2 = \frac{\vec \upsilon_2\,' - \vec \upsilon_2}{\Delta t}. \end{matrix}\)

Подставим полученные выражения во второй закон Ньютона:

\(~\begin{matrix} m_1 (\vec \upsilon_1\,' - \vec \upsilon_1) = (\vec F_{12} + \vec F_1) \Delta t; \\ m_2 (\vec \upsilon_2\,' - \vec \upsilon_2) = (\vec F_{21} + \vec F_2) \Delta t. \end{matrix}\)

Складывая эти равенства, имеем:

\(~(m_1 \vec \upsilon_1\,' + m_2 \vec \upsilon_2\,') - (m_1 \vec \upsilon_1 + m_2 \vec \upsilon_2) = (\vec F_{12} + \vec F_{21}) \Delta t + (\vec F_1 + \vec F_2) \Delta t. \qquad (5)\)

Поскольку по третьему закону Ньютона \(~\vec F_{12} = -\vec F_{21}\), то \(~\vec F_{12} + \vec F_{21} = 0\). Из формулы (4) получаем:

\(~\begin{matrix} m_1 \vec \upsilon_1 + m_2 \vec \upsilon_2 = \vec \upsilon_c (m_1 + m_2); \\ m_1 \vec \upsilon_1\,' + m_2 \vec \upsilon_2\,' = \vec \upsilon_c\,' (m_1 + m_2). \end{matrix}\)

где \(~\vec \upsilon_c\) и \(~\vec \upsilon_c\,'\) — скорости движения центра масс в начальный момент времени и через промежуток времени Δt. Тогда равенство (5) можно записать так:

\(~(m_1 + m_2) \cdot (\vec \upsilon_c\,' - \vec \upsilon_c) = (\vec F_1 + \vec F_2) \Delta t. \qquad (6)\)

Выражение (6) показывает, что изменить скорость движения центра масс системы материальных точек могут только внешние силы, внутренние силы изменяют скорости движения отдельных материальных точек.

Обозначим m₁ + m₂ = M, где Μ — суммарная масса материальных точек системы. Следовательно,

\(~\frac{M(\vec \upsilon_c\,' - \vec \upsilon_c)}{\Delta t} = \vec F_1 + \vec F_2 \Rightarrow M \frac{\Delta \vec \upsilon_c}{\Delta t} = \vec F_1 + \vec F_2 \Rightarrow M \vec a_c = \vec F_1 + \vec F_2 \Rightarrow M \vec a_c = \sum^n_{i=1} \vec F_i. \qquad (7)\)

т. е. центр масс системы движется как материальная точка в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Выражение (7) представляет собой закон движения центра масс.

Если система материальных точек замкнутая, т. е. \(~\sum^n_{i=1} \vec F_i = 0\), то \(~M \vec a_c = 0\).

Следовательно, центр масс замкнутой системы материальных точек движется равномерно и прямолинейно либо остается неподвижным независимо от того, как движутся отдельные материальные точки системы.

Так, если в инерциальной системе отсчета центр масс замкнутой системы был неподвижен в какой-то момент времени, то он будет оставаться в покое, несмотря на движение отдельных материальных точек системы в результате их взаимодействия.

Таким образом, центр масс (центр инерции) системы, положение которого характеризует распределение масс этой системы и определяется формулой (3), а скорость которого определяется формулой (4), является характерной точкой для системы, поведение которой подчиняется законам Ньютона и не зависит от природы сил взаимодействия в системе.

Понятие центра масс относится и к одиночному телу, которое можно представить как совокупность материальных точек. Центр масс тела можно рассматривать как точку (находящуюся внутри тела или вне его), в которой пересекаются линии действия сил, приводящих данное тело в поступательное движение. Центр масс тела совпадает с его центром тяжести.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 43-46.