T. Магнитные св. вещества
Магнитные свойства вещества. Магнитная проницаемость
Многочисленные опыты свидетельствуют о том, что все вещества, помещенные в магнитное поле, намагничиваются и создают собственное магнитное поле, действие которого складывается с действием внешнего магнитного поля:
где \(~\vec B\) — магнитная индукция поля в веществе; \(~\vec B_0\) — магнитная индукция поля в вакууме, \(~\vec B_1\) — магнитная индукция поля, возникшего благодаря намагничиванию вещества. При этом вещество может либо усиливать, либо ослаблять магнитное поле. Влияние вещества на внешнее магнитное поле характеризуется величиной μ, которая называется магнитной проницаемостью вещества
Магнитная проницаемость — это физическая скалярная величина, показывающая, во сколько раз индукция магнитного поля в данном веществе отличается от индукции магнитного поля в вакууме.
Вещества, ослабляющие внешнее магнитное поле, называют диамагнетиками (висмут, азот, гелий, углекислота, вода, серебро, золото, цинк, кадмий и др.).
Вещества, усиливающие внешнее магнитное поле, — парамагнетики (алюминий, кислород, платина, медь, кальций, хром, марганец, соли кобальта и др.).
Для диамагнетиков μ<1, для парамагнетиков μ>1. Но в том и другом случае отличие μ от 1 невелико (несколько десятитысячных или стотысячных долей единицы). Так, например, у висмута μ = 0,9998 = 1,000.
Некоторые вещества (железо, кобальт, никель, гадолиний и различные сплавы) вызывают очень большое усиление внешнего поля. Их называют ферромагнетиками. Для них μ ≈ 103 -105 .
Впервые объяснение причин, вследствие которых тела обладают магнитными свойствами, дал Ампер. Согласно его гипотезе, внутри молекул и атомов циркулируют элементарные электрические токи, которые и определяют магнитные свойства любого вещества.
В настоящее время установлено, что все атомы и элементарные частицы действительно обладают магнитными свойствами. Магнитные свойства атомов в основном определяются входящими в их состав электронами.
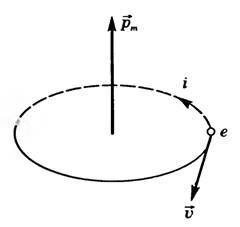
Согласно полуклассической модели атома, предложенной Э. Резерфордом и Н. Бором, электроны в атомах движутся вокруг ядра по замкнутым орбитам (в первом приближении можно считать, что по круговым). Движение электрона можно представить как элементарный круговой ток \(~i = e \cdot v\), где е — заряд электрона, ν — частота вращения электрона по орбите. Этот ток образует магнитное поле, которое характеризуется магнитным моментом, модуль его определяется формулой \(~p_m=iS = evS\), где S — площадь орбиты.
Магнитный момент электрона, обусловленный движением вокруг ядра, называют орбитальным магнитным моментом. Орбитальный магнитный момент — это векторная величина, и направление \(~\vec p_m\) определяется по правилу правого винта. Если электрон движется по ходу часовой стрелки (рис. 1), то токи направлены против хода часовой стрелки (по направлению движения положительного заряда), и вектор \(~\vec p_m\) перпендикулярен плоскости орбиты.
Так как в атоме плоскости орбит различных электронов не совпадают, то их магнитные моменты направлены под разными углами друг к другу. Результирующий орбитальный магнитный момент многоэлектронного атома равен векторной сумме орбитальных магнитных моментов отдельных электронов.
Нескомпенсированным орбитальным магнитным моментом обладают атомы с частично заполненными электронными оболочками. В атомах с заполненными электронными оболочками он равен 0.
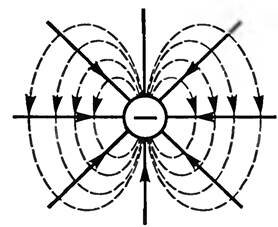
Кроме орбитального магнитного момента, электрон обладает еще собственным (спиновым) магнитным моментом \(~\vec p_{ms}\), что впервые установили О. Штерн и В. Герлах в 1922 г. Существование магнитного поля у электрона было объяснено его вращением вокруг собственной оси, хотя и не следует буквально уподоблять электрон вращающемуся заряженному шарику (волчку).
Достоверно установлено, что магнитное поле электрона является таким же неотъемлемым свойством, как его масса и заряд. Электрон, в весьма грубом приближении, можно представить как очень маленький шарик, окруженный электрическим и магнитным полями (рис. 2). Магнитные поля у всех электронов одинаковы, как одинаковы их массы и заряды. Спиновый магнитный момент \(~\vec p_{ms}\) — вектор, направленный вдоль оси вращения. Он может ориентироваться только двумя способами: либо по..., либо против... Если в том месте, где находится электрон, есть внешнее магнитное поле, то либо по полю, либо против поля. Как показано в квантовой физике, в одинаковом энергетическом состоянии могут находиться только два электрона, спиновые магнитные моменты которых противоположны (принцип Паули).
У многоэлектронных атомов спиновые магнитные моменты отдельных электронов, как и орбитальные моменты, складываются как векторы. При этом результирующий спиновый магнитный момент атома у атомов с заполненными электронными оболочками равен 0.
Общий магнитный момент атома (молекулы) \(~\vec p_a\) равен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов:
Диамагнетики состоят из атомов, которые в отсутствие внешнего магнитного поля не имеют собственных магнитных моментов, так как у них скомпенсированы все спиновые и все орбитальные магнитные моменты.
Внешнее магнитное поле не действует на весь атом диамагнетика, но действует на отдельные электроны атома, магнитные моменты которых отличны от нуля. Пусть в данный момент скорость \(~\vec v\) электрона составляет некоторый угол α (рис. 3) с магнитной индукцией \(~\vec B_0\) внешнего поля.
Благодаря составляющей \(~\vec v_{\perp}\) на электрон будет действовать сила Лоренца \(~F_L\) (направленная к нам на рис. 3), которая вызовет дополнительное (кроме других движений, в которых участвует электрон при отсутствии поля) движение по окружности. Но это движение представляет собой дополнительный круговой ток, который создаст магнитное поле, характеризуемое магнитным моментом \(~\vec p_m \)(наведенным), направленным по правилу правого винта навстречу \(~\vec B_0\) . В результате диамагнетики ослабляют внешнее магнитное поле.
Парамагнетики состоят из атомов, у которых результирующий магнитный момент атома \(~\vec p_a \not = 0\). В отсутствие внешнего поля эти моменты ориентированы хаотически и вещество в целом не создает вокруг себя магнитного поля. При помещении парамагнетиков в магнитное поле происходит преимущественная ориентация векторов \(~\vec p_a\) по полю (этому препятствует тепловое движение частиц). Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным. При ослаблении внешнего магнитного поля до нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамагнетик размагничивается. В парамагнетиках наблюдается и диамагнитный эффект, но он значительно слабее парамагнитного.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C.330- 332.