SA. Поверхностное натяжение

Поверхностная энергия

Наиболее характерным свойством жидкости, отличающим ее от газа, является то, что на границе с газом жидкость образует свободную поверхность, наличие которой приводит к возникновению явлений особого рода, называемых поверхностными. Своим возникновением они обязаны особым физическим условиям, в которых находятся молекулы вблизи свободной поверхности.

На каждую молекулу жидкости действуют силы притяжения со стороны окружающих ее молекул, расположенных от нее на расстоянии порядка 10^-9 м (радиус молекулярного действия). На молекулу M₁, расположенную внутри жидкости (рис. 1), действуют силы со стороны таких же молекул, и равнодействующая этих сил близка к нулю.

Рис. 1

Для молекул M₂ равнодействующие сил отличны от нуля и направлены внутрь жидкости, перпендикулярно к ее поверхности. Таким образом, все молекулы жидкости, находящиеся в поверхностном слое, втягиваются внутрь жидкости. Но пространство внутри жидкости занято другими молекулами, поэтому поверхностный слой создает давление на жидкость (молекулярное давление).

Чтобы переместить молекулу M₃, расположенную непосредственно под поверхностным слоем, на поверхность, необходимо совершить работу против сил молекулярного давления. Следовательно, молекулы поверхностного слоя жидкости обладают дополнительной потенциальной энергией по сравнению с молекулами внутри жидкости. Эту энергию называют поверхностной энергией.

Очевидно, что величина поверхностной энергии тем больше, чем больше площадь свободной поверхности. Пусть площадь свободной поверхности изменилась на ΔS, при этом поверхностная энергия изменилась на \(~\Delta W_p = \sigma \cdot \Delta S\), где σ — коэффициент поверхностного натяжения. Так как для этого изменения необходимо совершить работу

\(~A = \Delta W_p ,\) то \(~A = \sigma \cdot \Delta S .\)

Отсюда \(~\sigma = \dfrac{A}{\Delta S}\) .

Единицей коэффициента поверхностного натяжения в СИ является джоуль на квадратный метр (Дж/м²).

Коэффициент поверхностного натяжения — величина, численно равная работе, совершенной молекулярными силами при изменении площади свободной поверхности жидкости на 1 м² при постоянной температуре .

Так как любая система, предоставленная сама себе, стремится занять такое положение, в котором ее потенциальная энергия наименьшая, то жидкость обнаруживает стремление к сокращению свободной поверхности. Поверхностный слой жидкости ведет себя подобно растянутой резиновой пленке, т.е. все время стремится сократить площадь своей поверхности до минимальных размеров, возможных при данном объеме.

Например, капля жидкости в состоянии невесомости имеет сферическую форму.

Поверхностное натяжение

Свойство поверхности жидкости сокращаться можно истолковать как существование сил, стремящихся сократить эту поверхность. Молекула M₁ (рис. 2), расположенная на поверхности жидкости, взаимодействует не только с молекулами, находящимися внутри жидкости, но и с молекулами, находящимися на поверхности жидкости, расположенными в пределах сферы молекулярного действия. Для молекулы M₁ равнодействующая \(~\vec R\) молекулярных сил, направленных вдоль свободной поверхности жидкости, равна нулю, а для молекулы M₂, расположенной у границы поверхности жидкости, \(~\vec R \ne 0\) и \(~\vec R\) направлена по нормали к границам свободной поверхности и по касательной к самой поверхности жидкости.

Рис. 2

Равнодействующая сил, действующих на все молекулы, находящиеся на границе свободной поверхности, и есть сила поверхностного натяжения. В целом она действует так, что стремится сократить поверхность жидкости.

Можно предположить, что сила поверхностного натяжения \(~\vec F\) прямо пропорциональна длине l границы поверхностного слоя жидкости, ведь на всех участках поверхностного слоя жидкости молекулы находятся в одинаковых условиях:

\(~F \sim l .\)

Действительно, рассмотрим вертикальный прямоугольный каркас (рис. 3, а, б), подвижная сторона которого уравновешена. После извлечения рамки из раствора мыльной пленки подвижная часть перемещается из положения 1 в положение 2. Учитывая, что пленка представляет собой тонкий слой жидкости и имеет две свободные поверхности, найдем работу, совершаемую при перемещении поперечины на расстояние h = a₁ ⋅ a₂: A = 2F⋅h, где F — сила, действующая на каркас со стороны каждого поверхностного слоя. С другой стороны, \(~A = \sigma \cdot \Delta S = \sigma \cdot 2l \cdot h\).

Рис. 3

Следовательно, \(~2F \cdot h = \sigma \cdot 2l \cdot h \Rightarrow F = \sigma \cdot l\), откуда \(~\sigma = \dfrac Fl\).

Согласно этой формуле единицей коэффициента поверхностного натяжения в СИ является ньютон на метр (Н/м).

Коэффициент поверхностного натяжения σ численно равен силе поверхностного натяжения, действующей на единицу длины границы свободной поверхности жидкости. Коэффициент поверхностного натяжения зависит от природы жидкости, от температуры и от наличия примесей. При увеличении температуры он уменьшается.

• При критической температуре, когда исчезает различие между жидкостью и паром, σ = 0.

Примеси в основном уменьшают (некоторые увеличивают) коэффициент поверхностного натяжения.

Таким образом, поверхностный слой жидкости представляет собой как бы эластичную растянутую пленку, охватывающую всю жидкость и стремящуюся собрать ее в одну «каплю». Такая модель (эластичная растянутая пленка) позволяет определять направление сил поверхностного натяжения. Например, если пленка под действием внешних сил растягивается, то сила поверхностного натяжения будет направлена вдоль поверхности жидкости против растяжения. Однако это состояние существенно отличается от натяжения упругой резиновой пленки. Упругая пленка растягивается за счет увеличения расстояния между частицами, при этом сила натяжения возрастает, при растяжении же жидкой пленки расстояние между частицами не меняется, а увеличение поверхности достигается в результате перехода молекул из толщи жидкости в поверхностный слой. Поэтому при увеличении поверхности жидкости сила поверхностного натяжения не изменяется (она не зависит от площади поверхности).

См. также

1. Кикоин А.К. О силах поверхностного натяжения // Квант. — 1983. — № 12. — С. 27-28

Смачивание

В случае соприкосновения с твердым телом силы сцепления молекул жидкости с молекулами твердого тела начинают играть существенную роль. Поведение жидкости будет зависеть от того, что больше: сцепление между молекулами жидкости или сцепление молекул жидкости с молекулами твердого тела.

Смачивание — явление, возникающее вследствие взаимодействия молекул жидкости с молекулами твердых тел. Если силы притяжения между молекулами жидкости и твердого тела больше сил притяжения между молекулами жидкости, то жидкость называют смачивающей; если силы притяжения жидкости и твердого тела меньше сил притяжения между молекулами жидкости, то жидкость называют несмачивающей это тело.

Одна и та же жидкость может быть смачивающей и несмачивающей по отношению к разным телам. Так, вода смачивает стекло и не смачивает жирную поверхность, ртуть не смачивает стекло, а смачивает медь.

Смачивание или несмачивание жидкостью стенок сосуда, в котором она находится, влияет на форму свободной поверхности жидкости в сосуде. Если большое количество жидкости налито в сосуд, то форма ее поверхности определяется силой тяжести, которая обеспечивает плоскую и горизонтальную поверхность. Однако у самых стенок явление смачивания и несмачивания приводят к искривлению поверхности жидкости, так называемые краевые эффекты.

Количественной характеристикой краевых эффектов служит краевой угол θ - угол между плоскостью касательной к поверхности жидкости и поверхностью твердого тела. Внутри краевого угла всегда находится жидкость (рис. 4, а, б). При смачивании он будет острым (рис. 4, а), а при несмачивании – тупым (рис. 4, б). В школьном курсе физики рассматривают только полное смачивание (θ = 0º) или полное несмачивание (θ = 180º).

Рис. 4

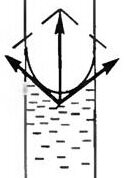
Силы, связанные с наличием поверхностного натяжения и направленные по касательной к поверхности жидкости, в случае выпуклой поверхности дают результирующую, направленную внутрь жидкости (рис. 5, а). В случае вогнутой поверхности результирующая сила направлена, наоборот, в сторону газа, граничащего с жидкостью (рис. 5, б).

Рис. 5.

Если смачивающая жидкость находится на открытой поверхности твердого тела (рис. 6, а), то происходит ее растекание по этой поверхности. Если на открытой поверхности твердого тела находится несмачивающая жидкость, то она принимает форму, близкую к шаровой (рис. 6, б).

Рис. 6

Смачивание имеет важное значение как в быту, так и в промышленности. Хорошее смачивание необходимо при крашении, стирке, обработке фотоматериалов, нанесении лакокрасочных покрытий, при склеивании материалов, при пайке, во флотационных процессах (обогащение руд ценной породой). И наоборот, при сооружении гидроизоляционных устройств необходимы материалы, не смачиваемые водой.

Капиллярные явления

Искривление поверхности жидкости у краев сосуда особенно отчетливо видно в узких трубках, где искривляется вся свободная поверхность жидкости. В трубках с узким сечением эта поверхность представляет собой часть сферы, ее называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 7, а), а у несмачивающей — выпуклый (рис. 7, б). Так как площадь поверхности мениска больше, чем площадь поперечного сечения трубки, то под действием молекулярных сил искривленная поверхность жидкости стремится выпрямиться.

Рис. 7

Силы поверхностного натяжения создают дополнительное (лапласово) давление под искривленной поверхностью жидкости.

Если поверхность жидкости вогнутая, то сила поверхностного натяжения направлена из жидкости (рис. 8, а), и давление под вогнутой поверхностью жидкости меньше, чем под плоской, на \(~p = \dfrac{2 \sigma }{R}\). Если поверхность жидкости выпуклая, то сила поверхностного натяжения направлена внутрь жидкости (рис. 8, б), и давление под выпуклой поверхностью жидкости больше, чем под плоской, на ту же величину.

• 

  а
• 

  б

Рис. 8

• Эта формула является частным случаем формулы Лапласа, определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:

\(~p = \sigma \cdot \left( \dfrac{1}{R_1} + \dfrac{1}{R_2} \right),\)

где R₁ и R₂ — радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости. Для цилиндрической поверхности (R₁ = l; R₂ = ∞) избыточное давление \(~p = \dfrac{\sigma}{R}\) .

Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в широкий сосуд, то вследствие наличия силы лапласова давления жидкость в капилляре поднимается (если жидкость смачивающая) или опускается (если жидкость несмачивающая) (рис. 9, а, б), так как под плоской поверхностью жидкости в широком сосуде избыточного давления нет.

Рис. 9

Явления изменения высоты уровня жидкости в капиллярах по сравнению с уровнем жидкости в широких сосудах называются капиллярными явлениями.

Жидкость в капилляре поднимается или опускается на такую высоту h, при которой сила гидростатического давления столба жидкости уравновешивается силой избыточного давления, т.е.

\(~\dfrac{2 \sigma}{R} = \rho \cdot g \cdot h .\)

Откуда \(~h = \dfrac{2 \sigma}{\rho \cdot g \cdot R}\). Если смачивание не полное θ ≠ 0 (θ ≠ 180°), то, как показывают расчеты, \(~h = \dfrac{2 \sigma}{\rho \cdot g \cdot R} \cdot \cos \theta\).

Капиллярные явления весьма распространены. Поднятие воды в почве, система кровеносных сосудов в легких, корневая система у растений, фитиль и промокательная бумага — капиллярные системы.

Литература

1. Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 178-184.
2. Википедия
3. Открытая Физика