SA. Магнитное поле

Немного геометрии

Вспомним названия направлений на плоскости γ (рис. 1): OC — «вправо», OB — «вниз», OD — «влево», OA — «вверх».

• 

  Рис. 1
• 

  Рис. 2

Примечание. Все направления указаны относительно плоскости (листа), расположенной вертикально.

Но указанных направлений на плоскости будет недостаточно, т.к. необходимо указывать еще и направления в пространстве. Например, направление вектора, который расположен перпендикулярно плоскости γ. Поэтому введем еще два направления: «к нам» — если вектор выходит из плоскости в нашу сторону, «от нас» — если вектор входит в плоскость. Например, на рис. 2 направление тока в проводнике FE, расположенного перпендикулярно плоскости γ, может быть OE — «к нам» или OF — «от нас».

Для изображения векторов, перпендикулярных плоскости рисунка применяют условные обозначения: крестики (как оперение стрелки, улетающей от вас) и точки (как наконечник стрелы, летящей к вам).

Например: а) по проводнику течет ток (рис. 3), б) в данной области существует однородное магнитное поле с вектором магнитной индукции \(~\vec B\) (рис. 4).

• 

  Рис. 3
• 

  Рис. 4

Тогда в плоскости γ направление векторов будем изображать так, как на рисунках 5 (окружности на данном рисунке — это сечения проводника) и 6.

• 

  Рис. 5
• 

  Рис. 6

Немного истории

Уже в VI в. до н.э. в Китае было известно, что некоторые руды, например, магнитный железняк, обладают способностью притягиваться друг к другу и притягивать на расстоянии железные предметы. Поскольку впервые куски таких руд были обнаружены возле города Магнезии в Малой Азии, то в Древней Греции они получили название магнитов.

Термин «полюсы магнитов» от греческого слова περαζ — ось, конец оси был введен Петром Перегрином в 1269 г. в книге «Письма о магнитах».

Явления притяжения разноименных и отталкивания одноименных полюсов магнита напоминают явления взаимодействия разноименных и одноименных электрических зарядов. Однако многочисленные попытки ученых установить связь между электрическими и магнитными явлениями на протяжении многих столетий оставались безрезультатными.

Наступает 1820 год. В феврале секретарь Датского королевского общества Ханс Кристиан Эрстед (1777-1851) прямо во время лекции обнаружил, что магнитная стрелка отклоняется, если пропустить ток по проводнику, и возвращается в свое первоначальное положение при размыкании цепи (рис. 7).

Рис. 7

Описание этого простого опыта произвело сильное впечатление в научном сообществе и вызвало лавину новых открытий. Жан Батист Био и Феликс Савар нашли выражение для силы, действующей со стороны тока на магнитный полюс. Доминик Франсуа Араго обнаружил намагничивание железных опилок проводником с током. Андре Мари Ампер показал (сентябрь 1820 г.), что два параллельных проводника с токами притягиваются или отталкиваются в зависимости от направления тока в них (рис. 8, а, б), а так же получил выражение для силы взаимодействия между электрическими токами и выявил тесную «генетическую» связь между электрическими и магнитными процессами. В декабре 1821 года М. Фарадей демонстрирует первый электромотор.

Таким образом, родилась новая область физики — электродинамика.

Рис. 8

См. так же

1. Васильев А. Вольта, Эрстед, Фарадей //Квант. — 2000. — № 5. — С. 16-17
2. Слободянюк А.И. Физика 10. §12. Постоянное магнитное поле

Магнитное поле

Впервые термин «Магнитное поле» ввел в 1845 М. Фарадей, классическая теория электромагнитного поля была создана Дж. Максвеллом (1873), квантовая теория — в 20-х годах 20 века.

• Магнитное поле — это особый вид материи, посредством которой осуществляется взаимодействие между движущимися заряженными частицами.

Перечислим основные свойства магнитного поля, полученные из экспериментов (они частично повторяют свойства электрического поля):

1. Оно материально, т.е. существует независимо от наших знаний о нем.
2. Порождается только движущимся электрическим зарядом: вокруг любого движущегося заряженного тела существует магнитное поле.

   Магнитное поле может быть создано и магнитом, но и там, причиной появления поля является движение электронов.

   Магнитное поле может быть создано и переменным электрическим полем.

3. Обнаружить это поле можно по действию на движущийся электрический заряд (или проводник с током) с некоторой силой.
4. Это поле распространяется в пространстве с конечной скоростью, равной скорости света в вакууме.

Для силовой характеристики магнитного поля был введен вектор индукции магнитного поля \(~\vec B\).

• Модуль вектора индукции магнитного поля можно определить как отношение максимальной силы F_max, с которой магнитное поле действует на проводник единичной длины (l = 1 м), к силе тока I в проводнике:

\(B = \dfrac{F_{max}}{I \cdot l}.\)

В СИ единицей индукции магнитного поля является 1 Тл (Тесла):

1 Тл = 1 Н/(1 А ⋅ 1 м).

Для магнитного поля, так же как и для электрического, справедлив принцип суперпозиции:

• если магнитное поле в данной точке пространства создается несколькими движущимися зарядами, то индукция результирующего поля равна векторной сумме индукций полей, созданных каждым движущимся зарядом:

\(~\vec B = \vec B_1 + \vec B_2 + \ldots + \vec B_n.\)

Графически магнитные поля изображаются с помощью специальных линий, называемых линиями индукции магнитного поля. Касательная к любой линии в каждой точке направлены вдоль вектора индукции магнитного поля \(~\vec B\). Свойства линий индукции, с одной стороны, сходны со свойствами силовых линий электростатического поля — они не пересекаются, не прерываются, густота линий больше там, где модуль вектора \(~\vec B\) больше. С другой стороны есть отличия — линии индукции магнитного поля всегда замкнуты, т.е. магнитное поле является вихревым.

Направление вектора индукции

Для определения направления вектора индукции магнитного поля, созданного магнитами, используют свободную магнитную стрелку (воображаемую):

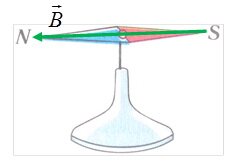
• вектор индукции магнитного поля \(~\vec B\) направлен от южного S полюса стрелки (свободно вращающейся в магнитном поле) к северному N (рис. 9).

Рис. 9

Например, чтобы определить направление вектора индукции магнитного поля между двумя полюсами магнитов в точке А (рис. 10, а), поместим в данную точку магнитную стрелку. К северному N полюсу магнита повернется южный S полюс стрелки, к южному S полюсу магнита — северный N полюс стрелки (рис. 10, б). Так как вектор индукции магнитного поля направлен от южного S полюса стрелки к северному N, то вектор \(~\vec B\) будет направлен вправо (рис. 10, в).

• 

  а
• 

  б
• 

  в

Рис. 10

Для определения направления вектора индукции магнитного поля \(~\vec B\) проводника с током применяют правило буравчика или правило правой руки:

а) для прямого проводника с током правило правой руки имеет следующий вид:

• большой палец правой руки, отставленный на 90°, направляем по току I, тогда четыре согнутых пальца, обхватывающие проводник, укажут направление вектора индукции магнитного поля \(~\vec B\)(рис. 11).

б) для витка (катушки) с током правило правой руки имеет следующий вид:

• четыре согнутых пальца правой руки, обхватывающей виток (катушку), направляем по току I, тогда большой палец, отставленный на 90°, укажет направление вектора индукции магнитного поля \(~\vec B\) в центре витка (рис. 12).

• 

  Рис. 11
• 

  Рис. 12

Примеры магнитных полей

Для решения задач важно знать формулы, которые описывают магнитные поля, создаваемые проводниками с токами различных конфигураций.

Модуль индукции магнитного поля бесконечного прямолинейного проводника с током силой I на расстоянии r от проводника в вакууме (рис. 13) определяется по формуле

\(~B = \dfrac{\mu_0 \cdot I}{2 \pi \cdot r}\),

где μ₀ – магнитная постоянная, равная 4π·10^-7 Тл·м/А .

Модуль индукции магнитного поля в центре тонкого кругового витка (кольца) радиуса R (рис. 14), по которому протекает ток силой I равен

\(~B = \dfrac{\mu_0 \cdot I}{2R}\).

Модуль индукции магнитного поля в середине катушки (соленоида) с током I (рис. 15) определяется по формуле

\(~B = \dfrac{\mu_0 \cdot I \cdot N}{l}\) ,

где N — число витков катушки, l — длина катушки.

• 

  Рис. 13
• 

  Рис. 14
• 

  Рис. 15

Литература

Жилко, В. В. Физика: учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. обучения с 12-летним сроком обучения (базовый и повышенный уровни) /В. В. Жилко, Л. Г. Маркович. — 2-е изд., исправленное. — Минск: Нар. асвета, 2008. — С. 147-157.