SA. Газовые законы

Изопроцессы в идеальном газе

Для описания состояния газа достаточно задать три макроскопических параметра — объем V, давление p и температуру T. Изменение одного из этих параметров вызывает изменение остальных. Если одновременно меняются объем, давление и температура, то на опыте трудно установить какие-либо закономерности. Проще сначала рассмотреть газ неизменной массы (m = const), зафиксировать значение одного из макропараметров (V, p или T) и рассмотреть изменение при этом двух других.

Процессы, при которых один из параметров p, V или Τ остается постоянным при данной массе газа, называют изопроцессами.

• isos в переводе с греческого означает «равный».

Законы, описывающие изопроцессы в идеальном газе, были открыты экспериментально.

Изотермический процесс

Изотермический процесс — это изопроцесс, происходящий при постоянной температуре: Τ = const.

• therme — тепло.

Закон экспериментально открыли независимо друг от друга английский химик и физик Роберт Бойль (1662) и французский физик Эдм Мариотт (1676).

Закон изотермического процесса (Бойля-Мариотта): для данной массы газа при постоянной температуре произведение давления на объем есть величина постоянная:

\(~p \cdot V = \operatorname{const}\) или для двух состояний \(~p_1 \cdot V_1 = p_2 \cdot V_2 .\)

Для осуществления изотермического процесса надо сосуд, наполненный газом, привести в контакт с термостатом.

• Термостат — это прибор для поддержания постоянной температуры. Подробнее см. wikipedia

• Изотермическим процессом приближенно можно считать процесс медленного сжатия или расширения газа в сосуде с поршнем. Термостатом в этом случае служит окружающая среда.

Изобарный процесс

Изобарный процесс — это изопроцесс, происходящий при постоянном давлении: p = const.

• baros — тяжесть, вес.

Закон экспериментально исследовали независимо друг от друга французские физики Жак Шарль (1787) и Жозеф Гей-Люссак (1802).

• Работа Ж. Шарля была опубликована уже после открытия Ж. Гей-Люссака. Но изобарный процесс в российских учебниках называют законом Гей-Люссака, в белорусских — законом Шарля.

Закон изобарного процесса: при данной массе газа при постоянном давлении отношение объема к абсолютной температуре есть величина постоянная:

\(~\dfrac{V}{T} = \operatorname{const},\) или \(~\dfrac{V_1}{T_1} = \dfrac{V_2}{T_2} .\)

Этот закон можно записать через температуру t, измеряемую по шкале Цельсия\[~V = V_0 \cdot (1 + \alpha \cdot t),\] где V₀ — объем газа при 0 °С, α = 1/273 К^-1 — температурный коэффициент объемного расширения.

• Опыт показывает, что при малых плотностях температурный коэффициент объемного расширения не зависит от вида газа, т.е. одинаков для всех газов).

Получить изобарный процесс можно при помощи цилиндра с невесомым поршнем.

Изохорный процесс

Изохорный процесс — это изопроцесс, происходящий при постоянном объеме: V = const.

• chora — занимаемое место, объем.

Закон экспериментально исследовали независимо друг от друга французские физики Жак Шарль (1787) и Жозеф Гей-Люссак (1802).

• Изохорный процесс в российских учебниках называют законом Шарля, в белорусских — законом Гей-Люссака.

Закон изохорного процесса: при данной массе газа при постоянном объеме отношение давления к абсолютной температуре есть величина постоянная:

\(~\dfrac{p}{T} = \operatorname{const}\), или \(~\dfrac{p_1}{T_1} = \dfrac{p_2}{T_2} .\)

Если температуру измерять по шкале Цельсия, то закон Гей-Люссака запишется в виде\[~p = p_0 \cdot (1 + \alpha \cdot t),\] где p₀ — давление газа при 0 °С, α — температурный коэффициент давления, оказавшийся одинаковым для всех газов: α = 1/273 К^-1 .

Получить изохорный процесс можно в баллоне, который не изменяет свой объем при данном изменении температуры.

Тщательная экспериментальная проверка современными методами показала, что уравнение состояния идеального газа и вытекающие из него законы Бойля-Мариотта, Гей-Люссака и Шарля достаточно точно описывают поведение реальных газов при небольших давлениях и не слишком низких температурах.

Немного математики

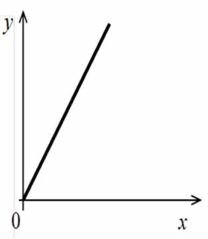
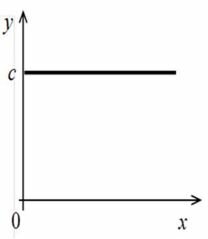
График функции y(x), где a, b и с — постоянные величины:

• y = a⋅x — прямая линия, проходящая через начало координат (рис. 1, а);
• y = c — прямая, перпендикулярная оси y и проходящая через точку c координатой y = c (рис. 1, б);
• \(~y = \dfrac{b}{x} \) — гипербола (рис. 1, в).

• 

  а
• 

  б
• 

  в

Рис. 1

Графики изопроцессов

Так как мы рассматриваем три макропараметра p, T и V, то возможно три системы координат: (p, V), (V, Τ), (p, Т).

Графики зависимости между параметрами данной массы при постоянной температуре называются изотермами.

Рассмотрим два изотермических процесса с температурами T₁ и T₂ (T₂ > T₁). В координатах, где есть ось температуры ((V, Τ) и (p, Т)), графиками будут прямые, перпендикулярные оси T, и проходящие через точки T₁ и T₂ (рис. 2, а, б).

Определим вид графика в осях (p, V). Для изотермического процесса \(~p \cdot V = \operatorname{const}\). Обозначим эту константу буквой z₁. Тогда

\(~p \cdot V = z_1\) или \(~p = \dfrac{z_1}{V}\).

График этой функции — гипербола (рис. 2, в).

• 

  а
• 

  б
• 

  в

Рис. 2

Графики зависимости между параметрами газа при постоянной массе газа и давлении называют изобарами.

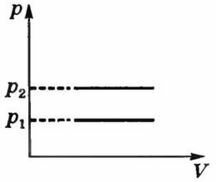
Рассмотрим два изобарных процесса с давлениями p₁ и p₂ (p₂ > p₁). В координатах, где есть ось давления ((p, Τ) и (p, V)), графиками будут прямые, перпендикулярные оси p, и проходящие через точки p₁ и p₂ (рис. 3, а, б).

Определим вид графика в осях (V, T). Для изобарного процесса \(~\dfrac{V}{T} = \operatorname{const}\). Обозначим эту константу буквой z₂. Тогда

\(~\dfrac{V}{T} = z_2\) или \(~V = z_2 \cdot T\).

График этой функции — прямая линия, проходящая через начало координат (рис. 3, в).

• 

  а
• 

  б
• 

  в

Рис. 3

Графики зависимости между параметрами газа при постоянной массе газа и постоянном объеме называют изохорами.

Рассмотрим два изохорных процесса с объемами V₁ и V₂ (V₂ > V₁). В координатах, где есть ось объема ((V, Τ) и (p, V)), графиками будут прямые, перпендикулярные оси V, и проходящие через точки V₁ и V₂ (рис. 4, а, б).

Определим вид графика в осях (p, T). Для изохорного процесса \(~\dfrac{p}{T} = \operatorname{const}\). Обозначим эту константу буквой z₃. Тогда

\(~\dfrac{p}{T} = z_3\) или \(~p = z_3 \cdot T\).

График этой функции — прямая линия, проходящая через начало координат (рис. 4, в).

• 

  а
• 

  б
• 

  в

Рис. 4

• Все графики изопроцессов прямые линии (исключение, гипербола в осях p(V)). Эти прямые проходят или через нуль, или перпендикулярно одной из осей.
• Так как давление газа, его объем и температура не могут равняться нулю, то при приближении к нулевым значениям линии графика изображают пунктирными линиями.

Уравнение состояния идеального газа

В изопроцессах два параметра изменялись при постоянном значении третьего. Но возможны случаи, когда меняются сразу три параметра. Например, когда нагретый у поверхности Земли воздух поднимается вверх, то он расширяется, давление его уменьшается и температура понижается.

Уравнение, связывающее температуру T, давление p и объем V для данной массы идеального газа , называют уравнением состояния газа.

Это уравнение было получено экспериментально, но его можно вывести из основного уравнения MKT:

\(~p = n \cdot k \cdot T.\)

По определению концентрация газа

\(~n = \dfrac NV,\)

где N — число молекул. Тогда

\(~p = \dfrac NV \cdot k \cdot T \Rightarrow \dfrac{p \cdot V}{T} = k \cdot N . \qquad (1)\)

При неизменной массе газа число молекул в нем постоянно и произведение \(~k \cdot N = \operatorname{const}.\) Следовательно,

\(~\dfrac{p \cdot V}{T} = \operatorname{const}\) или для двух состояний \(~\dfrac{p_1 \cdot V_1}{T_1} = \dfrac{p_2 \cdot V_2}{T_2} . \qquad (2)\)

Соотношение (2) и есть уравнение состояния идеального газа. Его называют уравнением Клапейрона. Им пользуются в тех случаях, когда масса газа и его химический состав не изменяются и нужно сравнить два состояния газа.

Уравнение Клапейрона-Менделеева

В уравнении (1) число молекул N можно выразить через постоянную Авогадро \(~N = \dfrac mM \cdot N_A\), где m — масса газа, Μ — его молярная масса. Тогда получаем \(~\dfrac{p \cdot V}{T} = \dfrac mM \cdot k \cdot N_A \Rightarrow\)

\(~p \cdot V = \dfrac mM \cdot R \cdot T . \qquad (3)\)

Здесь \(~R = k \cdot N_A\) — универсальная газовая постоянная, равная

R = 1,38·10^-23 Дж/К · 6,02·10²³ моль^-1 = 8,31 Дж/(моль·К).

Уравнение (3) — это тоже уравнение состояния идеального газа. В такой форме оно было впервые записано русским ученым Д.И.Менделеевым, поэтому его называют уравнением Клапейрона-Менделеева. Оно справедливо для любой массы газа и связывает между собой параметры одного состояния газа.

Законы Авогадро и Дальтона

Из уравнения состояния вытекают два следствия:

1. Из формулы (1) получим \(~N = \dfrac{p \cdot V}{k \cdot T}\), откуда видно, что если различные газы занимают при одинаковых температурах и одинаковых давлениях равные объемы, то число N молекул у них тоже одинаково, т.е. вытекает установленный опытным путем закон Авогадро: при равных давлениях и температурах в одинаковых объемах любых газов содержится одинаковое число молекул.
2. Пусть в сосуде имеется смесь газов, каждый из которых при отсутствии других оказывает соответственно давление p₁, p₂, ... (парциальные давления газов). Запишем для каждого газа уравнение состояния:
   \(~p_1 \cdot V = N_1 \cdot k\cdot T, p_2 \cdot V = N_2 \cdot k \cdot T, \ldots\)
   и сложим их:
   \(~p_1+ p_2 + \ldots = \dfrac{(N_1+ N_2 + \ldots) \cdot k \cdot T}{V} = \dfrac{N \cdot k \cdot T}{V},\)
   где N₁ + N₂ + ... = N — число молекул смеси газов. Но \(~\dfrac{N \cdot k \cdot T}{V} = p\) .
   Следовательно, p = p₁ + p₂ + ..., т.е давление смеси газов равно сумме парциальных давлений каждого из газов — это закон Дальтона, открытый им в 1801 г. экспериментально.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 143-146.