Referat. Самоиндукция

Самоиндукция

Явление самоиндукции

Если по катушке идет переменный ток, то магнитный поток, пронизы-вающий катушку, меняется. Поэтому возникает ЭДС индукции в том же самом проводнике, по которому идет переменный ток. Это явление называют самоиндукцией.

При самоиндукции проводящий контур играет двоякую роль: по нему протекает ток, вызывающий индукцию, и в нем же появляется ЭДС индукции. Изменяющееся магнитное поле индуцирует ЭДС в том самом проводнике, по которому течет ток, создающий это поле.

В момент нарастания тока напряженность вихревого электрического поля в соответствии с правилом Ленца направлена против тока. Следовательно, в этот момент вихревое поле препятствует нарастанию тока. Наоборот, в момент уменьшения тока вихревое поле поддерживает его.

Это приводит к тому, что при замыкании цепи, содержащей источник постоянной ЭДС, определенное значение силы тока устанавливается не сразу, а постепенно с течением времени (рис. 9). С другой стороны, при отключении источника ток в замкнутых контурах прекращается не мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника, так как изменение тока и его магнитного поля при отключении источника происходит очень быстро.

Рис. 9

Явление самоиндукции можно наблюдать на простых опытах. На рисунке 10 показана схема параллельного включения двух одинаковых ламп. Одну из них подключают к источнику через резистор R, а другую — последовательно с катушкой L с железным сердечником. При замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием. ЭДС самоиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения.

Рис. 10

Появление ЭДС самоиндукции при размыкании можно наблюдать на опыте с цепью, схематически показанной на рисунке 11. При размыкании ключа в катушке L возникает ЭДС самоиндукции, поддерживающая первоначальный ток. В результате в момент размыкания через гальванометр течет ток (штриховая стрелка), направленный против начального тока до размыкания (сплошная стрелка). Причем сила тока при размыкании цепи превосходит силу тока, проходящего через гальванометр при замкнутом ключе. Это означает, что ЭДС самоиндукции E_is больше ЭДС E батареи элементов.

Рис. 11

Индуктивность

Величина магнитной индукции B, создаваемой током в любом замкнутом контуре, пропорциональна силе тока. Так как магнитный поток Ф пропорционален В, то можно утверждать, что

\(~\Phi = L \cdot I\) ,

где L – коэффициент пропорциональности между током в проводящем контуре и созданным им магнитным потоком, пронизывающим этот контур. Величину L называют индуктивностью контура или его коэффициентом самоиндукции.

Используя закон электромагнитной индукции, получим равенство:

\(~E_{is} = - \frac{\Delta \Phi}{\Delta t} = - L \cdot \frac{\Delta I}{\Delta t}\) ,

если считать, что форма контура остается неизменной и поток меняется только за счет изменения тока.

Из полученной формулы следует, что

индуктивность – это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

Индуктивность подобно электроемкости, зависит от геометрических факторов: размеров проводника и его формы, но не зависит непосредственно от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.

Единицу индуктивности в СИ называют генри (Гн). Индуктивность проводника равна 1 Гн, если в нем при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В:

1 Гн = 1 В / (1 А/с) = 1 В·с/А = 1 Ом·с

Энергия магнитного поля

Найдем энергию, которой обладает электрический ток в проводнике. Согласно закону сохранения энергии энергия тока равна той энергии, которую должен затратить источник тока (гальванический элемент, генератор на электростанции и др.) на создание тока. При прекращении тока эта энергия выделяется в той или иной форме.

Энергия тока, о которой сейчас пойдет речь, совсем иной природы, чем энергия, выделяемая постоянным током в цепи в виде теплоты, количество которой определяется законом Джоуля-Ленца.

При замыкании цепи, содержащей источник постоянной ЭДС, энергия источника тока первоначально расходуется на создание тока, т. е. на приведение в движение электронов проводника и образование связанного с током магнитного поля, а также отчасти на увеличение внутренней энергии проводника, т.е. на его нагревание. После того как установится постоянное значение силы тока, энергия источника расходуется исключительно на выделение теплоты. Энергия тока при этом уже не изменяется.

Выясним теперь, почему же для создания тока необходимо затратить энергию, т.е. необходимо совершить работу. Объясняется это тем, что при замыкании цепи, когда ток начинает нарастать, в проводнике появляется вихревое электрическое поле, действующее против того электрического поля, которое создается в проводнике благодаря источнику тока. Для того чтобы сила тока стала равной I, источник тока должен совершить работу против сил вихревого поля. Эта работа и идет на увеличение энергии тока. Вихревое поле совершает отрицательную работу.

При размыкании цепи ток исчезает и вихревое поле совершает положительную работу. Запасенная током энергия выделяется. Это обнаруживается по мощной искре, возникающей при размыкании цепи с большой индуктивностью.

Найдем выражение для энергии тока I, текущего по цепи с индуктивностью L.

Работа А, совершаемая источником с ЭДС E за малое время Δt, равна:

\(~A = E \cdot I \cdot \Delta t\) . (1)

Согласно закону сохранения энергии эта работа равна сумме приращения энергии тока ΔW_m и количества выделяемой теплоты \(~Q = I^2 \cdot R \cdot \Delta t\):

\(~A = \Delta W_m + Q\) . (2)

Отсюда приращение энергии тока

\(~\Delta W_m = A - Q = I \cdot \Delta t \cdot (E - I \cdot R)\) . (3)

Согласно закону Ома для полной цепи

\(~I \cdot R = E + E_{is}\) . (4)

где \(~E_{is} = - L \cdot \frac{\Delta I}{\Delta t}\) — ЭДС самоиндукции. Заменяя в уравнении (3) произведение I∙R его значением (4), получим:

\(~\Delta W_m = I \cdot \Delta t \cdot (E - E - E_{is}) = - E_{is} \cdot I \cdot \Delta t = L \cdot I \cdot \Delta I\) . (5)

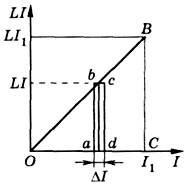
На графике зависимости L∙I от I (рис. 12) приращение энергии ΔW_m численно равно площади прямоугольника abcd со сторонами L∙I и ΔI. Полное изменение энергии при возрастании тока от нуля до I₁ численно равно площади треугольника ОВС со сторонами I₁ и L∙I₁. Следовательно,

\(~W_m = \frac{L \cdot I^2_1}{2}\) .

Рис. 12

Энергия тока I, текущего по цепи с индуктивностью L, равна

\(~W_m = \frac{L \cdot I^2}{2}\) .

Энергию магнитного поля, заключенную в единице объема пространства, занятого полем, называют объемной плотностью энергии магнитного поля ω_m:

\(~\omega_m = \frac{W_m}{V}\) .

Если магнитное поле создано внутри соленоида длиной l и площадью витка S, тогда, учитывая, что индуктивность соленоида \(~L = \frac{\mu_0 \cdot N^2 \cdot S}{l}\) и модуль вектора индукции магнитного поля внутри соленоида \(~B = \frac{\mu_0 \cdot N \cdot I}{l}\) , получаем

\(~I = \frac{B \cdot l}{\mu_0 \cdot N} ; W_m = \frac{L \cdot I^2}{2} = \frac{1}{2} \cdot \frac{\mu_0 \cdot N^2 \cdot S}{l} \cdot \left (\frac{B \cdot l}{\mu_0 \cdot N} \right )^2 = \frac{B^2}{2 \cdot \mu_0} \cdot S \cdot l\) .

Так как V = S∙l, то плотность энергии магнитного поля

\(~\omega_m = \frac{B^2}{2 \cdot \mu_0}\) .

Магнитное поле, созданное электрическим током, обладает энергией, прямо пропорциональной квадрату силы тока. Плотность энергии магнитного поля пропорциональна квадрату магнитной индукции.

Литература

1. Жилко В.В. Физика: Учеб. пособие для 10-го кл. общеобразоват. шк. с рус. яз. обучения / В.В. Жилко, А.В. Лавриненко, Л.Г. Маркович. – Мн.: Нар. асвета, 2001. – 319 с.
2. Мякишев, Г.Я. Физика : Электродинамика. 10-11 кл. : учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. – М.: Дрофа, 2005. – 476 с.

Составители

Хомченко Е. (11 «А» МГОЛ № 1, 2008 г.)