Referat. Закон сохранения энергии

Механическая энергия

Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.

Для характеристики различных форм движения материи вводятся соответствующие виды энергии, например: механическая, внутренняя, энергия электростатических, внутриядерных взаимодействий и др.

Энергия подчиняется закону сохранения, который является одним из важнейших законов природы.

Механическая энергия Е характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Она равна сумме кинетической и потенциальной энергий.

Кинетическая энергия

Рассмотрим случай, когда на тело массой m действует постоянная сила \(~\vec F\) (она может быть равнодействующей нескольких сил) и векторы силы \(~\vec F\) и перемещения \(~\vec s\) направлены вдоль одной прямой в одну сторону. В этом случае работу силы можно определить как A = F∙s. Модуль силы по второму закону Ньютона равен F = m∙a, а модуль перемещения s при равноускоренном прямолинейном движении связан с модулями начальной υ₁ и конечной υ₂ скорости и ускорения а выражением \(~s = \frac{\upsilon^2_2 - \upsilon^2_1}{2a}\) .

Отсюда для работы получаем

\(~A = F \cdot s = m \cdot a \cdot \frac{\upsilon^2_2 - \upsilon^2_1}{2a} = \frac{m \cdot \upsilon^2_2}{2} - \frac{m \cdot \upsilon^2_1}{2}\) . (1)

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела.

Кинетическая энергия обозначается буквой E_k.

\(~E_k = \frac{m \cdot \upsilon^2}{2}\) . (2)

Тогда равенство (1) можно записать в таком виде:

\(~A = E_{k2} - E_{k1}\) . (3)

Теорема о кинетической энергии

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

Если начальная скорость движения тела массой m равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела:

\(~A = E_{k2} - E_{k1}= \frac{m \cdot \upsilon^2}{2} - 0 = \frac{m \cdot \upsilon^2}{2}\) . (4)

Физический смысл кинетической энергии

кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.

Потенциальная энергия

Потенциальная энергия – это энергия взаимодействия тел.

Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Потенциальными называются силы, работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.

При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.

Силы, работа которых зависит от формы траектории, называются непотенциальными. При перемещении материальной точки или тела по замкнутой траектории работа непотенциальной силы не равна нулю.

Потенциальная энергия взаимодействия тела с Землей

Найдем работу, совершаемую силой тяжести F_т при перемещении тела массой m вертикально вниз с высоты h₁ над поверхностью Земли до высоты h₂ (рис. 1). Если разность h₁ – h₂ пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести F_т во время движения тела можно считать постоянной и равной mg.

Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна

\(~A = F \cdot s = m \cdot g \cdot (h_1 - h_2)\) . (5)

Рис. 1

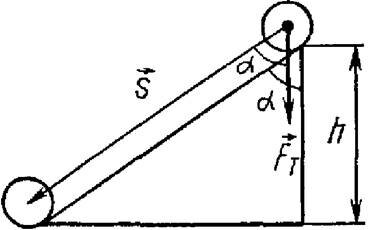
Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести F_т = m∙g совершает работу

\(~A = m \cdot g \cdot s \cdot \cos \alpha = m \cdot g \cdot h\) , (6)

где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.

Рис. 2

Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотами h’, h’’ и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:

\(~A = m \cdot g \cdot h' + m \cdot g \cdot h'' + \ldots + m \cdot g \cdot h^n = m \cdot g \cdot (h' + h'' + \ldots + h^n) = m \cdot g \cdot (h_1 - h_2)\) , (7)

где h₁ и h₂ – высоты от поверхности Земли, на которых расположены соответственно точки В и С.

Рис. 3

Равенство (7) показывает, что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.

При движении вниз работа силы тяжести положительна, при движении вверх – отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.

Равенство (7) можно представить в таком виде:

\(~A = - (m \cdot g \cdot h_2 - m \cdot g \cdot h_1)\) . (8)

Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.

Работа силы тяжести при перемещении тела массой m из точки, расположенной на высоте h₂, в точку, расположенную на высоте h₁ от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.

\(~A = - (E_{p2} - E_{p1})\) . (9)

Потенциальная энергия обозначается буквой Е_p.

Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.

При таком выборе нулевого уровня потенциальная энергия Е_p тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:

\(~E_p = m \cdot g \cdot h\) . (10)

Физический смысл потенциальной энергии взаимодействия тела с Землей

потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.

В отличие от кинетической энергии поступательного движения, которая может иметь лишь положительные значения, потенциальная энергия тела может быть как положительной, так и отрицательной. Тело массой m, находящееся на высоте h, где h < h₀ (h₀ – нулевая высота), обладает отрицательной потенциальной энергией:

\(~E_p = -m \cdot g \cdot h\) .

Потенциальная энергия гравитационного взаимодействия

Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами m и М, находящихся на расстоянии r одна от другой, равна

\(~E_p = G \cdot \frac{M \cdot m}{r}\) . (11)

где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е_p = 0) принят при r = ∞.

Потенциальная энергия гравитационного взаимодействия тела массой m с Землей, где h – высота тела над поверхностью Земли, M_e – масса Земли, R_e – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.

\(~E_e = G \cdot \frac{M_e \cdot m \cdot h}{R_e \cdot (R_e +h)}\) . (12)

При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой m с Землей для малых высот h (h « R_e) равна

\(~E_p = m \cdot g \cdot h\) ,

где \(~g = G \cdot \frac{M_e}{R^2_e}\) – модуль ускорения свободного падения вблизи поверхности Земли.

Потенциальная энергия упруго деформированного тела

Вычислим работу, совершаемую силой упругости при изменении деформации (удлинения) пружины от некоторого начального значения x₁ до конечного значения x₂ (рис. 4, б, в).

Рис. 4

Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т.к. сила упругости линейно зависит от x) и умножить на модуль перемещения:

\(~A = F_{upr-cp} \cdot (x_1 - x_2)\) , (13)

где \(~F_{upr-cp} = k \cdot \frac{x_1 - x_2}{2}\) . Отсюда

\(~A = k \cdot \frac{x_1 - x_2}{2} \cdot (x_1 - x_2) = k \cdot \frac{x^2_1 - x^2_2}{2}\) или \(~A = -\left(\frac{k \cdot x^2_2}{2} - \frac{k \cdot x^2_1}{2} \right)\) . (14)

Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:

\(~E_p = \frac{k \cdot x^2}{2}\) . (15)

Из формул (14) и (15) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:

\(~A = -(E_{p2} - E_{p1})\) . (16)

Если x₂ = 0 и x₁ = х, то, как видно из формул (14) и (15),

\(~E_p = A\) .

Физический смысл потенциальной энергии деформированного тела

потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.

Закон сохранения энергии в механических процессах

Потенциальная энергия характеризует взаимодействующие тела, а кинетическая энергия – движущиеся тела. И потенциальная, и кинетическая энергия изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля. Рассмотрим вопрос об изменениях энергии при взаимодействиях тел, образующих замкнутую систему.

Замкнутая система – это система, на которую не действуют внешние силы или действие этих сил скомпенсировано. Если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии тел, взятому с противоположным знаком:

\(~A = -(E_{p2} - E_{p1})\) . (17)

По теореме о кинетической энергии, работа тех же сил равна изменению кинетической энергии:

\(~A = E_{k2} - E_{k1}\) . (18)

Из сравнения равенств (17) и (18) видно, что изменение кинетической энергии тел в замкнутой системе равно по абсолютному значению изменению потенциальной энергии системы тел и противоположно ему по знаку:

\(~E_{k2} - E_{k1} = -(E_{p2} - E_{p1})\) или \(~E_{k1} + E_{p1} = E_{k2} + E_{p2}\) . (19)

Закон сохранения энергии в механических процессах:

сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и си-лами упругости, остается постоянной.

Сумма кинетической и потенциальной энергии тел называется полной механической энергией.

Основное содержание закона сохранения энергии заключается не только в установлении факта сохранения полной механической энергии, но и в установлении возможности взаимных превращений кинетической и потенциальной энергии тел в равной количественной мере при взаимодействии тел.

Приведем простейший опыт. Подбросим вверх стальной шарик. Сообщив начальную скорость υ_нач, мы придадим ему кинетическую энергию, из-за чего он начнет подниматься вверх. Действие силы тяжести приводит к уменьшению скорости шарика, а значит, и его кинетической энергии. Но шарик поднимается выше и выше и приобретает все больше и больше потенциальной энергии (Е_p = m∙g∙h). Таким образом, кинетическая энергия не исчезает бесследно, а происходит ее превращение в потенциальную энергию.

В момент достижения верхней точки траектории (υ = 0) шарик полностью лишается кинетической энергии (Е_k = 0), но при этом его потенциальная энергия становится максимальной. Дальше шарик меняет направление движения и с увеличивающейся скоростью движется вниз. Теперь происходит обратное превращение потенциальной энергии в кинетическую.

Закон сохранения энергии раскрывает физический смысл понятия работы:

работа сил тяготения и сил упругости, с одной стороны, равна увеличению кинетической энергии, а с другой стороны, – уменьшению потенциальной энергии тел. Следовательно, работа равна энергии, превратившейся из одного вида в другой.

Закон об изменении механической энергии

Если система взаимодействующих тел не замкнута, то ее механическая энергия не сохраняется. Изменение механической энергии такой системы равно работе внешних сил:

\(~A_{vn} = \Delta E = E - E_0\) . (20)

где Е и Е₀ – полные механические энергии системы в конечном и начальном состояниях соответственно.

Примером такой системы может служить система, в которой наряду с потенциальными силами действуют непотенциальные силы. К непотенциальным силам относятся силы трения. В большинстве случаев, когда угол между силой трения F_tr и элементарным перемещением Δr тела составляет π радиан, работа силы трения отрицательна и равна

\(~A_{tr} = -F_{tr} \cdot s_{12}\) ,

где s₁₂ – путь тела между точками 1 и 2.

Силы трения при движении системы уменьшают ее кинетическую энергию. В результате этого механическая энергия замкнутой неконсервативной системы всегда уменьшается, переходя в энергию немеханических форм движения.

Например, автомобиль, двигавшийся по горизонтальному участку дороги, после выключения двигателя проходит некоторый путь и под действием сил трения останавливается. Кинетическая энергия поступательного движения автомобиля стала равной нулю, а потенциальная энергия не увеличилась. Во время торможения автомобиля произошло нагревание тормозных колодок, шин автомобиля и асфальта. Следовательно, в результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.

Закон сохранения и превращения энергии

при любых физических взаимодействиях энергия превращается из одной формы в другую.

Иногда угол между силой трения F_tr и элементарным перемещением Δr равен нулю и работа силы трения положительна:

\(~A_{tr} = F_{tr} \cdot s_{12}\) ,

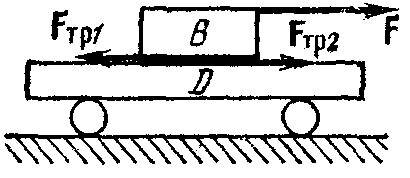
Пример 1. Пусть, внешняя сила F действует на брусок В, который может скользить по тележке D (рис. 5). Если тележка перемещается вправо, то работа силы трения скольжения F_tr2, действующей на тележку со стороны бруска, положительна:

Рис. 5

Пример 2. При качении колеса его сила трения качения направлена вдоль движения, так как точка соприкосновения колеса с горизонтальной поверхностью двигается в направлении, противоположном направлению движения колеса, и работа силы трения положительна (рис. 6):

Рис. 6

Литература

1. Кабардин О.Ф. Физика: Справ. материалы: Учеб. пособие для учащихся. – М.: Просвещение, 1991. – 367 с.
2. Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Про-свещение, 1992. – 191 с.
3. Элементарный учебник физики: Учеб. пособие. В 3 т. / Под ред. Г.С. Ландсберга: т. 1. Механика. Теплота. Молекулярная физика. – М.: Физматлит, 2004. – 608 с.
4. Яворский Б.М., Селезнев Ю.А. Справочное руководство по физике для поступающих в вузы и самообразования. – М.: Наука, 1983. – 383 с.

Составители

Варахобова Анна (11 «А», МГОЛ № 1, 2008 г.)