Kvant. Эффективное напряжение

Ланге В. Эффективное напряжение в сети переменного тока //Квант. — 2001. — № 3. — С. 40-41.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Перспективность использования электрической энергии в технике и быту стала очевидной еще в начале XIX века, а в конце его началась настоящая война между сторонниками постоянного и переменного тока. В ней, однако, не было ни победителей, ни побежденных, так как для одних целей оказывается необходимым постоянный ток (например, при электролизе), в других случаях целесообразнее использовать переменный (в особенности, при передаче электроэнергии на большие расстояния). Уместно напомнить, что сейчас существуют простые установки, позволяющие легко преобразовывать один вид тока в другой.

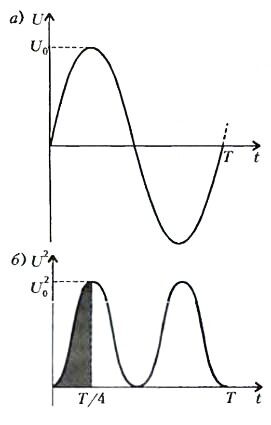
В соответствии с названием, в сетях постоянного тока напряжение остается неизменным, а в сетях переменного тока оно со временем меняется. Обычно изменение напряжения происходит по синусоидальному закону \(~U = U_0 \sin \omega t\), где ω - циклическая частота, связанная с периодом Т соотношением \(~\omega = \frac{2\pi}{T}\), a U₀ — амплитудное значение напряжения. Графически характер изменения напряжения со временем показан на рисунке 1,а.

Рис. 1

Предположим, что необходимо рассчитать мощность Р, которую будет потреблять из сети переменного тока с амплитудным напряжением U₀ электрическая печь, имеющая сопротивление R. Как известно, такие расчеты выполняются с помощью закона Джоуля-Ленца:

\(~P = I^2 R\) ,

или в нашем случае

\(~P = \frac{U^2}{R}\) .

Однако в рассматриваемой цепи напряжение меняется и по знаку, и по величине. Как учесть эти два обстоятельства?

Начнем с ответа на более простой первый вопрос. В законе Джоуля-Ленца фигурирует квадрат напряжения, а поскольку (+U)² = (-U)² , тепловыделение не зависит от знака разности потенциалов (или, что то же, от направления тока). Стало быть, и в сети переменного тока электрическая печь будет исправно выполнять свое назначение.

Попробуем теперь ответить на вопрос, какое напряжение надо подставить в формулу закона Джоуля-Ленца, чтобы получить правильное значение мощности в случае переменного тока. Для этого рассчитаем количество теплоты, выделяемое переменным током за время, равное периоду. И сделаем это следующим образом.

Поскольку теплоотдача определяется квадратом напряжения, легко понять, что тепловыделение имеет период \(~\frac T2\) (рис. 1,б). Более того, достаточно рассмотреть интервал от 0 до \(~\frac T4\), так как выделенная на рисунке фигура, если учесть ее зеркальные отражения, повторяется именно с таким периодом. На этом интервале фаза колебаний меняется от φ₁ = 0 до \(~\varphi_2 = \frac{\pi}{4}\).

Запишем выражение для мощности электропечи в некоторый момент времени t:

\(~P(t) = \frac{U^2}{R} = \frac{U^2_0}{R} \sin^2 \omega t\) .

Ее среднее значение <Р> в интервале времени от 0 до \(~\frac T4\) представим в виде

\(~

= <\frac{U^2_0}{R} \sin^2 \omega t> = \frac{U^2_0}{R} <\sin^2 \omega t>\) .</center>

<center>Рис. 2</center>

В угловых скобках остался зависящий от времени сомножитель, обозначаемый далее буквой y. Для расчета его среднего значения воспользуемся рисунком 2, отметив на оси абсцисс точки E₁, Е и E₂, соответствующие фазам \(~\frac{\pi}{4} - \alpha\), \(~\frac{\pi}{4}\) и \(~\frac{\pi}{4} + \alpha\), где α - произвольный угол, удовлетворяющий условию \(~0 < \alpha < \frac{\pi}{4}\). Ясно, что

<center>\(~E_1C_1 = \sin^2 \left( \frac{\pi}{4} - \alpha \right) = \cos^2 \left( \frac{\pi}{2} - \left( \frac{\pi}{4} - \alpha \right)\right) = \cos^2 \left( \frac{\pi}{4} + \alpha \right) = 1 - \sin^2 \left( \frac{\pi}{4} + \alpha \right) = 1 - C_2E_2\) .</center>

Таким образом, кривая 0С₁СС₂В делит прямоугольник 0DBA на две равные части, каждая площадью

<center>\(~\frac{A0 \cdot 0D}{2} = \frac{\frac{\pi}{2} \cdot 1}{2} = \frac{\pi}{4}\) .</center>

Чтобы найти среднее значение \(~\sin^2 \omega t\) за время изменения фазы от 0 до \(~\frac{\pi}{2}\), нужно площадь криволинейной фигуры 0СВА разделить на ее основание:

<center>\(~<\sin^2 \omega t> = \frac{\frac{\pi}{4}}{\frac{\pi}{2}} = \frac 12\) .</center>

После этого находим среднее значение мощности за время от t₁ = 0 до \(~t_2 = \frac T4\) :

<center>\(~<P> = \frac{U^2_0}{R} <\sin^2 \omega t> = \frac{U^2_0}{2R}\) .</center>

Поскольку такой же результат можно получить для каждого из последующих интервалов длительностью \(~\frac T4\) правая часть формулы дает мощность плитки сопротивлением R, включенной в сеть переменного тока с амплитудным значением напряжения U₀.

Пусть эта же плитка включена в сеть постоянного тока с таким напряжением U_ef, что ее мощность осталась прежней. Тогда, приравнивая мощность плитки в сети постоянного тока

<center>\(~P = \frac{U^2_{ef}}{R}\) .</center>

правой части предыдущего выражения, после несложного преобразования получим

<center>\(~U_{ef} = \frac{U_0}{\sqrt 2}\) .</center>

Напряжение в сети постоянного тока, где плитка дает такой же тепловой эффект, как и в сети переменного тока с амплитудным значением напряжения, в \(~\sqrt 2\) большим, называется эффективным (или действующим) напряжением в сети переменного тока. В обычной городской еети амплитудное напряжение составляет приблизительно 310 В. Тогда для эффективного напряжения получается хорошо знакомое число 220 В.

Заметим, что аналогичное соотношение связывает эффективное и амплитудное значения и для силы тока в сети переменного тока.