Kvant. Электрические колебания
Кикоин А.К. Электрические колебания. Колебательный контур //Квант. — 1983. — № 11. — С. 29-30.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
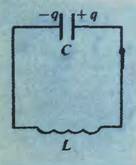
В 1853 году знаменитый английский физик Уильям Томсон, впоследствии лорд Кельвин, опубликовал статью под названием «О неустановившихся электрических токах». В ней он показал, что в контуре, составленном из конденсатора емкостью С и катушки с индуктивностью L (рис. 1), должны происходить электромагнитные колебания с периодом \(~T = 2 \pi \sqrt{LC}\).
При слове «колебания» нам сразу представляется образ колеблющегося математического маятника (рис. 2) или груза, прикрепленного к пружине (рис. 3). Но колебания означают не только механическое движение какого-нибудь тела «туда — сюда». Под колебаниями нужно понимать всякое периодическое изменение какой-либо величины, то есть такое изменение, при котором значение этой величины через определенный промежуток времени, называемый периодом колебаний, повторяется.
При механических колебаниях материальной точки периодически изменяющаяся величина — это координата x точки. В нашем контуре — это заряд q, который был сообщен обкладкам конденсатора. В течение периода колебаний заряд на обкладке постепенно исчезает, изменяет свой знак и снова восстанавливается. Совершает колебания и напряжение \(~U = \frac{q}{C}\) между обкладками конденсатора, и сила тока I в цепи, так как в любой момент времени справедливо соотношение
Колеблются также напряженность Е электрического поля в конденсаторе (потому что \(~E = \frac{U}{d}\), где d — расстояние между обкладками) и индукция В магнитного поля катушки (потому что она пропорциональна току).
Это аналогично тому, как при механических колебаниях периодически изменяется не только координата точки, но и ее скорость, ускорение, кинетическая энергия и т. д. Все эти величины совершают колебания.
В школьном учебнике «Физика 10» рассказывается об аналогии между механическими и электрическими колебаниями. Эту аналогию можно сделать более строгой, если заметить, что уравнение (1) по форме совпадает с уравнением, выражающим второй закон Ньютона для тела, колеблющегося под действием пружины:
где F — сила упругости, действующая на тело, m — масса, \(~\frac{\Delta \upsilon}{\Delta t} = a\) — ускорение тела. Поэтому уравнение (1) можно исследовать по принципу «одинаковые уравнения имеют одинаковые решения».
Сравнение уравнений (1) и (2) показывает, что напряжение U соответствует силе упругости F, ток I в катушке — скорости υ движения тела, а индуктивность катушки L — массе тела m. Наконец, из соотношений
следует, что величина, обратная емкости конденсатора (\(~\frac{1}{C}\)), соответствует жесткости пружины k. Сводная таблица, подытоживающая эту аналогию, приведена в «Физике 10».
В заключение рассмотрим интересный вопрос о токе в колебательном контуре. Несмотря на то, что контур разомкнут (между обкладками конденсатора нет проводников), по такой «разомкнутой цепи» течет ток. Более того, если бы сопротивление катушки и подводящих проводов было равно нулю (сверхпроводимость), электрический ток, вызванный разрядом конденсатора, никогда бы не прекратился.
Как это ни странно, но ток в колебательном контуре можно считать замкнутым. Чтобы это понять, нужно вернуться к явлению электромагнитной индукции. Как впервые указал Максвелл, сущность этого явления заключается не в том, что изменение магнитного потока порождает индукционный ток, а в том, что изменение магнитного поля порождает электрическое поле с замкнутыми силовыми линиями (вихревое поле). Индукционный ток — это движение заряженных частиц в этом поле. В связи с такой формулировкой явления электромагнитной индукции Максвеллу пришла в голову гениальная мысль, что должно существовать и обратное явление: изменяющееся электрическое поле создает магнитное поле.
В нашем колебательном контуре, когда в нем происходят колебания, есть место, где ничего, кроме изменяющегося электрического поля, нет.. Это конденсатор. Значит, вокруг конденсатора существует магнитное поле (рис. 4). С другой стороны, известно, что магнитное поле окружает всякий электрический ток. Выходит, что своим свойством быть окруженным магнитным полем изменяющееся (переменное) электрическое поле ничем не отличается от электрического тока. Со времен Максвелла скорость изменения переменного электрического поля и называют поэтому током, точнее, током смещения.
Таким образом, можно считать, что «обычный» электрический ток (так называемый ток проводимости) в проводящей части цепи колебательного контура как бы продолжается в конденсаторе током без зарядов — током смещения.