Kvant. Экономия топлива

Стасенко А.Л. Экономия топлива на Луне //Квант. — 1994. — № 1. — С. 35-36.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Просверление луны колоссальным буравом — вот что служило предметом речи мистера Лунда!.. Близко уже то время, когда луна украсится дырой. Дыра будет принадлежать англичанам» (Антон Чехов).

Рис. 1 и 2

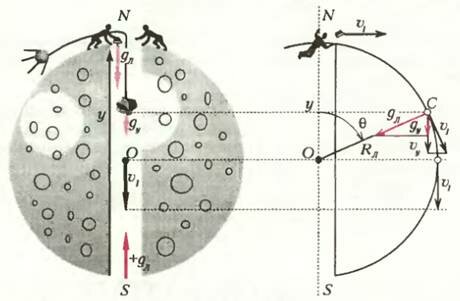
Не может быть, чтобы из такой грандиозной дыры и нам нельзя было бы извлечь какой-нибудь пользы. Для начала уроним (т.е. просто отпустим) какой-нибудь Предмет, например Утюг, в эту шахту, проходящую прямо через центр Луны (рис. 1). У самой поверхности, в точке N, сила, действующая на Утюг, будет равна mg_L, где m — масса Утюга, g_L — ускорение тяготения на Луне (оно приблизительно в 6 раз меньше земного). Но когда Утюг будет пролетать центр Луны (точка O), очевидно, что сила тяготения станет равной нулю (если, конечно, считать Луну строго сферически симметричной) — в этой точке уравновесятся силы тяготения, порожденные всеми элементами объема Луны. Значит, в момент прохождения центра скорость Утюга перестанет расти, а при дальнейшем движении начнет уменьшаться. Интуитивно ясно, что в точке S, диаметрально противоположной точке N, Утюг затормозится до нулевой скорости — ведь воздуха на Луне нет, а стенок шахты он пусть не касается, значит, нет никаких потерь энергии. Далее, если Утюг в точке S никто не схватит, то он снова начнет двигаться к центру, вновь вернется в точку N ит.д. Это колебательное движение может продолжаться вечно.

Из всего сказанного отметим, что у поверхности Луны ускорение равно по модулю g_L, в центре — нулю; значит, оно как-то изменяется по радиусу. Но как? Простейшая зависимость — линейная, (это пока что только предположение), т.е.

\(~g_y = g_L \frac{y}{R_L}\) . (1)

Теперь бросим тот же Утюг вдоль поверхности (другими словами, горизонтально, тангенциально, или по касательной) , но так, чтобы он снова смог попасть в точку S (рис. 2). Для этого ему нужно сообщить скорость спутника υ_I. Напомним, что ее можно найти, приравняв ускорение тяготения (его значение постоянно во всех точках на поверхности сферического тела) центростремительному\[~g_L = \frac{\upsilon^2_I}{R_L}\] , откуда

\(~\upsilon_I = \sqrt{g_L R_L}\) . (2)

Это — первая космическая скорость, о чем и говорит индекс «I». Подчеркнем, что хотя величина скорости Утюга во всех точках траектории (окружности) одинакова, тем не менее это движение с ускорением, поскольку вектор скорости изменяется (поворачивается).

Пусть в некоторый момент времени t Утюг находится в точке С окружности, имеющей угловую координату θ (полярный угол) и, следовательно, отстоящей отточки 6росания N (здесь t = 0, θ = 0) на расстоянии υ_It, измеренном по дуге. Спроектируем все кинематические характеристики Утюга в этой точке (радиус-вектор \(~\vec R_L\), скорость \(~\vec \upsilon_I\), ускорение \(~\vec g_L\)) на ось шахты SN (ось Y). Получим (см. рис. 2)

\(~y = R_L \cos \theta\) , (3) \(~\upsilon_y = -\upsilon_I \sin \theta\) , (4) \(~g_y = -g_L \cos \theta\) . (5)

Заметим, что центральный угол θ измеряется длиной дуги окружности, деленной на ее радиус\[~\theta = \frac{\upsilon_I t}{R_L}\]. Из равенств (3) и (5) получаем формулу для g_y, в точности совпадающую с (1). Но это опять-таки не доказательство, а лишь намек на действительное изменение тяжести тела внутри шахты.

Ясно, что если проекции ускорения, скорости и координаты тела, движущегося по окружности, на диаметр в точности равны соответствующим характеристикам движения вдоль самого диаметра, то оба Утюга (брошенный в N вдоль поверхности и уроненный в шахту) достигнут диаметрально противоположной точки S одновременно. Так же одновременно они и вернутся в начальную точку N. Но это если верна зависимость (1). В действительности она верна в случае однородной планеты, во всех точках которой плотность постоянна.

Над этим фактом в последние триста лет размышляли многие классики точных наук. Современный школьник, можно сказать, с детства знает, что шар массой М и радиусом r притягивает тело массой m, находящееся на его поверхности, с силой Ньютона \(~F = G \frac{Mm}{r^2}\), т.е. так, как если бы вся масса шара была сосредоточена в его центре. Подставив сюда \(~M = \frac 43 \pi r^3 \rho_0\) (ρ₀ — плотность, одинаковая по объему шара), получим

\(~F = mg = mG \frac 43 \pi \rho_0 \frac{r^3}{r^2}\) ,

откуда

\(~g(r) = \frac 43 G \pi \rho_0 r\) ,

т.е. ускорение действительно пропорционально расстоянию от центра. Самым важным здесь является то, что масса шарового слоя, лежащего «над» поверхностью r = const, не влияет на силу (и ускорение) тяготения. Вспомним, что великий Ньютон на девять лет задержал издание своих « Начал», пока не доказал эти факты.

Итак, выражение (3), а именно

\(~y = R_L \cos \frac{\upsilon_I t}{R_L}\)

является «расписанием» движения Утюга в лунной диаметральной шахте. Это — уравнение так называемого гармонического колебания (рис. 3, сплошная линия).

Рис. 3

А скорость, согласно равенству (4), будет изменяться по закону

\(~\upsilon_y = -\upsilon_I \sin \frac{\upsilon_I t}{R_L}\)

и, значит, будет достигать наибольшей величины в те моменты времени, в которые у = 0, т.е. в центре планеты (см. рис. 3, штриховая линия).

Нам важно, что в центре Луны оброненный в шахту Утюг достигнет скорости спутника. И тут вдумчивого школьника должна осенить мысль: зачем же Утюгу без дела болтаться от полюса к полюсу? Нельзя ли в связи с подорожанием топлива использовать для его экономии работу поля, тяготения?

Возьмем вместо Утюга Очень Большую Скалу и привяжем к ней невесомую нерастяжимую нить длиной R_L, другой конец которой прикрепим к спутнику или космическому кораблю (см. рис. 1). Падая в шахту, Большая Скала будет ускорять вдоль поверхности Луны (пусть без трения) космический корабль. Когда Скала будет пролетать центр Луны, корабль окажется над шахтой и его можно отцепить от нити, а так как оба тела имеют одну и ту же скорость υ_I, то корабль полетит дальше по орбите спутника, а Скала — к противоположному полюсу S, где к ней можно будет быстро (ее скорость на мгновение станет равной нулю) привязать нить другого спутника. И таким образом Скала будет колебаться в шахте не бесполезно, а запуская на орбиту все новые и новые тела, при этом экономя много топлива, которое на Луне особенно дорого.

Но это все в предположении о том, что масса Скалы много больше масс ускоряемых тел и нитей — чтобы подчеркнуть это, мы и пишем Очень Большую Скалу с заглавных букв.

Пойдем дальше. Из равенств (3) и (4) получим

\(~\cos \theta = \frac{y}{R_L}, \sin \theta = \frac{\upsilon_y}{\upsilon_I}\) .

Возведем в квадрат и сложим:

\(~\left(\frac{\upsilon_y}{\upsilon_I} \right)^2 + \left(\frac{y}{R_L} \right)^2 = \sin^2 \theta + \cos^2 \theta = 1\) .

Разделив последнее уравнение на 2 и учитывая выражение (2) для υ_I, перепишем его в виде

\(~\frac{\upsilon^2_y}{2} + \frac 12 \frac{g_L y^2}{R_L} = \frac{\upsilon^2_I}{2} = \frac{g_L R_L}{2}\) .

Но ведь это не что иное как закон сохранения энергии, записанный, правда, для единичной массы. Первое слагаемое в левой части — кинетическая энергия на расстоянии у от центра, второе, следовательно, — потенциальная энергия. А их сумма — постоянная величина, которую можно записать либо в виде кинетической энергии в центре Луны (где потенциальная энергия принята за нуль), либо в виде потенциальной энергии у входа в шахту (где скорость, а значит, и кинетическая энергия, равна нулю).

Итак, потенциальная энергия тела массой m на расстоянии у от центра Луны записывается в виде \(~\frac{mg_L y^2}{2 R_L} = \frac{mg_y y}{2}\). Заметим, что для тела, брошенного вертикально над поверхностью Земли на высоту у, закон сохранения энергии мы записали бы в виде

\(~\frac{m \upsilon^2}{2} + mg_0 y = \frac{m \upsilon^2_0}{2} = m g_0 y_{max}\) ,

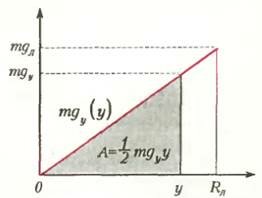
где υ₀ — скорость бросания, y_max - максимально достижимая высота. Здесь потенциальная энергия равна mg₀y, т.е. работе, которую надо совершить против постоянной силы тяготения mg₀ на перемещении y. В случае же падения в шахту сила тяжести — переменная (см. выражение (1)), поэтому для получения работы надо не только умножить mg_y на у, но еще разделить на 2 — ведь работа это площадь заштрихованного треугольника на рисунке 4.

Рис. 4

Ну, а если скала не настолько Большая, чтоб ее писать с заглавной буквы, т.е. если ее масса сравнима с массой корабля и массой нити-троса? Тогда закон сохранения (6) нужно переписать с учетом энергий этих масс. Попробуйте это сделать сами перед сном. Нужно только иметь в виду, что по мере опускания Скалы к центру Луны в шахту будет свешиваться все больший кусок троса, и он тоже, будучи теперь весомым, будет способствовать ускорению.