Kvant. Чайник-таймер

Стасенко А.Л. Как чайник стал таймером //Квант. — 2001. — № 5. — С. 36-37.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

timer: 1) хронометрист (на скачках); 2) часы, хронометр;

3) автоматический прибор, регулирующий продолжительность операции.

Англо-русский словарь

Не было часов у студента: счастливые их не наблюдают. Однако надо же знать - когда лекция, когда ужин... И тут пришло в голову Студенту использовать изменение со временем какой-нибудь физической величины, например температуры... чайника. А для этого пригодится лабораторный термометр, с помощью которого можно измерять температуру в пределах 0 °С < Т < 100 °С.

Итак, «заведем» такие часы: нагреем воду в чайнике до 100 °С, укутаем его одеялом (чтобы часы дольше работали) и вставим в носик термометр (рис.1).

Рис. 1

Теперь нужно часы проградуировать - найти взаимно однозначное соответствие между временем t и показаниями термометра Т (рис.2).

Рис. 2

Оценим прежде всего характерное время τ, за которое температура чайника заметно изменится. Почему он вообще остывает? Ясно, что это связано с наличием разности между температурой чайника Т, зависящей от времени, и температурой окружающего воздуха T_∞, которая, в общем, тоже может изменяться, но мы будем считать ее постоянной.

Если эта разность температур существует в точках пространства, отстоящих друг от друга на расстояние h, то плотность потока тепла q (энергию, уходящую в единицу времени через единицу площади) записывают в виде

\(~q = - \lambda \frac{T_{\infty} - T}{h}\) .

Собственно, это соотношение определяет величину λ - коэффициента теплопроводности материала, через который протекает тепловая энергия. Легко установить размерность этой величины:

[λ] = Дж/(м·с·К) = Вт/(м·К) .

В нашем случае это коэффициент теплопроводности одеяла (вместе с содержащимся в нем воздухом). А знак «минус» напоминает, что тепло течет в сторону уменьшения температуры.

Далее, если площадь поверхности чайника равна S, то полная энергия, уходящая через эту площадь в единицу времени, равна, очевидно, qS.

Осталось записать ясную физическую идею: вследствие отвода тепловой энергии температура воды в чайнике Т уменьшается. Если m - масса воды, c - ее удельная теплоемкость (теплоемкостью корпуса чайника и термометра пренебрежем), то

\(~\frac{mc \Delta T}{\Delta t} = -\frac{S\lambda}{h} (T - T_{\infty})\) .

Считая, что произведение mc постоянно, запишем это уравнение в так называемом релаксационном виде:

\(~\frac{\Delta T}{\Delta t} = -\frac{T - T_{\infty}}{\tau}\) , (*)

где величина

\(~\tau = \frac{hmc}{S\lambda}\) ,

просто обязана иметь размерность времени (проверьте).

Сделаем численную оценку этого времени. Будем считать для простоты, что чайник имеет форму шара радиусом a, заполненного водой. Тогда его поверхность S = 4πa² , масса воды в нем \(~m = \rho \cdot \frac 43 \pi a^3\) (где ρ - плотность воды), так что

\(~\tau = \frac{h\rho ac}{3\lambda}\) .

(В частности, отсюда видно, почему малышей нужно укутывать в три шубы особенно тщательно: поскольку их характерный размер a мал, нужно брать толщину шуб h побольше).

Итак, выпишем значения всех необходимых величин: плотность воды ρ = 103 кг/м³ , ее удельная теплоемкость c = 4,2·10³ Дж/(кг·К), коэффициент теплопроводности одеяла примем равным λ = 0,03 Вт/(м·К) (соответствующим хлопковой вате), его толщина пусть будет h = 3 см = 0,03 м, «радиус» чайника a ~ 0,1 м. Тогда

\(~\tau \sim \frac{3 \cdot 10^{-2} \cdot 10^3 \cdot 0,1 \cdot 4,2 \cdot 10^3}{3 \cdot 3 \cdot 10^{-2}}\) с = 1,4·10⁵ с ~ 40 ч.

Но что это за время? Если строго решить дифференциальное уравнение (*), получится экспоненциальная зависимость температуры от времени. Качественно она изображена на рисунке 2 сплошной линией. Характерное время τ получается при пересечении наклонной прямой, касательной к кривой T(t) в начальной точке T₀ = 100 °С, с прямой T_∞ = const (см. штриховые прямые на рисунке 2). Разумеется, если потребовать полного остывания (до нулевой разности температур: T - T_∞ → 0), то придется ждать бесконечно долго - таково уж свойство уравнения (*): наклон кривой \(~\frac{\Delta T}{\Delta t}\) уменьшается с уменьшением разности температур. Таким образом, для экспериментальной градуировки чайника как измерителя времени, вероятно, потребуются десятки часов. Конечно, это не значит, что придется не спать все это время, но все-таки нужно будет изредка вскакивать и сверять показания термометра с какими-то «эталонными часами» (взятыми на время у приятеля).

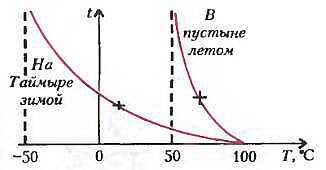
А теперь пора поговорить о «точности хода» нового таймера. Безусловно, температура будет определяться с некоторой ошибкой порядка минимального деления шкалы, например δT = 1 °С, - эта ошибка показана на рисунке 2 горизонтальным отрезком. Поскольку наклон кривой T(t) изменяется, будет расти ошибка определения соответствующих отрезков времени δt (принцип их построения ясен из рисунка). Значит, по мере остывания чайника часы будут давать все большую неопределенность во времени. Поэтому им разумно доверять, по-видимому, лишь в течение времени порядка τ, после чего рекомендуется «заводить» часы вновь (доводить воду до кипения). Понятно, что точность этих часов будет разной в жаркой пустыне и среди снегов. Этот факт иллюстрирует рисунок 3.

Рис. 3

Итак, спокойной ночи: следите за термометром!