Kvant. Хаос молекул и звезд

Стасенко А.Л. Хаос молекул и звезд //Квант. — 1998. — № 5. — С. 36-37

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Далеко-далеко в глубинах Вселенной живет большое звездное оолако, состоящее из одинаковых звезд типа нашего Солнца, которые летят равновероятно во всех направлениях с одинаковыми средними скоростями. И средние расстояния между ними тоже одинаковы. Физик сказал бы, что это похоже на однородный изотропный газ. А газ, как сказал бы древний грек, это же просто хаос (χαοζ).

Рис. 1

Однако звезды, согласно закону всемирного тяготения, взаимодействуют друг с другом. Пролетая одна вблизи другой, они не могут двигаться по прямой, их траектории искривляются, так что издалека кажется, что два упругих шарика столкнулись друг с другом и разлетелись под углом χ с прежней относительной скоростью (рис. 1). Но что произойдет с их планетными системами - это совсем небезразлично для их жителей. Для них важен вопрос, каково (хотя бы в среднем) время между столкновениями звезд в этом звездном облаке. И вообще: что такое «столкновение»? Ведь звезды взаимодействуют, в принципе, на любом расстоянии. (То же можно сказать о свободных электронах и протонах в газовой плазме. И даже нейтральные молекулы в «обычных» газах «чувствуют» друг друга издалека благодаря электромагнитным полям, порождаемым движением электронов (см., например, статью «Любовь и ненависть в мире молекул» в «Кванте» №2 за 1994 г.).

И тут пора написать несколько формул.

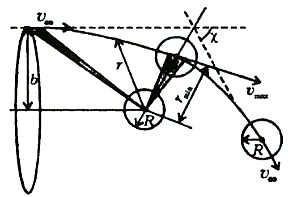
Пусть наименьшее допустимое расстояние между звездами равно r_min. Согласно второму закону Кеплера, площадь треугольника, «заметаемая» радиусом-вектором \(~\vec r\) в единицу времени, остается постоянной. Пусть относительная скорость звезд на большом удалении друг от друга равна \(~\upsilon_{\infty}\), так называемое прицельное расстояние равно b, а наибольшая скорость при наибольшем сближении равна υ_max. Запишем утверждение второго закона Кеплера для двух заштрихованных треугольников:

\(~\frac 12 b \upsilon_{\infty} \Delta t = \frac 12 r_{min} \upsilon_{max} \Delta t\) . (1)

Здесь b и r_min - высоты этих треугольников, a \(~\upsilon_{\infty} \Delta t\) и υ_maxΔt - их основания, т.е. расстояния, пройденные звездой за малое время Δt.

Ясно, что при сближении звезд их относительная скорость растет. За счет чего? Конечно, за счет работы силы притяжения \(~F = -G \frac{mm}{r^2}\). Это изменение скорости можно найти из второго закона Ньютона. А можно описать этот процесс на основе предположения о постоянстве суммарной механической энергии системы двух звезд. Иными словами, записать, что сумма их кинетической E_k и потенциальной E_p энергий одинакова при любом их расположении - например, при самом большом («бесконечном») и наименьшем расстояниях между ними:

\(~E_{k\ \infty} + 0 = E_{k\ max} + E_{p\ min}\) ,

или

\(~\frac{m \upsilon^2_{\infty}}{2} + 0 = \frac{m \upsilon^2_{max}}{2} + \left( -\frac{\alpha}{r_{min}}\right)\) . (2)

Здесь «ноль» (в левой части) означает, что при бесконечном удалении друг от друга зиезды не взаимодействуют, а слагаемое \(~-\frac{\alpha}{r_{min}}\) и правой части равно энергии их взаимодействия при r = r_min. Тут уместно вспомнить, что эта энергия взаимодействия (потенциальная энергия) как раз и равна работе, которую нужно затратить, чтобы «вытащить» на бесконечность одну звезду из потенциальной ямы, создаваемой другой звездой (рис.2). Поскольку сила притяжения обратно пропорциональна квадрату расстояния, работа против этой силы будет обратно пропорциональна первой степени расстояния, а коэффициент α, конечно же, содержит произведение масс звезд и гравитационную постоянную\[~\alpha = 2m^2G\].

Рис. 2

Внимательный читатель может спросить, почему здесь появился множитель «2». В механике известно, что движение двух взаимодействующих частиц (например, двух тел, соединенных одной пружинкой, двух гравитирующих масс, двух электрических зарядов) на расстоянии r можно свести к движению одной (так называемой приведенной) массы

\(~\frac m2 = \frac{m_1 m_2}{m_1 + m_2}\) ,

с радиусом-вектором \(~\vec r\). Поскольку нас интересуют здесь только оценки порядков величин, не будем останавливаться на этом подробнее.

Выразим υ_max из равенства (1) и подставим в (2). Тогда получим

\(~ \left(\frac{b}{r_{min}}\right)^2 = 1 + \frac{\alpha}{r_{min} m \upsilon^2_{\infty}}\) . (3)

Видно, что последнее слагаемое есть отношение потенциальной энергии взаимодействия звезд (при наибольшем сближении) к кинетической энергии их относительного движения. Если бы не было никакого взаимодействия (α = 0), то получилось бы b = r_min, что естественно, так как звезды при этом двигались бы по прямым. Значит, взаимодействие приводит к увеличению прицельного расстояния, а именно — все звезды, центры которых на бесконечности попадут в круг радиусом b, пройдут от нашей звезды не далее чем на расстоянии r_min (т.е. и этом смысле заведомо «столкнутся» с ней). Если среднее расстояние между звездами равно l, то концентрация звезд будет n = l^-3. Тогда «поток звезд» через круг с прицельным расстоянием b равен \(~\pi b^2 n \upsilon_{\infty}\) , и, значит, среднее время между столкновениями звезд будет

\(~\tau \sim \frac{1}{\pi b^2 n \upsilon_{\infty}} = \frac{l^3}{\pi b^2 \upsilon_{\infty}}\) . (4)

Сделаем теперь численные оценки. Выберем r_min = 2R (R - радиус звезды), как для жестких шаров; при этом эти шары «чиркнут» друг о друга. Пусть звезды обладают параметрами Солнца: R = 0,7·10⁹ м и m = 2·10³⁰ кг, среднее расстояние между ними порядка одного светового года: l ≈ 10¹⁶ м, а средняя относительная скорость \(~\upsilon_{\infty}\) = 30 км/с. Тогда получаем

\(~ \left(\frac{b}{2R}\right)^2 = 1 + \frac{2mG}{R} \frac{1}{\upsilon^2_{\infty}} = 1 + \left(\frac{\upsilon_{II}}{\upsilon_{\infty}}\right)^2 = 425\) ,

где υ_II - вторая космическая скорость, т.е. скорость «убегания» от звезды. Эта оценка показывает, что «сечение столкновения» πb² заметно превосходит таковое для случая невзаимодействующих шаров, равное π(2R)². А для среднего времени между такими столкновениями из выражения (4) получим

\(~\tau \sim \frac{(10^{16})^3}{\pi \cdot 425(2 \cdot 0,7 \cdot 10^9)^2 \cdot 3 \cdot 10^4}\) с ≈ 10³² с ≈ 3·10²⁴ лет.

Конечно, экологи и политологи могут возразить: при «соприкосновении» звезд (когда r_min = 2R) перестанут существовать их планетные системы, а сами звезды еще до этого сильно вытянутся навстречу друг другу. Так что допустимое расстояние, с точки зрения целостности системы планет (по крайней мере, ближайших к своему светилу), по-видимому, должно превосходить орбиту Плутона, радиус которой составляет приблизительно десять тысяч радиусов Солнца, т.е. должно быть r_min ≥ 10⁴ R. Тогда сечение взаимодействия вырастет в 10⁸ раз, и во столько же раз изменится среднее «время жизни» планетных систем в нашем гипотетическом звездном газе. Все равно это время много больше времени существования известных на Земле цивилизаций.

В газовой плазме, содержащей положительные и отрицательные частицы, сила взаимодействия между парой частиц тоже обратно пропорциональна квадрату расстояния между ними, только она может быть как положительной, так и отрицательной (закон Кулона). В теории плазмы часто под сечением взаимодействия частиц понимают такое прицельное расстояние, для которого угол разворота частиц χ после «столкновения» равен 90° (см. рис.1). А что же газ молекул?

Молекулы, как уже сказано, тоже взаимодействуют не совсем как жесткие шарики. Правда, их сила взаимодействия и потенциальная энергия изменяются с расстоянием гораздо резче, чем гравитационные силы (F ~ -r^-7, E_p ~ -r^-6), поэтому они «чувствуют» друг друга только на близких расстояниях, сравнимых с их размерами. Если учесть, что средняя кинетическая энергия теплового движения молекул пропорциональна температуре, то соотношение (3) можно записать в виде

\(~ \left(\frac{b}{2 r_m}\right)^2 = 1 + \frac{\beta}{r^6_m \cdot \frac 32 kT}\) ,

где r_m - «радиус» молекулы, k — постоянная Больцмана, T - температура. Отсюда видно, что именно можно понимать под «радиусом молекулы» r_m. Действительно, для высоких температур последним слагаемым можно пренебречь, тогда b стремится к 2r_m, a сечение столкновения молекул будет 4πr²_m. В этих условиях молекулы быстро пролетают мимо друг друга, так что сила притяжения «не успевает поработать» над их сближением. Наоборот, при понижении температуры их движения становятся замедленными, сечение столкновения πb² растет, появляется возможность конденсации. Все тела во Вселенной тоже стремятся «сконденсироваться», но, слава Богу, никак не могут этого сделать благодаря начальным импульсам, прицельным расстояниям (и другим факторам).

Конечно, среднее время между столкновениями для молекул много меньше, чем для звезд. Например, в воздухе при комнатных условиях оно порядка наносекунды. Действительно, принимая радиус молекулы r_m ~ 3·10^-10 м, концентрацию n ~ 3·10²⁵ м^-3, скорость теплового движения \(~\upsilon_{\infty}\) ~ 500 м/с, по формуле (4) получим τ ~ 10^-9с. При этих столкновениях сами «планетные системы» молекул (их электронные облака) существенно участвуют в процессе взаимодействия: в отличие от звезд, здесь сила притяжения сменяется силой отталкивания.

Рис. 3

Вспомним еще, что великие физики, внесшие немалый вклад в кинетическую теорию вещества, любили лично рассчитывать траектории взаимодействующих тел. В качестве примера на рисунке 3 приведены гиперболические траектории альфа-частиц вблизи тяжелого атомного ядра, построенные самим Эрнестом Резерфордом в 1911 году. Около каждой траектории написано значение угла разворота альфа-частицы после столкновения (сравните с рисунком 1). В этом случае электрические заряды обеих частиц (альфа-частицы и ядра) имеют один знак к F ~ +r^-2.

Рис. 4

На рисунке 4 изображено несколько траекторий нейтральных молекул относительно такой же фиксированной молекулы S для случая их взаимодействия с силой, обратно пропорциональной пятой степени расстояния (F ~ +r^-5). Эти молекулы «изобрел» сам Джеймс Клерк Максвелл (они так и называются «максвелловскими молекулами»), и он же сделал этот рисунок еще в прошлом веке.

Хотя в приведенных примерах взаимодействующие частицы считались точками, из рисунков ясно видно, что при «столкновении» они как бы натыкаются на невидимую преграду отнюдь ненулевых размеров. А ведь все эти молекулы, ядра, альфа-частицы, в отличие от звезд, трудно разглядеть. Как тут не восхититься человеческим разумом1 Что и сделал еще один замечательный физик и философ: «Все тела, небесный свод, звезды, Земля и ее царства не идут в сравнение с самым низким из умов, ибо ум несет в себе знание обо всем этом, тела же не знают ничего» (Блез Паскаль).