Kvant. Фокус шара

Викторов Д. Фокус шара // Квант. — 2006.— № 5. — С. 30-31.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

И даль свободного романа

Я сквозь магический кристалл

Еще не ясно различал.

А.С. Пушкин

Однажды у меня в руках оказался оптический раритет — хрустальный шар диаметром 5,5 сантиметров, изготовленный предположительно в Великобритании. Предпоследний владелец использовал этот магический кристалл в конце XIX — начале XX века (точный год изготовления изделия неизвестен). Сквозь толщу лет пробиваются староанглийские слова, переведенные на русский язык:

«...Наблюдатель должен сесть спиной к свету, держа шар на ладони руки, которая может удобно покоиться на коленях, или шар можно поместить на столе на подставке под ним и поставить сзади экран из черного бархата или темного материала. Последний физически помогает отключить боковой свет и отражение.

Постоянное «глядение» в полной тишине абсолютно необходимо, так как в отличие от других оккультных явлений отвлечение внимания или первичного (обычного) сознания очень неблагоприятно.

Успех обнаруживается, когда сфера, прекращая отражать, становится молочной. Появляется туманный цвет (обычно красный и его дополнительный — зеленый), превращаясь в темноту, которая откатывается прочь, подобно занавесу, который открывает взгляду наблюдателя картины, сцены, фигуры в движении, интересные сентенции и т.д.

Оживление скрытой памяти или воспоминаний о будущем является одной из главных особенностей этого опыта».

Признаюсь, что у меня не получилось разглядеть в шаре что-либо необычное. Видимо, я отношусь к тем 25% людей, которые «ничего не смогут сделать вообще», как говорится в обращении к читателю (покупателю шара). Из этого,конечно, не следует, что ни у кого не получится, хотя инструкция, с современной точки зрения, и выглядит весьма фантастично. С другой стороны, магические кристаллы выпускались в XIX веке явно не единичными экземплярами. И если бы в них ничего и никому нельзя было увидеть, то кто бы их стал приобретать? В любом случае, последнее слово за достаточно массовым экспериментом...

В солнечную погоду легко экспериментально убедиться в том, что шар фокусирует солнечные лучи, действуя как собирающая линза. Данный шар собирает лучи на расстоянии 5 мм от его поверхности.

Интересно, что маленькие капельки воды на листьях растений имеют почти сферическую форму (из-за значительного преобладания сил поверхностного натяжения над силой тяжести). Такие капельки, фокусируя солнечные лучи на листьях, точечно обжигают их. Вот почему растения не надо поливать в то время, когда они освещены солнцем.

Рис. 1

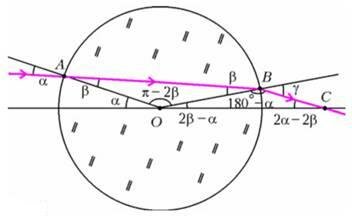
Рассчитаем теперь теоретически фокусное расстояние шара F = OC (рис.1). Рассмотрим луч, идущий вблизи одной из главных оптических осей шара параллельно ей. Место пересечения вышедшего из шара луча и оси — точка С — и есть фокус «толстой» линзы, т.е. нашего шара. Параксиальность лучей гарантирует нам, что углы α, β, γ будут малыми, т.е. значительно меньшими одного радиана. По закону преломления света в точках А и В имеем соответственно

\(~\begin{matrix} \sin \alpha = n \sin \beta \\ n \sin \beta = \sin \gamma \end{matrix}\) ,

где n — показатель преломления материала шара. Отсюда получаем γ = α. Применим к треугольнику ОВС теорему синусов:

\(~\frac{F}{\sin (180^{\circ} - \alpha)} = \frac{R}{\sin (2 \alpha - 2 \beta)}\) ,

откуда получим

\(~F = \frac{R \sin \alpha}{\sin (2 \alpha - 2 \beta)}\) ,

где R — радиус шара. Так как синус малого (в радианной мере) угла можно (и нужно) заменить самим углом, то окончательно имеем

\(~F = \frac{R \alpha}{2(\alpha - \beta)} = \frac{Rn}{2(n - 1)}\) . (1)

Факт отсутствия здесь величины β говорит о том, что все параксиальные лучи собираются в одной точке С, т.е. мы нашли действительно фокус.

Полученная формула дает возможность, используя предыдущие измерения, узнать показатель преломления стекла, из которого изготовлен шар:

\(~n = \frac{2F}{2F - R} = \frac{4F}{4F - d} = \frac{4 \cdot 3,25}{4 \cdot 3,25 - 5,5} = 1,73\) .

Видим, что магический кристалл сделан из качественного оптически плотного стекла.

Из формулы (1) для фокусного расстояния легко вывести, что

при 1 < n < 2 F > R, при n = 2 F = R, при n > 2 F < R.

Ясно, что рисунок 1 и выведенная на его основе формула справедливы при 1 < n < 2. А для n > 2 придется сделать другой рисунок (рис.2) и получить другую формулу фокуса шара.

Рис. 2

Вычисления весьма похожи на первый случай, поэтому будем кратки: применим теорему синусов к треугольнику АОС и запишем закон преломления света в точке А. Синусы малых углов сразу заменим самими углами. Тогда из уравнений

\(~\frac{F}{\beta} = \frac{R}{\alpha - \beta}\) и \(~\alpha = n \beta\)

сразу находим

\(~F = \frac{R}{n - 1}\) . (2)

Отметим, что для n = 2 подходят обе формулы фокусного расстояния шара — (1) и (2). А бывает ли показатель преломления стекла больше двух? Обычно в задачах встречаются числа, меньшие двух, но в «Справочнике по физике» А.С.Еноховича, например, указан диапазон показателей преломления оптического стекла от 1,47 до 2,04. Можно надеяться, что при неизбежном совершенствовании техники и технологии изготовления оптического стекла удастся получить образцы и с большими показателями преломления.

В заключение сравним «толстую» и «тонкую» линзы. Если для шара мы получили две разные формулы фокусного расстояния: одну для n ≤ 2, другую для n ≥ 2, то для тонкой линзы такая формула, как известно, одна:

\(~F = \frac{1}{(n - 1) \left( \frac{1}{R_1} + \frac{1}{R_2} \right)}\) ,

где R₁ и R₂ — радиусы сферических поверхностей, ограничивающих тонкую линзу. В частности, при R₁ = R₂ = R

\(~F = \frac{R}{2(n - 1)}\) . (3)

Видно, что формула (3) отличается и от формулы (1), и от формулы (2).