Kvant. Теорема электростатики

Кикоин А.К. Теорема, позволяющая решать основные задачи электростатики //Квант. — 1984. — № 12. — С. 18-20.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Известно, что электростатическое поле часто изображают при помощи силовых линий. Попытаемся установить связь между числом силовых линий N и зарядом q, создающим электрическое поле. Для этого введем понятие потока электрического поля.

Потоком электрического поля через некоторую поверхность будем называть произведение ES, где S — площадь поверхности, а Е — модуль вектора напряженности электрического поля, перпендикулярного этой поверхности. (Понятие «поток» здесь введено по аналогии с потоком жидкости, протекающей через поперечное сечение трубы площадью S в единицу времени, который, как известно, равен υS («Физика 8», §65).)

Рис. 1

Начнем с простейшего случая — одного точечного заряда. Картина силовых линий поля, созданного положительным точечным зарядом q, изображена на рисунке 1. Рассмотрим сферу радиуса r, центром которой служит сам заряд q, и определим поток электрического поля через поверхность этой сферы. Силовые линии, выходящие из заряда, перпендикулярны поверхности сферы, и в каждой точке сферы, модуль напряженности поля равен

\(~E = \frac{q}{4 \pi r^2 \varepsilon_0}\) , (1)

где ε₀ = 8,85·10^-12 Кл²/(Н·м²)— электрическая постоянная. Но 4πr² — это площадь поверхности сферы. Обозначив ее через S, получим:

\(~ES = \frac{q}{\varepsilon_0}\) . (2)

Отсюда видно, что поток через поверхность сферы электрического поля, созданного точечным зарядом, не зависит от радиуса сферы, а зависит только от самого заряда q. Поэтому, если провести ряд концентрических сфер, то поток электрического поля через все эти сферы будет одинаковым. Очевидно, что и число силовых линий, пересекающих эти сферы, тоже будет одинаковым.

Условились число силовых линий, выходящих из заряда, принимать равным потоку электрического поля:

\(~N = ES = \frac{q}{\varepsilon_0}\) . (3)

Отношение \(~\frac NS\), представляющее собой число силовых линий, пересекающих единицу площади поверхности, перпендикулярной (ортогональной) силовым линиям, называют густотой силовых линий. Ясно, что она характеризует величину напряженности поля в данном месте.

Можно показать, что поток электрического поля, а значит и число силовых линий, равняется \(~\frac{q}{\varepsilon_0}\) не только для поля одного точечного заряда, но и для поля, создаваемого любой совокупностью точечных зарядов, в частности — заряженным телом. Тогда в формуле (3) q означает алгебраическую сумму всей совокупности зарядов. Мало того, если сферу заменить любой другой замкнутой поверхностью, то поток электрического поля, а следовательно и число силовых линий, пересекающих ее, не изменится.

Утверждение, что поток электрического поля и число силовых линий через замкнутую поверхность, внутри которой находится система зарядов, равняется \(~\frac{q}{\varepsilon_0}\), где q — алгебраическая сумма зарядов, называется теоремой Гаусса.

Воспользуемся теоремой Гаусса для решения некоторых конкретных задач электростатики.

Чему равна напряженность электростатического поля внутри проводника?

Известно, что проводник — это такое тело, в котором имеются свободные заряды. Эти заряды действительно свободно могут перемещаться по всему объему проводника. Единственным препятствием для их передвижения служит поверхность проводника, которую они сами покинуть не могут.

Рассмотрим изолированный проводник, которому сообщен электрический заряд. Вокруг такого проводника, конечно, создается электростатическое поле. Докажем, что внутри заряженного проводника электростатическое поле отсутствует, то есть напряженность поля равна нулю.

Как известно, в незаряженном проводнике отрицательный заряд всех электронов точно сбалансирован положительным зарядом всех протонов, и их суммарный заряд равен нулю. Но если проводник заряжен, то баланс зарядов нарушается. В проводнике создается избыток свободных электронов, если он заряжен отрицательно, или избыток протонов (недостаток электронов), если он заряжен положительно. В первом случае, взаимно отталкиваясь, избыточные электроны разойдутся друг от друга на максимально возможные расстояния, вследствие чего они расположатся на поверхности проводника (которую покинуть не могут). Внутри же проводника баланс зарядов восстановится, и там суммарный заряд снова станет равным нулю.

Во втором случае, наоборот, часть электронов с поверхности проводника, вследствие сил притяжения к положительным зарядам, устремится внутрь проводника и сбалансирует избыточные положительные заряды. Суммарный заряд внутри проводника снова станет равным нулю, а избыточный положительный заряд сосредоточится на его поверхности.

Выходит, что заряд любого знака, сообщенный проводнику, располагается на его поверхности. Внутри же проводника, то есть внутри замкнутой поверхности, которой в данном случае служит поверхность самого проводника, заряд ранен нулю (q = 0). Но тогда из теоремы Гаусса следует, что

\(~E = \frac{q}{\varepsilon_0 S = 0}\) ,

то есть внутри проводника поля нет.

Как направлены силовые линии у поверхности заряженного проводника?

Рис. 2

На любой свободный электрон, находящийся на поверхности заряженного проводника, действуют силы со стороны остальных зарядов поверхности (в объеме проводника сумма положительных и отрицательных зарядов равна нулю). Имея возможность свободно перемещаться по поверхности, электроны сами расположатся так, чтобы результирующая сила, действующая на каждый из них вдоль поверхности, стала равной нулю. Это означает, что проекция напряженности поля на направление касательной к поверхности проводника в любой ее точке равна нулю. А это возможно только при условии, что силовые линии поля направлены перпендикулярно поверхности заряженного проводника (рис. 2).

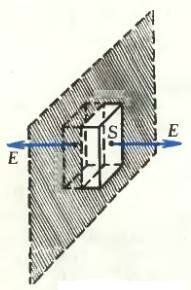
Какова напряженность поля, созданного заряженной плоскостью?

Рис. 3

На рисунке 3 изображен участок заряженной проводящей плоскости с площадью S, на который приходится заряд q.

Мы знаем, что силовые линии поля, созданного этой плоскостью, всюду перпендикулярны к ней. А чему равняется модуль напряженности электрического поля?

Окружим выбранный участок плоскости замкнутой поверхностью, через которую силовые линии проходят под прямым углом к ней. Для плоскости такой поверхностью служит, например, прямоугольный параллелепипед с основаниями, параллельными плоскости. Силовые линии поля перпендикулярны только этим основаниям, остальные четыре грани параллелепипеда параллельны силовым линиям. Площадь обоих оснований равна 2S.

Из теоремы Гаусса следует, что

\(~E cdot 2 S = \frac{q}{\varepsilon_0 S = 0}\) , откуда \(~E = \frac{q}{2 \varepsilon_0 S = 0}\) .

Эта формула приведена в §45 «Физики 9» без вывода. Из формулы видно, что напряженность поля в любой его точке не зависит от расстояния до заряженной плоскости. Такое поле называют однородным.

Чему равна напряженность поля заряженного проводящего шара?

Рис. 4

Поскольку шар проводящий, силовые линии поля всюду направлены перпендикулярно его поверхности, то есть по радиусам (рис. 4). Найдем модуль напряженности поля в любой точке М, находящейся на расстоянии R от центра шара. Проведем через эту точку замкнутую поверхность, ортогональную силовым линиям поля. Такой поверхностью служит сфера радиуса R и площадью 4πR², концентрическая поверхности проводящего шара.

По теореме Гаусса \(~ES = \frac{q}{\varepsilon_0}\). Отсюда

\(~E = \frac{q}{\varepsilon_0 S} = \frac{q}{4 \pi R^2 \varepsilon_0}\)

— заряженный шар создает вокруг себя такое же поле, как точечный заряд, помещенный в центре шара (см. рис. 4).