Kvant. Тема с вариациями

Эпштейн В. Тема с вариациями //Квант. — 2008. — № 1. — С. 34-35.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Структура курса физики иногда напоминает музыкальные формы. Простые темы (народные мотивы) композитор разворачивает вариациями, и в результате получается, к примеру, оркестровая симфония. Простые школьные задачи (поучительные сами по себе) демонстрируют идеи, лежащие в основе фундаментальных физических теорий. Вот пример такого рода.

Тема — задача 35

(«Сборник задач по физике» А. П. Рымкевича, 1992 г.)

Расстояние s необходимо проехать на лодке туда и обратно один раз по реке, скорость течения которой υ_R, а другой раз по озеру. Скорость лодки относительно воды оба раза υ_L. Докажите, что поездка туда и обратно по реке всегда занимает больше времени, чем по озеру.

Предварительный анализ

Первая (и вполне естественная) реакция на условие задачи — времена равны: выигрыш времени при движении по течению компенсируется потерей времени на обратном пути. Более глубокий анализ (или, для физиономистов, выражение лица преподавателя) показывает, что все не так просто. Компенсация, конечно, имеется, но не полная. К этому выводу можно прийти, исходя из качественных соображений, которые стоит запомнить: их можно будет применить при решении других задач.

Рис. 1

1) Придадим параметрам задачи допустимые значения, при которых ответ становится очевидным.

В нашем случае при υ_R > υ_L катер, движущийся по реке, никогда не вернется в исходный пункт (рис. 1). Можно предположить, что и при других значениях скоростей время движения в реке будет больше, чем в озере.

2) Сравним времена воздействия различных факторов.

В нашей задаче время движения против течения заведомо больше, чем по течению. Таким образом, фактор, мешающий движению, действует дольше, чем фактор помогающий. Следует, очевидно, ожидать, что мешающий фактор будет превалировать над помогающим.

Решение задачи

Время движения в озере равно

\(~t_1 = \frac{2s}{\upsilon_L}\) .

Время движения в реке составляет

\(~t_2 = \frac{s}{\upsilon_L + \upsilon_R} + \frac{s}{\upsilon_L - \upsilon_R} = \frac{2\upsilon_L s}{\upsilon^2_L - \upsilon^2_R} = \frac{2s}{\upsilon_L - \frac{\upsilon^2_R}{\upsilon_L}}\) .

Видно, что время движения в реке больше, так как числители обеих формул одинаковы, в то время как знаменатель второй заведомо меньше знаменателя первой.

Вариации на тему задачи 35

Рис. 2

Рассмотрим конструкцию прибора для определения скорости движения лодки относительно воды. Прибор представляет собой жесткое основание, на котором располагаются источник звука и отражатель (рис. 2). Для измерений прибор закрепляют на корпусе лодки снаружи так, чтобы во время движения прибор не увлекал воду.

Измеряется время, за которое звуковой импульс распространяется от источника до отражателя и возвращается к источнику. По этому времени легко вычисляется скорость движения лодки относительно воды. При этом необходимо учитывать следующее обстоятельство. Дело в том, что распространение звука имеет важную особенность: скорость звука относительно среды, в которой он распространяется, не зависит от скорости источника звука. (Этим распространение звука существенно отличается, например, от движения осколков разорвавшейся гранаты: если в момент взрыва граната двигалась, скорость осколков относительно гранаты суммируется со скоростью гранаты.) С учетом этого обстоятельства в системе отсчета, связанной с прибором, скорость звука будет равна υ_zv — υ_L (υ_zv — скорость звука относительно воды), когда звук распространяется от источника к отражателю, и υ_zv + υ_L при распространении в обратном направлении. Но тогда совершенно ясно, что время между излучением и приемом звукового импульса определяется формулой для времени движения лодки в реке с заменой υ_L на υ_zv и υ_R на υ_L:

\(~t_2 = \frac{2s}{\upsilon_{zv} - \frac{\upsilon^2_L}{\upsilon_{zv}}}\) .

Зная расстояние s между источником звука и отражателем и определив время t₂, мы легко определяем искомое значение скорости лодки:

\(~\upsilon_L = \sqrt{\upsilon_{zv}\left( \upsilon_{zv} - \frac{2s}{t_2} \right)}\) .

Усложним задачу. Попробуем определить скорость лодки, если величина s не известна (или изменяется). Решение можно получить, если произвести измерение времени до того, как лодка начала двигаться. Это время определяется формулой для времени движения лодки в озере с соответствующей заменой:

\(~t_1 = \frac{2s}{\upsilon_{zv}}\) .

Из двух последних формул можно исключить s и, таким образом, решить поставленную задачу:

\(~\upsilon_L = \upsilon_{zv} \sqrt{1 - \frac{t_1}{t_2}}\) .

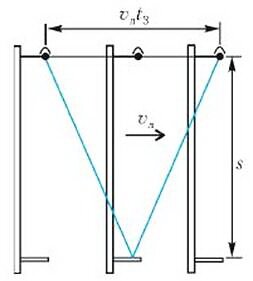
А можно ли найти скорость лодки, если измерения в условиях неподвижной лодки не проведены? Предположим также, что опустить прибор, скажем, в движущуюся вместе с лодкой ванну и определить тоже нельзя. (Например, если вода протекает сквозь лодку и ванну, как сквозь решето, — странная конструкция, не правда ли?) Оказывается, и такую задачу можно решить. Для этого необходимо развернуть прибор перпендикулярно движению лодки и произвести второе измерение времени распространения звука. Ясно, что принятый звуковой импульс распространялся вдоль равных сторон треугольника, как это показано на рисунке 3.

Рис. 3

Легко рассчитать время распространения t₃. Как видно из рисунка,

\(~\left( \upsilon_L \frac{t_3}{2} \right)^2 + s^2 = \left( \upsilon_{zv} \frac{t_3}{2} \right)^2\) ,

откуда получаем

\(~t_3 = \frac{2s}{\sqrt{\upsilon^2_{zv} - \upsilon^2_L}}\) .

Сравнивая времена t₂ и t₃, находим

\(~\frac{t_2}{t_3} = \frac{\upsilon_{zv}}{\sqrt{\upsilon^2_{zv} - \upsilon^2_L}}\) .

Отсюда и определяется скорость лодки:

\(~\upsilon_L = \upsilon_{zv} \sqrt{1 - \frac{t_3}{t_2}}\) .

«Индикатором» движения, таким образом, является отношение времен t₂ и t₃.

Вряд ли рассмотренный прибор может быть действительно использован для определения скорости корабля или самолета. Существуют более простые и надежные средства для решения той же задачи. И тем не менее, идея устройства оказывается плодотворной. Она имеет прямое отношение к революционному преобразованию классической физики — созданию теории относительности. Впрочем, речь при этом пойдет о необычной лодке, плывущей по необычному озеру.

Теория Максвелла. Плавание Земли в эфире

Во второй половине XIX века в истории науки произошло знаменательное событие. В результате создания Максвеллом теории электромагнетизма была теоретически предсказана возможность излучения электромагнитных волн, при этом были указаны их свойства и условия излучения. Также было показано, что частным случаем излучения является видимый свет. Расчеты Максвелла были подтверждены опытами Герца. В частности, выяснилось, что, в полном соответствии с общими свойствами волновых процессов, скорость распространения электромагнитной волны (света) не зависит от скорости движения источника излучения относительно среды. С другой стороны, и расчеты и эксперименты показали, что свет может распространяться в вакууме. Исходя из этого, Максвелл приходит к заключению (единственно возможному, с его точки зрения): то, что мы считаем пустотой, на самом деле упругая среда. Максвелл называет ее эфиром. Эфир заполняет всю Вселенную. Он играет для света ту же роль, что и вода для звука: звук — распространение колебаний воды, а свет — эфира.

Но почему же мы не замечаем присутствия этой среды? Ответ прост: частицы, из которых состоит эфир, настолько малы, что они свободно проходят сквозь любое тело, а следовательно, и сквозь датчик измерительного прибора. А как же тогда установить факт существования эфира? Максвелл предлагает идею, суть которой рассматривалась нами в решении задачи 35 и в вариациях на тему этой задачи. Источник звука заменяется источником света, а в качестве лодки используется наша планета Земля, которая несется по своей орбите вокруг Солнца, т.е. сквозь эфир, со скоростью 30 км/с.

Идея этого опыта была реализована Майкельсоном и Морли в 1887 году. Увы, результат эксперимента оказался отрицательным — движение Земли относительно эфира обнаружено не было (t₃ = t₂). Именно отрицательный результат опыта Майкельсона и Морли был одной из основных предпосылок для пересмотра основ классической механики и значительно способствовал признанию специальной теории относительности.

Впрочем, это уже совсем другая история.