Kvant. Таинственный остров
Стасенко А.Л. Как попасть на Таинственный остров //Квант. — 2004. — № 1. — С. 25-27.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Драматические события развернулись «Над пустынной ширью Тихого океана... 23 марта 1865 года.
...Пассажиры воздушного шара вновь заметили, что они медленно, но непрерывно спускаются... Аэронавты оказались в ужасном положении.
...Выбросив из гондолы все, что там находилось, воздухоплавателям удалось продержаться в воздухе несколько лишних часов.
...К двум часам дня аэростат оказался уже на расстоянии четырехсот футов от поверхности океана.
...Цепляйтесь все за сетку. А гондолу в воду!
...И лишь только гондола оторвалась, аэростат поднялся на высоту в две тысячи футов.
...Но, продержавшись одно мгновение вверху, аэростат опять стал спускаться. Газ утекал сквозь дыру в оболочке, и повреждение невозможно было исправить.
...Надежда была только на чудо. В четыре часа дня шар оказался всего лишь на высоте пятьсот футов от поверхности океана.
— Земля! Земля! -
Но земля находилась на расстоянии тридцати миль. Достигнуть ее аэростат мог по меньшей мере через час, да и то при условии, что ветер не переменится.
...Однако... стало совершенно очевидно, что шар больше держаться в воздухе не может. Он летел, касаясь поверхности воды.
Полчаса спустя до берега оставалось не больше мили. ...Оболочку выгнуло горбом, и ветер, надув ее, помчал по воде, словно парусную лодку.
...Он был уже в двух кабельтовых от берега, как вдруг у четырех путников вырвался крик ужаса. Взметнулся грозный вал, и шар, как будто уже лишившийся подъемной силы, неожиданно взлетел вверх. Словно избавившись от какой-то части своего груза < Смита и его собаки Топа >, он поднялся на тысячу пятьсот футов.
...В гондоле аэростата было пятеро путников и собака, но на берег выбросило только четырех человек.
Шар, освободившись от отягчающего бремени,.. взмыл вверх и исчез в небесном просторе».
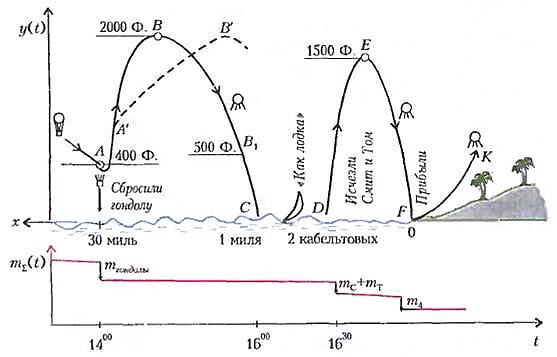
Узнали? Правильно, это «Таинственный остров» Жюля Верна. Мы подробно выписали эту последовательность событий, чтобы представить зависимость от времени массы и высоты полета в виде рисунка 1. Конечно, это только качественный рисунок, сделанный на основании показаний Ж. Верна: тогда еще не было «черных ящиков» с точной записью параметров. Но и этих сведений достаточно, чтобы попытаться сделать некоторые количественные оценки.
Прежде всего, «очевидец» трижды описывает взлет шара вверх после освобождения от очередной порции груза как быстрый процесс: «лишь только...» {АВ); «неожиданно взлетел» (DE); «взмыл вверх» (FK). Эти участки траектории отмечены на рисунке крутыми подъемами. А спуск аэростата, следующий за каждым его подъемом, происходил достаточно медленно. Таким образом, тут указаны два сильно отличающихся масштаба времени: τ↑ << τ↓. Аналогичная ситуация встречается при исследовании многих проблем физики и математики; при этом появляется плодотворная возможность провести так называемое расслоение по физическим процессам. Это означает, что в масштабе «малого времени» можно не рассматривать процессы, которые существенны на «большом времени», и наоборот. В результате исследование упрощается. Например, в нашем случае на участке быстрого подъема АВ, согласно описанию Ж.Верна, можно не учитывать изменение массы шара из-за утечки газа, а на участке спуска ВС она будет играть определяющую роль.
Но пора сделать и численные оценки, ибо, как говорит древнерусская пословица, физика без оценок - что щи без соли.
Автор сообщил нам, что «объем шара равнялся пятидесяти тысячам кубических футов». Конечно, имеется в виду начальный объем, когда аэростат еще можно было назвать шаром. Стало быть,
Отсюда легко найти радиус этого шара:
Далее, более или менее определенная информация начинается с точки A - после сброса гондолы. При этом в пределах указанных значений высоты (наибольшая высота равна 2000 Ф. ≈ 600 м) можно пренебречь изменением плотности атмосферы и считать ее равной ρ = 1,225 кг/м3.
А что это за газ, которым был наполнен шар? Конечно, это не мог быть гелий - его открыли тремя годами позднее, да и то в короне Солнца, а на Земле получили (в малых количествах) лишь через тридцать лет после описанной Жюлем Верном драмы. Может, это был теплый воздух, как у современных аэростатов? Но у этих невольных аэронавтов не было ни горелки, ни топлива. Значит, водород? Ну конечно, водород - уже лет семьдесят назад его научились добывать в промышленных масштабах, а использовать для наполнения аэростатов предложил сам Шарль, известный теперь каждому здравомыслящему школьнику. Вспомним, что молекулярные массы водорода и воздуха относятся как 2 : 29. При указанном объеме масса газа (водорода) в шаре равна
а подъемная сила (сила Архимеда) шара составляет
что соответствует возможной поднимаемой массе чуть больше полутора тонн.
А что известно о пассажирах аэростата? Сайрес Смит - «сухопарый, подтянутый»; Гедеон Спилет - «высокого роста и еще не стар - лет сорока не больше,.. энергичный, подвижный»; негр Нат - «сильный, проворный, ловкий»; моряк Пенкроф - «рослый, крепкий»; юный Герберт Браун - «смелый мальчик»; Топ - «вышколенная англо-нормандская гончая». Судя по этому описанию, пассажиры не были рыхлыми толстяками, поэтому разумно принять массу четырех счастливцев, выброшенных на берег, равной m4 = 300 кг, а массу двух упавших в океан (Смита и Топа) считать равной mC + mT = 100 кг (для круглого счета).
Итак, пока что мы насчитали суммарную массу порядка полутонны:
В начальный момент шар мог поднять массу порядка одной тонны, в которую, конечно, входит масса оболочки шара mo (неизбежная, хотя и нежелательная) и масса какого-то еще полезного груза (помимо уже учтенной массы путешественников). Мы уже никогда не узнаем общую начальную массу запаса патронов, оружия, провианта и десяти тысяч золотых франков («тяжелый мешок»), выброшенных еще до точки A (см. рис.1). Но известно, что, как только сбросили весь груз и гондолу, шар поднялся до высоты 2000 Ф. (точка В). В этой точке реализовалось равенство силы Архимеда и силы тяжести всех пассажиров, оболочки шара и водорода (газа):
Приблизительно через два с половиной часа (в точке Е) аналогичное равенство (но уже без Смита и Топа) дает
В последних двух равенствах учтено, что изменились объем шара V и масса оставшегося газа mg. Строго говоря, в точках В и E обращается в ноль вертикальная составляющая скорости, а не ускорения, или равнодействующей всех сил. Но начиная с этих точек происходит уже очень медленный спуск, при котором все силы почти уравновешены на «большом времени».
Но что же происходило на «малом времени», когда аэростат «взмывал» вверх после очередного сброса массы? Запишем изменение его кинетической энергии под действием подъемной силы, силы тяжести и силы сопротивления воздуха при изменении высоты на Δy :
Здесь m — суммарная масса путешественников, оболочки шара и газа внутри шара. А m’ — это очень важная величина, которую никак нельзя забывать при ускоренных движениях аэростатов, дирижаблей, парашютов и пузырьков газа в жидкостях. Она называется присоединенной массой. Ее возникновение можно пояснить при помощи рисунка 2. Если шар переместится в воздухе на Δy, то воздух должен заполнить пустоту позади него (что условно показано стрелками). Таким образом, ускоренное движение шара вызовет, в принципе, и ускоренное движение всей окружающей атмосферы — к шару как бы «прилипает» некоторая присоединенная масса m’. В теоретической гидромеханике показано, что она равна половине массы объема воздуха, вытесненного шаром:
Видно, что она больше суммы масс водорода в шаре и всех пассажиров.
Два первых слагаемых в скобках в правой части уравнения, описывающего изменение кинетической энергии аэростата, не требуют пояснений. Последнее слагаемое - это сила аэродинамического сопротивления. Как видно, она пропорциональна плотности воздуха, площади поперечного сечения движущегося тела и квадрату его скорости. А безразмерный множитель - это коэффициент сопротивления, в нашем уравнении выписано его значение для шара.
Конечно, в процессе подъема аэростата изменяется и масса водорода mg (за счет вытекания через отверстие), и объем V, и площадь поперечного сечения S, но мы ведь договорились о расслоении по физическим процессам: на «малом времени» эти величины можно считать неизменными.
Теперь введем обозначения:
и
и перепишем уравнение изменения кинетической энергии аэростата:
Тогда решение этого уравнения примет вид
где y0 - начальная высота, υ0 - скорость опускания до сброса гондолы (в точке А) или до «потери» Смита с Топом (в точке D), а y* и υ* - постоянные величины, смысл которых ясен из рисунка 3: как говорят физики умными словами, скорость асимптотически стремится к постоянному значению υ* на характерном расстоянии y*.
Выходит, что в наших предположениях аэростат должен вечно подниматься вверх с постоянной скоростью υ*? (Кстати, ее легко найти из нашего исходного уравнения, не решая его, а просто приравняв левую часть нулю, что и будет означать установившийся режим.) И тут пора вспомнить о медленном опускании на «большом времени». Мы не знаем, как быстро вытекал водород через отверстие в оболочке шара. Но мы можем оценить среднюю скорость опускания на участке BB1: согласно рисунку 1, в течение приблизительно двух часов шар снизился на 1500 Ф. = 500 м; значит, средняя скорость опускания была
Заметим, что при такой скорости сила сопротивления воздуха пренебрежимо мала.
Обсудим подробнее характерное расстояние, или длину релаксации
Ясно, что полная масса аэростата m должна быть не больше, чем масса воздуха в объеме шара. Поэтому
Отсюда
Таким образом, установление скорости происходит на расстоянии, равном приблизительно двум диаметрам шара, т.е. «взмывание» заканчивается на полусотне метров (~150 футов). Получается, что траектория движения аэростата выглядит скорее как АА’В’, а сила сопротивления воздуха уравновешивает убывающую подъемную силу. Конечно, к этому моменту аэростат перестал быть шаром. Если при этом вообразить его, например, цилиндром длиной πr0 (его меридиан считаем нерастяжимым), то объем его будет равен V = πr0S .
Собирая всю накопленную информацию, желающий да проведет «разбор полета»: рассчитает, как изменялись его параметры вдоль всей траектории аэростата от А до F. Но при этом надо помнить, что, во-первых, решение обратных задач (восстановления событий по их следам) - дело непростое даже при объективных данных, а во-вторых, сама объективность показаний Жюля Верна может вызывать сомнения: не летел же он рядом с аэронавтами на вертолете (иначе сам бы и помог, как благородный человек). Поэтому, например, его показания о быстром взлете и медленном спуске шара (τ↑ << τ↓) могут оказаться неправдоподобными, так что вдруг на самом деле эти времена одного порядка (τ↑ ~ τ↓). Мы же ограничимся предоставленной возможностью поговорить о физике на основе этой забавной выдумки инженера и талантливого писателя теперь уже позапрошлого века.
Приложение для желающих вычислять
1) Плотность стандартной атмосферы на разных высотах:
| y, км |
|
|
|
|
|---|---|---|---|---|
| ρ, кг/м3 |
|
|
|
|
2) 1 морская миля = 1852 м;
3) 1 кабельтов = 183 м;
4) 1 фут = 1Ф. = 0,305 м.