Kvant. Сопротивление
Маринчук М. Об электрическом сопротивлении проводников //Квант. — 1990. — № 5. — С. 53-55.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Как вам, безусловно, известно, электрическое сопротивление проводника зависит от материала, из которого он изготовлен, от размеров и формы проводника. Так, например, для однородного проводника постоянного сечения S и длиной l сопротивление
где ρ — удельное электрическое сопротивление. Иногда бывает удобнее говорить не о сопротивлении проводника, а об обратной ему величине — электрической проводимости.
Первым физиком, попытавшимся выяснить количественные закономерности прохождения постоянного электрического тока через проводники, был скромный школьный учитель из Кельна Георг Симон Ом (1789—1854). Результаты своих первых опытов Ом опубликовал в 1826 году.
Разумеется, в распоряжении Ома не было современных нам высокоточных электроизмерительных приборов и надежных источников тока, поэтому Ому по ходу дела пришлось решить целый ряд сложных практических задач.
Так, в качестве источников тока в своих первых опытах Ом использовал вольтовы столбы — чередующиеся слои двух разнородных металлов (например, серебра и цинка), разделенных бумагой, пропитанной раствором соли. При этом он заметил, что сила тока в гальванической цепи со временем заметно убывает. Ясно, что в таких условиях было почти бессмысленно заниматься установлением каких-либо количественных закономерностей. Когда же Ом познакомился с работами Зеебека (Томас Иоганн Зеебек (1770—1831) — немецкий физик), открывшего в 1821 году термоэлектрический эффект, то стал использовать в своих опытах термоэлемент, дающий достаточно стабильный ток. В установке Ома, схема которой изображена на рисунке 1, использовался термоэлемент, состоящий из висмутого стержня, спаянного с двумя медными проводами. Спай 1 поддерживался при температуре таяния льда, а спай 2 — при температуре кипения воды. Свободные концы 3 и 4 проводов были погружены в чашечки со ртутью. Сюда же погружались и предварительно зачищенные для лучшего контакта концы исследуемых проволок 5.
Узнав об опытах Эрстеда (Ханс Кристиан Эрстед (1777—1851) — датский физик), обнаружившего в 1820 году действие электрического тока на магнитную стрелку, Ом решил характеризовать силу тока величиной угла отклонения магнитной стрелки, находящейся около проводника с током. Для этого проводник помещался в плоскости магнитного меридиана (см. рис. 1), в отсутствие тока в проводнике магнитная стрелка 6 располагалась над ним и была параллельной ему, а слегка сплющенная проволока 7, к которой подвешивалась стрелка, деформирована не была. При протекании тока через проводник магнитная стрелка выходила из плоскости магнитного меридиана и закручивала подвес. Ом поворачивал головку 8, где был закреплен верхний конец подвеса, так, чтобы стрелка снова оказывалась параллельной проводнику с током, и измерял угол поворота. Этот угол и принимался в качестве характеристики магнитного действия электрического тока.
Для исследования проводимости различных металлов Ом брал проволоки одинакового поперечного сечения, но изготовленные из различных материалов, и поочередно включал их в цепь. В качестве эталона он выбрал медную проволоку определенной длины, приняв ее проводимость за 1000 условных единиц, и измерил угол поворота головки, при котором магнитная стрелка становилась параллельной проводнику с током. Затем включал в цепь проволоки из других металлов и укорачивал их до тех пор, пока угол поворота головки не становился таким же, как и в случае эталонной проволоки. По полученной при этом длине можно было судить о проводимости соответствующего материала. Таким образом Ом нашел, что проводимость золота составляет 574 условных единицы, серебра — 356, цинка — 333 и т. д.
Затем Ом исследовал проволоки из одного и того же металла, но различной толщины, и поступал с ними так же, как при определении проводимости различных металлов. Он нашел, что сопротивления проволок из одного и того же материала одинаковы, если отношения их длин равны отношениям площадей их поперечных сечений, т. е. если отношения \(~\frac lS\) у этих проволок одинаковы. Впоследствии было установлено, что сопротивление R прямо пропорционально этому отношению\[~R \sim \frac lS\]. Вводя коэффициент пропорциональности ρ, зависящий от природы материала, можно для сопротивления проволоки записать соотношение (1). Покажем теперь, как, исходя из этого соотношения, можно получить известные вам формулы для подсчета общего сопротивления системы проводников, соединенных последовательно или параллельно.
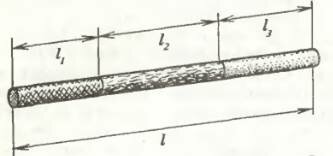
Рассмотрим проводник постоянного поперечного сечения площадью S, изготовленный из какого-либо однородного материала с удельным сопротивлением ρ. Обозначим его длину через l. Вообразим этот проводник состоящим из нескольких последовательно соединенных частей, например трех. Пусть их длины равны l1, l2 и l3 (рис. 2). Очевидно, что
Умножим обе части этого равенства на отношение \(~\frac{\rho}{S}\):
Ho \(~\rho \frac lS = R\) — сопротивление всего проводника, \(~\rho \frac{l_1}{S} = R_1\), \(~\rho \frac{l_2}{S} = R_2\) и \(~\rho \frac{l_3}{S} = R_3\) — сопротивления его первой, второй и третьей частей соответственно. Таким образом,
Это и есть искомая формула для вычисления общего сопротивления при последовательном соединении проводников.
Теперь представим тот же проводник состоящим из нескольких, например опять же трех, параллельно соединенных частей с поперечными сечениями S1, S2 и S3 (рис. 3). Аналогично предыдущему случаю,
или, после умножения на общий множитель \(~\frac{1}{\rho l}\)
В соответствии с формулой (1),
поэтому получаем
По этой формуле и можно найти общее сопротивление при параллельном соединении проводников. Формулы (2) и (3) выведены здесь лишь для частного случая конкретного вида проводников — один и тот же материал, одинаковые поперечные сечения в первом случае и одинаковые длины во втором. Однако применимы они и для самых общих случаев.