Kvant. Сверхзвуковые самолеты

Соколов Е. Сверхзвуковые самолеты и конус Маха //Квант. — 2010. — № 3. — С. 40-41

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Сверхзвуковые самолеты не только покоряют воздушные океаны, но иногда появляются и в школьных задачах. Вот - примеры.

Задача 1. Наблюдатель услышал звук сверхзвукового самолета через Δt = 10 c после того, как самолет пролетел над ним. На какой высоте летит самолет, если его скорость υ = 660 м/с, а скорость звука с = 330 м/с?

Для человека, который первый раз обращается к рассмотрению полетов сверхзвуковых самолетов, условие этой задачи в высшей степени загадочно.

-А почему так поздно наблюдатель услышал шум самолета? Ведь обычно мы слышим самолет задолго до того, как он пролетит над нами.

-Может, наблюдатель просто задумался над чем-то, поэтому и услышал звук не сразу?

-А может, и не надо ни о чем думать, а просто умножить время на скорость? Только скоростей в условии две...

Эти и другие подобные мысли роятся в голове, цепляются одна за другую и совершенно не проясняют сути дела. И это не удивительно. Привыкшим к миру дозвуковых скоростей очень сложно догадаться, чем полет сверхзвукового самолета отличается от полета обычного самолета и почему мы слышим сверхзвуковой самолет лишь после того, как он пролетит над нами. Первым эту загадку разгадал профессор Венского университета Эрнст Мах. С его именем связаны понятия «конус Маха» и «число Маха».

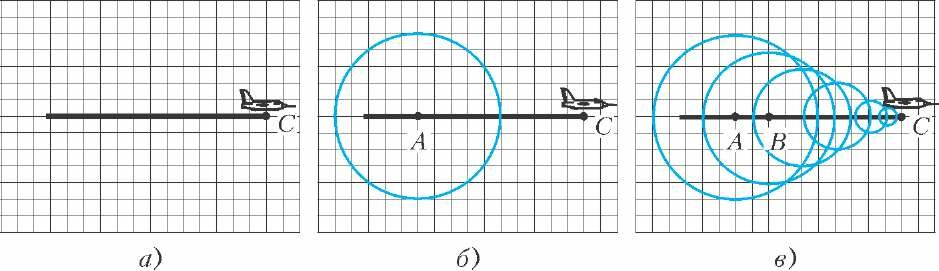
Чтобы понять, что такое конус Маха, его надо хоть раз в жизни построить самому. Сделаем это и мы. Для этого нам понадобятся лист бумаги в клетку, карандаш, линейка и циркуль. Пусть по листу нашей бумаги слева направо движется сверхзвуковой самолет, пролетающий 2 клетки в секунду, а скорость звука составляет 1 клетку в секунду. Начинаем построение. Если сейчас наш самолет находится в точке С (рис.1,а), то где он был пять секунд назад?

-На десять клеточек левее, в точке А (рис.1,б).

-Правильно. Излученный им в этот момент звук за пять секунд распространится на пять клеточек во все стороны. Поэтому ставим ножку циркуля в точку А и рисуем окружность радиусом 5 клеточек. Это мы построили геометрическое место точек, до которых дошел звук, излученный 5 секунд назад. И услышали этот звук к настоящему моменту все наблюдатели, находящиеся внутри и на самой этой окружности. Затем нарисуем круг для звука, излученного 4 секунды назад (ножку циркуля надо поставить в точку В, а радиус этого круга должен составлять 4 клеточки), потом -для трех секунд, для двух, для одной (рис.1,е). Ну а для звука, излученного только что, и рисовать ничего не надо -он еще не успел никуда распространиться, и его круг это просто точка С, сам самолет. Теперь понятно, в каких точках наблюдатели услышат звук, а в каких - нет.

Если рисовать звуковые фронты более часто, то картина станет еще подробнее, и мы увидим самое интересное -звуковые фронты-окружности имеют общие касательные (рис.2). Эти линии называют огибающими семейства окружностей. В нашей задаче эти прямые-огибающие делят все пространство на область, в которой уже был слышен звук самолета, и область, до которой звук еще не дошел. Точки самой огибающей - это точки, в которые звук только-только пришел. Вот вам и отгадка, почему сверхзвуковой самолет может уже пролететь над наблюдателем, а тот еще ничего не будет слышать - просто его еще не коснулись огибающие.

При построении на плоскости у нас для области слышимости получился, некоторый угол α . А если бы все происходило в пространстве?

- Тогда получился бы конус.

- Правильно. Этот конус и называется конусом Маха. Давайте вычислим его главную характеристику - угол раствора α . Обратимся снова к рисунку 2. В точке K звука еще нет. В точке L наблюдатель уже некоторое время слышит звук, причем в данный момент он слышит сразу и звук, пришедший к нему из точки L₁, и звук, пришедший к нему из точки L₂. А вот наблюдатель, стоящий на огибающей в точке Н, только-только услышал звук. И слышит он звук, идущий к нему из точки А, чей звуковой фронт касается огибающей в точке Н. Так как угол между касательной и радиусом, проведенным в точку касания, прямой, треугольник АСН прямоугольный. Примем, что самолет пролетел гипотенузу этого треугольника АС за время t. Тогда сама гипотенуза будет равна υt, а катет АН (это расстояние, которое прошел звук) будет равен ct, и для угла Маха получим \(~\sin \alpha = \dfrac{c}{\upsilon} \ .\) Число \(~M = \dfrac{\upsilon}{c} \ ,\) показывающее, во сколько раз скорость самолета превышает скорость звука, называют числом Маха. Используя это число, мы можем записать полученную формулу так, как когда-то ее записал сам Эрнст Мах:

\(~\sin \alpha = \dfrac{1}{M}.\)

Итак, загадки сверхзвуковых самолетов для нас больше нет. Задачи про сверхзвуковые самолеты -это задачи про движение конуса Маха. А вопросы типа «Когда наблюдатель услышит звук самолета?» следует сразу же превращать в вопросы типа «Когда конус Маха коснется точки Н?»

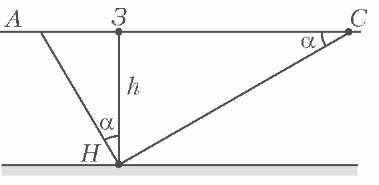
Применим эти соображения к решению задачи 1. Посмотрите на рисунок 3, на котором главный элемент - конус

Маха. Для треугольника ЗСН (зенит, самолет, наблюдатель) нам известно следующее. Угол НЗС -(по построению) прямой, угол ЗСН - это угол Маха, который для нашего самолета равен 30° , потому что Число \(~M = \dfrac{\upsilon}{c} = 2.\) И еще известна сторона ЗС: после того, как самолет был в зените, прошло время Δt, следовательно, расстояние, которое он пролетел, равно ЗС = υΔt . Теперь мы можем определить высоту полета:

\(~h = 3C tg\ \alpha = \upsilon \Delta t\dfrac{1/M}{\sqrt{1 - 1/M^2}} = \dfrac{\upsilon \Delta t}{\sqrt{M^2 - 1}} = 3810\ \)м.

Первая задача решена.

Вот вам еще несколько задач. Некоторые - для самостоятельного решения, а некоторые мы решим вместе с вами.

Задача 2. Сверхзвуковой самолет, летящий горизонтально со скоростью, вдвое большей скорости звука, пролетает мимо двух микрофонов. Через какое время после первого зафиксирует звук самолета второй микрофон, если расстояние между ними Δl = 13,2 м, а скорость звука с = 330 м/с? Рассмотрите два случая: а) микрофоны расположены горизонтально; б) микрофоны расположены вертикально.

Задача 3. Траектория сверхзвукового самолета проходит с запада на восток. Первый наблюдатель находится непосредственно под траекторией самолета, второй - на расстоянии a = 4500 м от него к югу, а третий - на расстоянии b = 8000 м к северу. Чему равны высота полета самолета и число Маха, если второй наблюдатель услышал звук на Δt₂ = 2,28 — позже первого, а третий - на Δt₃ = 3,80 — позже второго? Скорость звука с = 330 м/с.

Задача 4. Два сверхзвуковых самолета летят навстречу друг другу параллельными курсами. Число Маха для первого самолета M₁, для второго M₂. Скорость звука с. Второй летчик услышал звук первого самолета через время Δt после того, как первый летчик услышал звук второго самолета. Чему равно расстояние между траекториями самолета? Чему было равно расстояние между самолетами, когда первый летчик услышал звук? Чему было равно расстояние между самолетами, когда второй летчик услышал звук?

Задача 5. Самолет 1 летит со сверхзвуковой скоростью υ₁ . Летчик самолета 2 хочет лететь так, чтобы не слышать шума мотора первого самолета. При какой минимальной скорости ему это удастся? Какого курса ему следует при этом придерживаться?

Эту задачу давайте решать вместе.

Пусть летчик второго самолета выбрал курс, составляющий угол β с курсом первого самолета (рис.4). Его траектория - прямая, и по этой прямой движутся две точки: сам второй самолет C₂ и точка А - точка пересечения этой прямой и образующей конуса Маха первого самолета. Летчик второго самолета никогда не услышит звука первого самолета, если точка А никогда не догонит его. Поэтому скорость второго самолета должна быть больше или равна скорости точки А. Найдем эту скорость.

Рассмотрим смещение первого самолета за некоторое время Δt. В треугольнике C₁C₁'A' ' сторона C₁A' ' равна смещению Δs точки А. Используя теорему синусов, получаем

\(~\Delta s = \dfrac{\upsilon_1 \Delta t \sin \alpha}{\sin(\alpha + \beta)},\)

откуда для скорости точки А находим

\(~\upsilon_A = \dfrac{\Delta s}{\Delta t} = \dfrac{\upsilon_1 \sin \alpha}{\sin(\alpha + \beta)} = \dfrac{c}{\sin(\alpha + \beta)}.\)

Обсудим полученное выражение. Если второй самолет будет лететь в том же направлении, что и первый ( β = 0 ), то

\(~\upsilon_2 = \upsilon_A = \dfrac{c}{\sin \alpha} = \upsilon_1 .\)

- второму самолету следует иметь скорость, большую или равную скорости первого самолета. Разумный результат. Для курса, перпендикулярного курсу первого самолета ( β = 90° ), скорость точки А будет равна

\(~\upsilon_\perp = \dfrac{c}{\sin(\alpha + 90^\circ)} = \dfrac{c}{\cos \alpha} = \dfrac{c}{\sqrt{1 - 1/M^2}} = \dfrac{\upsilon_1}{\sqrt{M^2 - 1}} = 3810\ \)

А вот минимальная скорость у точки пересечения будет в том случае, когда sin (α + β) = 1, т.е. когда α + β = 90° . Это условие будет выполнено, если наша прямая будет перпендикулярна образующей конуса Маха. Тогда скорость точки пересечения будет просто равна скорости звука с. Об этой скорости часто говорят как о скорости движения волнового фронта или как о скорости движения огибающей.

Итак, ответ к нашей задаче таков. Минимальная скорость, при которой второй летчик может лететь так, чтобы ему не мешал шум первого самолета, это скорость звука с, т.е. достаточно, чтобы второй самолет был просто сверхзвуковым. А для того чтобы путешествовать в тишине, второму летчику следует выбрать курс, перпендикулярный образующей конуса Маха первого самолета.

Задача 6. Сверхзвуковые самолеты летят перпендикулярно друг другу (рис.5) со скоростями, соответствующими числам Маха M₁ = 3 и M₂ = 4 . Сколько времени второй летчик будет слышать шум мотора первого самолета, если первоначальное расстояние между самолетами L = 6600 м? Услышит ли когда-нибудь первый летчик звук второго самолета? Скорость звука с = 330 м/с.