Kvant. Радиоволны

Блиох П. Радиоволны на земле и в космосе //Квант. — 2002. — № 1. — С. 2-8.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Почему звук удается излучать равномерно во все стороны, а радиоволну нет?

Подумаем, как можно было бы сделать всенаправленный, или, как говорят, изотропный излучатель радиоволн. Очевидно, если мы хотим добиться полной симметрии излучения, нам придется сконструировать полностью симметричную антенну.

Те антенны, которые обычно используются, этому условию не удовлетворяют. Например, диполь Герца, хотя и называется симметричным вибратором, но имеет выделенное направление — ось диполя. Поэтому в объемной диаграмме направленности симметрия проявляется только в плоскости, перпендикулярной оси диполя (рис. 1). В плоскости же, проходящей через его ось, диаграмма совсем не похожа на окружность, а вдоль самой оси излучение вообще отсутствует. Что же мешает сделать полностью симметричную, т.е. сферическую антенну?

Рис. 1. Диаграмма направленности диполя Герца: а) сечение плоскостью ху; б) сечение плоскостью xz; в) объемная диаграмма

Отвлечемся ненадолго от радио и рассмотрим звуковую волну. Она представляет собой периодические изменения плотности вещества и давления в среде. Движения частиц в звуковой волне также являются периодическими, причем колебания частиц (например, молекул воздуха) происходят в том же направлении, что и распространение волны. Таким образом, в отличие от радиоволны звуковая волна является продольной. Звук, как известно, возбуждается быстро колеблющимися предметами. Если взять в качестве излучателя пульсирующую сферу, то от нее во все стороны вдоль радиусов побегут звуковые волны (рис. 2, а). На любой концентрической с излучателем сферической оболочке структура волны будет одна и та же: частицы повсюду колеблются вдоль радиуса с одинаковыми скоростями, интенсивность излучения от направления не зависит.

Рис. 2. а) Пульсирующая сфера излучает звуковые волны равномерно по всем направлениям; б) пульсирующий электрический заряд и радиальный ток не создают магнитного поля, поэтому электромагнитные волны не излучаются

Попробуем построить такой же излучатель для радиоволн. Поскольку компонентами радиоволны являются электрическое и магнитное поля \(~\vec E\) и \(~\vec B\), в качестве источников нам потребуются временные заряды и токи. Начнем с самой простой конструкции. Пусть на той же самой пульсирующей сферической оболочке, которая хорошо излучает звук, находится постоянный электрический заряд q₀, равномерно распределенный по всей поверхности. Будет ли он излучать радиоволны? Легко убедиться, что излучения не будет. Действительно, электрическое поле внутри сферы равно нулю, а вне сферы имеет только радиальную составляющую \(~E_r = \frac{q_0}{r^2}\), где r — расстояние до центра сферы. Поскольку при пульсациях оболочки r остается неизменным, то E_r = const. Что же касается магнитного поля, то его вообще нет, так как вне сферы отсутствуют токи и переменные электрические поля. Следовательно, электромагнитной волны не возникает.

Усложним нашу антенну. Пусть радиус сферы остается постоянным, а ее заряд g(t) периодически меняется. Теперь как будто бы все в порядке: вокруг пульсирующего заряда возникает радиальное переменное электрическое поле

\(~E_r = \frac{q(t)}{r^2},\)

оно породит переменное магнитное поле, и от пульсирующего заряда побежит сферически симметричная электромагнитная волна. Оказывается, этого не произойдет, так как заряд не может ни возрастать, ни убывать сам по себе. Для того чтобы изменять заряд, на сферу вдоль радиусов придется пустить переменный электрический ток. Если он равномерно распределен по всей сфере, то связь между плотностью радиального тока j_r на расстоянии r от центра и полным зарядом q(t) дается уравнением

\(~\frac{dq}{dt} = -4 \pi r^2j_r.\)

Это — так называемое уравнение непрерывности, которое связывает изменение во времени заряда в некотором объеме с током, протекающим через поверхность, ограничивающую данный объем. Уравнение непрерывности выражает фундаментальный физический закон сохранения заряда.

Чтобы понять, какое магнитное поле будет создано двумя одновременно действующими источниками — полем \(~E_r(t) = \frac{q(t)}{r^2}\) и током плотностью \(~j_r = \frac{1}{4 \pi r^2} \frac{dq}{dt}\), - надо обратиться к одному из уравнений Максвелла, а именно

\(~\operatorname{rot} \vec B = \frac 1c \left(4 \pi \vec j + \frac{\partial \vec E}{\partial t} \right).\)

Векторы \(~\vec j\) и \(~\vec E\) имеют только радиальные составляющие, причем

\(~\frac{\partial E_r}{\partial t} = \frac{1}{r^2} \frac{dq}{dt} = -4 \pi j_r.\)

Поэтому правая часть уравнения Максвелла равна нулю, и электромагнитная волна вокруг пульсирующего заряда (с учетом обязательно существующего тока) не возникает.

Собственно говоря, об этом можно было бы догадаться и без всяких расчетов, так как в сферически симметричном распределении тока нет никакого преимущественного направления, вокруг которого можно было бы нарисовать замкнутую линию индукции магнитного поля (рис. 2,б).

Итак, попытка повторить для радиоволн ту же самую конструкцию, которая обеспечивала изотропное излучение звука, оказалась неудачной. Попробуем придумать что-нибудь похитрее. Возьмем очень много маленьких дипольных излучателей и расположим их равномерно по сфере так, чтобы добиться одинакового излучения по всем направлениям. Оказывается, сделать это не удастся, как бы мы ни располагали диполи, и причина здесь кроется в поперечности электромагнитной волны.

Суть наших рассуждений можно пояснить следующим «зоологическим» примером. Представим себе ежа, свернувшегося в шар и распустившего свои иглы вдоль радиусов. Этот напуганный еж послужит нам образцом изотропного излучателя, а иглы его будут соответствовать направлениям распространения излучаемой волны. Напомним, что в случае звуковой волны скорости движения частиц тоже направлены вдоль радиусов, чем и обеспечивается сферическая симметрия продольной волны.

Когда еж успокаивается, он опускает свои иглы на поверхность шара перпендикулярно радиусам. Это расположение игл соответствует векторным составляющим \(~\vec E\) или \(~\vec B\) в поперечной электромагнитной волне (распространение волны по-прежнему происходит вдоль радиуса). Теперь подумайте, можно ли так «причесать» ежа, чтобы поверхность шара, покрытого лежащими иглами, была совершенно однородной? Легко сообразить, что сделать этого нельзя: обязательно получатся как минимум две «макушки». Следовательно, сферическая симметрия нарушится, и изотропный излучатель поперечных волн не получится.

Можно попробовать пойти совсем иным путем: вместо того чтобы придумывать специальный способ ориентации диполей (вдоль экватора, вдоль меридианов и т.д.), что всегда приводит к выделению полюсов, расположим излучатели совершенно хаотически. Пользуясь опять-таки наглядными сравнениями, представим себе, что на покрытую клеем сферу со всех сторон сыпятся маленькие иглы-диполи, которые прилипают к сфере, имея случайную ориентацию. Ясно, что у хаотически расположенных диполей нет ни экватора, ни полюсов, т.е. мы как будто бы получим, наконец, изотропный излучатель.

Но обмануть природу, конечно, не удастся. Если число диполей невелико, то на сфере в некоторых местах появляются пробелы, нарушающие симметрию. Если, наоборот, диполей так много, что в пределах любой маленькой (по сравнению с длиной волны) площадки окажется несколько случайно ориентированных диполей, то их излучения почти полностью скомпенсируют друг друга (противоположно ориентированные диполи создают противофазные поля, ослабляющие друг друга). Но если почти не будет излучать каждая маленькая площадка, то в той же мере не будет излучать и вся сферическая антенна. Мы все же пишем «почти», потому что при случайной ориентации может оказаться избыток диполей, повернутых в какую-нибудь сторону. Этот избыток окажется источником дипольного излучения, которое, как мы знаем, не является изотропным.

Таким образом, сфера, покрытая хаотически расположенными диполями, излучает с такой же диаграммой направленности, как многовибраторная антенна со случайно ориентированными излучателями. Диаграмма направленности такой антенны не является изотропной, но в каких направлениях будет наблюдаться максимальное излучение, а в каких минимальное, заранее предсказать нельзя.

Можно ли использовать атмосферу Земли как гигантскую сферическую линзу для фокусировки радиоволн?

В стандартных условиях радиолучи искривляются в тропосфере по направлению к Земле. Поэтому радиоволны от далеких космических источников, огибая Землю со всех сторон, на некотором расстоянии от планеты сходятся в одном месте. Получается, что атмосферная оболочка действует подобно гигантской собирающей линзе. Размеры этой линзы-антенны, созданной самой природой, колоссальны (ее диаметр d ≈ 12800 км), поэтому не удивительно, что в литературе время от времени появляются довольно смелые проекты ее использования.

Предлагалось, например, воспользоваться атмосферной линзой для передачи энергии на далекие космические корабли. Для этого необходимо поместить в фокус линзы мощный источник и направить поток радиоволн, как луч прожектора, на космический корабль. Благодаря огромным размерам антенны, дифракционная расходимость пучка радиоволн оказывается очень малой:

\(~\Delta \varphi_{difr} \approx \frac{\lambda}{d}\) ≈ 8·10^-9 рад ≈ 1,6·10^-3 угл.с.

Здесь и далее в численных оценках взята длина волны λ = 10 см, такие радиоволны слабо поглощаются в тропосфере и практически не испытывают влияния ионосферы.

Слабая расходимость пучка радиоволн послужила основой и для второго проекта, в котором предлагалось использовать атмосферную оболочку как приемную антенну радиотелескопа. Поместив в фокус линзы приемное устройство, можно будет, по мнению авторов, увидеть мелкие детали далеких светящихся объектов, недоступные для обычных земных средств.

Нет необходимости объяснять, сколь заманчивы оба проекта. Но осуществимы ли они? В принципе да, т.е. атмосферную оболочку действительно можно использовать и как передающую антенну, и как гигантский радиотелескоп. Однако их реальные возможности можно оценить только после того, как будут рассчитаны коэффициент усиления линзы-антенны и ее разрешающая способность. Авторы проектов таких расчетов не делали, но мы без особого труда выполним их сами.

Рис. 3. Рефракция световых лучей в тропосфере

Начнем с оценки того минимального расстояния, на котором пересекается поток параллельных лучей после преломления в тропосфере. Сначала сделаем оценку без всяких формул, учитывая, что угол рефракции лучей света вблизи горизонта равен приблизительно 30' (рис. 3). Вследствие этого эффекта, восход Солнца наступает несколько раньше, а заход — несколько позже по сравнению с тем временем, которое соответствовало бы прямым, неискривленным лучам. Полный угол преломления светового луча, обогнувшего Землю, будет в два раза больше: φ ~ 1°. В радиодиапазоне коэффициент преломления воздуха возрастает, и эти цифры надо примерно удвоить. Поэтому угол φ на рисунке 4 уже порядка 2°. Легко рассчитать расстояние до точки пересечения лучей:

\(~X_{min} \approx \frac{a}{\varphi}\) ≈ 180000 км.

Рис. 4. Фокусировка радиоволн земной атмосферой

Мы обозначили это расстояние X_min, поскольку лучи, проходящие на некоторой высоте z над земной поверхностью, преломляются слабее и пересекают ось х на расстояниях, больших X_min.

Очевидно, что в точке пересечения лучей интенсивность радиоизлучения I может во много раз превышать исходную величину I₀. Но во сколько раз? От численного значения коэффициента усиления \(~K = \frac{I}{I_0}\) зависит реальность тех заманчивых предложений, о которых говорилось выше. Точно рассчитать величину К практически невозможно, так как для этого надо было бы знать коэффициент преломления по всей толщине тропосферы во всех местах земного шара. Однако приблизительные оценки (они нас вполне устроят) делаются легко.

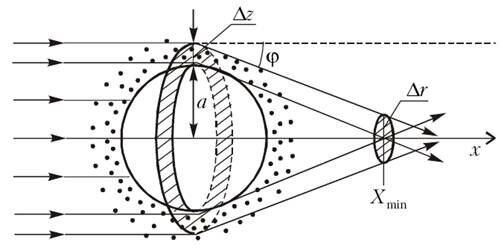
Взгляните на рисунок 4. Видно, что через круговую площадку радиусом Δr с центром на оси х в точке X_min проходят те лучи, которые прошли через узкое кольцо шириной Δz, примыкающее к земному шару. Площадь кольца (его называют входной апертурой линзы) равна приблизительно \(~S_0 = 2 \pi a \Delta z\), а площадь кружка (фокального пятна) равна \(~S = \pi (\Delta r)^2\). Из закона сохранения энергии в лучевом конусе следует, что \(~I_0S_0 = IS\), и искомый коэффициент усиления интенсивности равен

\(~K = \frac{S_0}{S} \approx \frac{2 a \Delta z}{(\Delta r)^2}.\)

Лучи, идущие на некоторой высоте r над горизонтом, не проходят через центр фокального пятна. Обозначим их удаление от оси х на расстоянии X_min через r. Между z и r существует определенная зависимость (мы установим ее несколько позже), но для небольших Δz и Δr можно считать, что

\(~\Delta z = \frac{dz}{dr} \Delta r.\)

Тогда

\(~K = \frac{2 a \frac{dz}{dr}}{\Delta r} = \frac{2 a}{\Delta r \frac{dr}{dz}}.\)

Видно, что чем меньше радиус площадки Δr, тем больше коэффициент усиления линзы.

Существует предельно малое значение Δr_min, в пределах которого могут сконцентрироваться лучи. Это ограничение связано с дифракцией волн, поэтому \(~\Delta r_{min} \approx X_{min} \Delta \varphi_{difr}\) ≈ 1,4·10^-3 км = 1,4 м. Как видим, фокальный кружок получился очень маленьким.

Рис. 5. Траектория луча, проходящего в тропосфере на высоте z над Землей

Для определения К надо еще найти производную \(~\frac{dr}{dz}\). Схема вычисления поясняется рисунком 5. Будем считать для упрощения расчетов, что тропосфера имеет толщину Н ≈ 12 км, и выше этой границы лучи не преломляются. Учитывая малость угла φ(z), связь между z и r запишем в виде

\(~r \approx (a + z) - X_{min} \varphi (r).\)

Луч, пришедший параллельно оси х, в пределах тропосферы распространяется по дуге АС. Радиус этой окружности в стандартных условиях составляет R ≈ 25000 км. Для малых φ угол преломления можно определить как отношение хорды АС к радиусу R:

\(~\varphi = \frac{AC}{R} = \frac{2 \sqrt{(a + H)^2 - (a + z)^2}}{R} \approx \frac{2 \sqrt{2a (H - z)}}{R}.\)

Интересно сравнить результаты расчета с взятым ранее значением φ ≈ 2°. При z = 0, Н = 12 км, а = 6400 км, R = 25000 км найдем φ(0) ≈ 1,7°. Получилась несколько заниженная величина, но согласие можно считать вполне удовлетворительным.

Вернемся к определению \(~\frac{dr}{dz}\). Согласно приведенному выражению для r, получим

\(~\frac{dr}{dz} \approx 1 - X_{min} \frac{d \varphi}{dz} \approx 1 + \frac{X_{min} \sqrt{2a}}{R\sqrt{H - z}}.\)

Для луча, проходящего через центр фокального пятна (r = 0, z = 0),

\(~\left. \frac{dr}{dz} \right|_{z_0} \approx 1 + \frac{X_{min}}{R}\sqrt{\frac{2a}{H}}.\)

Теперь нам известны все величины для определения коэффициента усиления, и искомая оценка K_max, соответствующая Δr_min, такова: K_max ≈ 3,7·10⁴. Получился вполне обнадеживающий результат: от атмосферной линзы можно ожидать усиления интенсивности в десятки тысяч раз. Если бы это было действительно так! Увы, наш расчет относится к идеализированной линзе, которая образуется совершенно однородной тропосферой. На самом деле коэффициент преломления воздуха меняется не только регулярным образом, уменьшаясь с высотой, что мы учли, используя радиус кривизны луча R, но и испытывает случайные отклонения от среднего значения, на что мы не обращали внимания.

Случайные изменения n(r, t) вызывают непредсказуемые отклонения луча в пределах некоторого угла рассеяния Δφ_ras. Если Δφ_ras окажется больше Δφ_difr, то радиус фокальной площадки Δr возрастет, и коэффициент усиления линзы уменьшится. С флуктуациями коэффициента преломления связано, например, мерцание далеких огней. Это красивое зрелище — настоящий бич для астрономических наблюдений. Изображения звезд «пляшут» в фокусе телескопа, ограничивая разрешающую способность инструмента. Чтобы уменьшить влияние случайных неоднородностей тропосферы, телескопы устанавливают высоко в горах, а радикальной мерой являются внеатмосферные наблюдения из космоса. Астрономы давно измерили среднеквадратическое значение Δφ_ras. Вблизи горизонта оно равно примерно 1". В диапазоне сантиметровых радиоволн эту величину надо примерно удвоить. Положив Δφ_ras ≈ 2" ≈ 10^-5 рад, найдем \(~\Delta r \approx X_{min} \Delta \varphi_{ras}\) ≈ 1,8 км и получим среднее значение коэффициента усиления \(~\mathcal{h} K \mathcal{i}\) ≈ 30. Переход от К к \(~\mathcal{h} K \mathcal{i}\) объясняется тем, что угол отклонения луча, а вместе с ним и Δr являются случайными величинами.

К сожалению, от усиления в десятки тысяч раз ничего не осталось, но и найденное значение \(~\mathcal{h} K \mathcal{i}\) все равно является завышенным. Дело в том, что наряду со сравнительно мелкомасштабными флуктуациями коэффициента преломления, которые вызывают рассеяние лучей, существуют более сильные изменения, нарушающие сферическую симметрию линзы. Воздух над океанами и над сушей, днем и ночью имеет разные метеорологические параметры, и вместе с ними меняется коэффициент преломления n(r, t). За счет этих изменений угол оптической рефракции вблизи горизонта отличается в разных местах в течение года более чем на 30". Если принять эту величину за Δφ_ras, то \(~\mathcal{h} K \mathcal{i}\) снизится до 1.

Эта цифра окончательно губит все фантастические проекты, но не устраняет саму возможность наблюдения линзового эффекта. Взгляните снова на рисунок 4. Если бы не было преломления и рассеяния лучей в атмосфере, то точка X_min находилась бы в тени Земли, и ни один луч сюда бы не попал. В оптический прибор наблюдатель увидел бы только темный диск Земли. За счет линзового эффекта и рассеяния лучей вокруг темного диска возникает светлый ореол, который при \(~\mathcal{h} K \mathcal{i}\) ~ 1 дает освещенность в точке X_min почти такую же, как и в исходном световом потоке. Для радиосвязи здесь открываются возможности передачи сигналов от одного космического корабля к другому, даже если радиолиния заэкранирована Землей, при условии, конечно, что корабли находятся достаточно далеко от Земли.

Линзовый эффект должен наблюдаться и в атмосферах других планет. В атмосфере Венеры это явление было замечено еще М.В.Ломоносовым в 1761 году во время прохождения планеты по диску Солнца. Он увидел светлый выступ вокруг темного пятна вблизи края солнечного диска и правильно объяснил его наличием у Венеры атмосферы.

Как затмения космических радиоисточников Солнцем используются для изучения солнечной короны

Из Солнца непрерывно вытекают потоки плазмы, создавая так называемый солнечный ветер. Плазма заполняет околосолнечное и межпланетное пространства. Область ее влияния охватывает огромные расстояния, значительно превосходящие радиус орбиты Земли. Плазменная корона состоит в основном из протонов и электронов. Электронная концентрация по мере удаления от Солнца спадает сначала очень быстро: от 10⁸ см^-3 до 10⁴ см^-3 на расстоянии в несколько R_c (радиус Солнца). Далее концентрация убывает намного медленнее: обратно пропорционально квадрату расстояния, и на орбите Земли составляет примерно 5-10 см^-3.

На оптическое излучение межпланетная плазма практически не влияет, но в диапазоне радиоволн, особенно на метровых и более длинных волнах, это влияние становится весьма заметным. Оно проявляется в виде регулярной рефракции и рассеяния на случайных неоднородностях короны. Наблюдая затмения Солнцем радиоисточников, извлекают много полезных сведений о распределении электронной концентрации в межпланетной среде.

Метод затменных наблюдений, или метод радиопросвечивания, был предложен независимо советским астрономом В.В.Виткевичем и английским ученым А.Хьюишем. В качестве «передатчика» чаще всего используется один из наиболее мощных источников, а именно Крабовидная туманность, или ЗС-144(название источника указывает, что он занесен под номером 144 в третий каталог Кембриджского университета). Затмения ЗС-144 происходят каждый год. Максимальная фаза приходится на 15 июня, когда Солнце проходит очень близко от Краба.

Первые наблюдения, проведенные в 1951-1953 годах, дали неожиданные результаты: было обнаружено существенное ослабление интенсивности излучения на таких больших расстояниях от Солнца, где поглощение в плазме заведомо отсутствует. Только в 1955 году удалось объяснить причину уменьшения интенсивности. Она заключается не в поглощении, а в том, что околосолнечная плазма имеет неоднородную структуру. Радиоволны рассеиваются на неоднородностях, что воспринимается как увеличение угловых размеров источника.

Далее, надо иметь в виду, что наблюдения проводились с помощью радиоинтерферометра, состоящего из далеко разнесенных друг от друга антенн. Такая система хорошо регистрирует только точечные источники, что позволяет подавить фоновые излучения Галактики и самого Солнца, которые являются в данном случае помехами. Если угловые размеры источника превышают ширину лепестковых диаграмм направленности интерферометра \(~\varphi \sim \frac{\lambda}{d}\) (где d — расстояние между антеннами), то отклик интерферометра уменьшается. Поэтому увеличение угловых размеров источника за счет рассеяния до величины \(~\sigma_{\varphi} \ge \frac{\lambda}{d}\) приводит к кажущемуся ослаблению интенсивности, хотя на самом деле она не меняется. Так была обнаружена неоднородная структура солнечной короны на очень больших расстояниях от Солнца. Раньше эти области короны были недоступны для изучения.

Конечной целью затменных экспериментов является определение плотности частиц (электронов) N в корональной плазме. Ее можно представить в виде суммы двух крмпонентов\[~N = \mathcal{h} N \mathcal{i} + \delta N\]. Первое слагаемое \(~\mathcal{h} N \mathcal{i}\) представляет собой регулярную составляющую электронной плотности. Приближенно можно считать, что величина \(~\mathcal{h} N \mathcal{i}\) зависит только от расстояния до Солнца и монотонно убывает с ростом r (сферически симметричная корона). Второе слагаемое δN - это случайная составляющая. Она, собственно, и характеризует неоднородную структуру короны. Именно с этой величиной связан угол рассеяния σ_φ, который определяется по изменениям отклика интерферометра.

Регулярная составляющая \(~\mathcal{h} N \mathcal{i}\) изучается другим способом, о котором мы сейчас расскажем. Забудем на время о наличии неоднородностей и об эффекте рассеяния. Как в этом случае будет влиять солнечная корона на распространение радиоволн? Плазменный шар с монотонно убывающей плотностью действует подобно рассеивающей линзе (коэффициент преломления плазмы n < 1). Проходя сквозь корону, радиолучи отклоняются от Солнца, и возникает так называемая радиотень (рис. 6). При движении по орбите Земля пересекает границу тени, что сопровождается сравнительно резкими изменениями интенсивности с характерным временем порядка суток. Положение границы тени для данной длины волны зависит от закона распределения \(~\mathcal{h} N(r) \mathcal{i}\). Поэтому, изучая изменения интенсивности во время затмения (в течение нескольких дней вблизи 15 июня), можно получить данные о регулярной составляющей электронной плотности в солнечной короне.

Рис. 6. Затмение Крабовидной туманности солнечной короной

В наших рассуждениях мы отвлеклись для простоты от влияния неоднородностей δN. Они существенно усложняют исследование \(~\mathcal{h} N \mathcal{i}\). Дело в том, что при измерениях с интерферометром спад интенсивности во время приближения Солнца к источнику связан одновременно с двумя факторами: переходом Земли в область тени и кажущимся увеличением углового диаметра источника за счет рассеяния.

Тем не менее, эти эффекты можно разделить, используя различную зависимость их от длины волны. Мы не будем рассказывать подробно, как это делается, но укажем на главное: наблюдения должны проводиться одновременно на нескольких волнах, желательно наиболее длинных из тех, которые проходят сквозь ионосферу, так как для них рефракция и рассеяние в солнечной короне проявляются наиболее сильно. Такой эксперимент был успешно осуществлен в июне 1965 и 1966 годов на радиотелескопе Радиоастрономического института в Харькове. Затмение источника ЗС-144 наблюдалось одновременно на четырех волнах декаметрового диапазона (7,9 м, 9,7 м, 12 м и 15 м). После обработки результатов удалось выбрать наиболее приемлемые модели распределения \(~\mathcal{h} N \mathcal{i}\) и δN.

Метод радиопросвечивания с успехом применяется и для исследования планетных атмосфер. В этом случае используются высокостабильные узкополосные передатчики, установленные на космических аппаратах. Сами же аппараты могут пролетать вдали от планеты, находиться на орбитах ее спутников или даже вести передачу с самбй поверхности планеты. Ясно, что все эти варианты расширяют возможности радиопросвечивания.

К настоящему времени достаточно детально изучены атмосферы Венеры и Марса. В частности, установлено, что они имеют ионосферы, подобные земной, но несколько меньшей плотности. Максимум электронной концентрации на дневной стороне Марса расположен на высоте примерно 140 км и равен приблизительно 1,5·10⁵ см^-3. Высота максимума на Венере та же, а сама концентрация составляет около 5,5·10⁵ см^-3.