Kvant. Пределы зоркости

Стасенко А.Л. Пределы зоркости приборов //Квант. — 2000. — № 3. — С. 39-41.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Мистер Лунд подошел к телескопу и начал смотреть на луну…

- А не видите ли вы бледных пятен, движущихся возле луны?..

- Черт возьми, сэр! Называйте меня ослом, если я не вижу этих пятен! Что это за пятна?

- Это пятна, которые видны в один только мой телескоп. Довольно! Оставьте телескоп!

…Через полчаса мистер Вильям Болваниус, Джон Лунд и шотландец Том Бекас летели уже к таинственным пятнам на восемнадцати аэростатах.

…Кто из читателей воспылает желанием ближе познакомиться с мистером Вильямом Болваниусом, тот пусть прочтет его замечательное сочинение «Существовала ли луна до потопа? Если существовала, то почему же и она не утонула?»… Между прочим, там описывается, как он прожил два года в австралийских камышах, где питался раками, тиной, яйцами крокодилов и … изобрел микроскоп, совершенно сходный с нашим обыкновенным микроскопом…» (А.Чехов. «Летающие острова»).

Действительно, среди многочисленных приборов, изобретенных физиками, широкую известность получили телескоп и микроскоп. Один из них устремлен в глубины Вселенной, другой позволяет рассматривать всякую мелочь буквально «под носом». Обсудим вкратце, как они работают.

Рис. 1

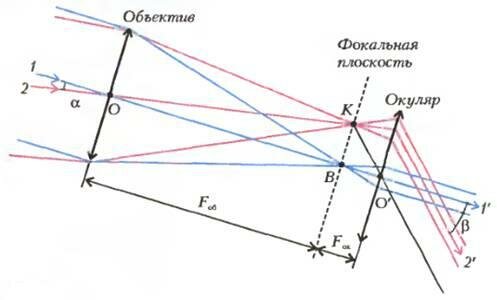
С точки зрения геометрической оптики, с телескопом все просто. Есть две соосные линзы с фокусными расстояниями F_ob у объектива и F_ok у окуляра (рис. 1). Лучи, идущие от каждой из двух рассматриваемых звезд - направления 1 и 2, — почти параллельны и, по определению фокусного расстояния, после объектива они должны собраться в двух точках В и К, лежащих в фокальной плоскости объектива. Но в телескопической системе это одновременно и фокальная плоскость окуляра, поэтому, пройдя через окуляр, лучи должны выйти гоже двумя параллельными пучками с осями 1’ и 2’. Угол между входящими лучами 1 и 2 (направлениями на две звезды) обозначим через α, а угол между выходящими лучами - через β. Легко видеть, в чем «фокус» такой телескопической системы. Из прямоугольных треугольников ОВК и О’ВК видно, что их общий катет равен

\(~BK = F_{ob} \operatorname{tg} \alpha = F_{ok} \operatorname{tg} \beta\) ,

откуда

\(~\frac{\operatorname{tg} \beta}{\operatorname{tg} \alpha} = \frac{F_{ob}}{F_{ok}} \approx \frac{\beta}{\alpha}\) (1)

(последнее приближенное равенство записано для случая малых углов, который обычно и реализуется на практике).

Полученное соотношение открывает, казалось бы, неограниченные возможности для увеличения телескопа: нужно брать как можно более длиннофокусный объектив (вот почему оптические телескопы-рефракторы такие длинные) и как можно более короткофокусный окуляр. Но тут вмешивается еще один характерный размер - длина волны λ. Как же иначе? Ведь свет - это электромагнитные волны в диапазоне 0,4 мкм ≤ λ ≤ 0,8 мкм. А любая волна, проходя около препятствия, дифрагирует. Более того, любой участок первичной волны (например, в плоскости объектива), согласно принципу Гюйгенса—Френеля, можно считать источником вторичных волн, которые затем интерферируют друг с другом всюду, где встретятся, например - в фокальной плоскости объектива.

Рис. 2

Проведем при помощи этого принципа приближенное рассмотрение дифракции света (от одной звезды) на объективе телескопа. Разобьем объектив условно на две половины (рис.2,а) и будем считать, что обе они являются источниками вторичных волн. Если принять расстояние между точками С и С’ равным половине диаметра D объектива, то разность хода волн, пришедших от них в точку М, будет приблизительно равна (см. выделенный треугольничек на рисунке 2,б)

\(~\Delta = \frac D2 \sin \theta\) .

И результат их интерференции будет определяться значением этой разности. Например, в точке В (да и на всей оптической оси OB) имеем θ = 0 и Δ = 0; значит, эти две волны будут усиливать друг друга, так что в фокусе объектива (если туда поставить пластинку, перпендикулярную оптической оси) будет светлое пятно.

Можно уточнить этот результат, считая, что точки С и С’ соответствуют центрам тяжести каждой из половин объектива. Нетрудно показать (например, сделав полукруг из картона и уравновесив его на лезвии ножа) или посмотреть в справочнике, что центр масс полукруга находится на высоте \(~y_c = \frac{4}{3 \pi} \frac D2\) над его диаметром. Значит, разность хода Δ двух сферических волн, исходящих из точек С и С’ под утлом θ к оптической оси, будет равна

\(~\Delta = 2 y_c \sin \theta = \frac{8}{3 \pi} \frac D2 \sin \theta\) . (2)

Будем теперь перемещать вверх (или вниз) точку наблюдения в фокальной плоскости. Тогда угол θ будет расти, а вместе с ним будет расти разность хода Δ. Очень важно найти, при каком значении угла θ_{1 min} эта разность хода станет равной \(~\Delta_{1\ min} = \frac{\lambda}{2}\), так что волны погасят друг друга. Из выражения (2) имеем

\(~\sin \theta_{1\ min} = \frac{3 \pi}{8} \frac{\lambda}{D} = 1,18 \frac{\lambda}{D} \approx \theta_{1\ min}\) .

Конечно, принцип Гюйгенса—Френеля предписывает складывать элементарные возмущения от малых площадок первичной волны (т.е. интегрировать). При этом нам пришлось бы иметь дело с так называемыми функциями Бесселя, которые в случае осевой симметрии являются аналогами «обычных» синусов и косинусов, характерных для одномерных задач (например, струны гитары). И тогда получился бы более точный результат:

\(~\sin \theta_{1\ min} = 1,2 \frac{\lambda}{D}\) . (3)

Видно, что наше грубое рассмотрение всего лишь на четыре процента отличается от более точного - не так уж и плохо. Но почему для нас так важен этот угол? Потому что он дает радиус первого темного кольца \(~BM = F_{ob} \cdot \theta_{1\ min}\), окружающего светлое пятнышко - изображение звезды в фокальной плоскости объектива. Получается, что это вовсе не точка, как утверждает геометрическая оптика. Значит, вторая звезда с угловым расстоянием α от оптической оси тоже даст светлое пятнышко в фокальной плоскости, и теперь все дело в том, насколько далеко оно окажется от изображения первой звезды. Великий Рэлей предложил простой критерий: должно быть

\(~\alpha \ge \theta_{1\ min}\) , (4)

иначе изображения двух звезд наложатся друг на друга уже в фокальной плоскости объектива и далее никакими ухищрениями их не разделить.

Рис. 3

Но оторвемся от звезд и заглянем в микроскоп. Обычное построение изображений предмета в объективе и окуляре (в приближении тонких линз) дано на рисунке 3. Тут существенно, чтобы предмет находился за фокусом объектива - тогда изображение 1’ будет действительным, а это изображение чтобы находилось между окуляром и его фокусом — тогда окончательное изображение 1’’ будет мнимым.

Геометрическая оптика дает для увеличения микроскопа следующее выражение (см. рис.3):

\(~\frac Xx = \frac{D_0 \delta}{F_{ok}F_{ob}}\) ,

где δ - расстояние между фокусами объектива и окуляра, D₀ - так называемое расстояние наилучшего зрения. Увеличение микроскопа может быть значительным. Например, для характерных значений F_ob = 2 мм, F_ok = 15 мм, δ = 160 мм и D₀ = 250 мм получим \(~\frac Xx = 1335\).

Казалось бы, это не предел - надо лишь делать линзы все более совершенными геометрически (шлифовать), устранять их недостатки (апланатизм, астигматизм, хроматическую и сферическую аберрации, дисторсию...) и все будет в порядке. Но и тут вмешалась все та же λ.

Рис. 4

Теорию разрешающей способности микроскопа разработал Аббе (о нем совсем недавно рассказывалось в «Кванте» - см. №1 за 2000 г.). Он предложил рассмотреть в микроскоп дифракционную решетку (рис.4). Какую минимальную информацию можно получить об этой решетке? Конечно, прежде всего можно узнать ее период d.

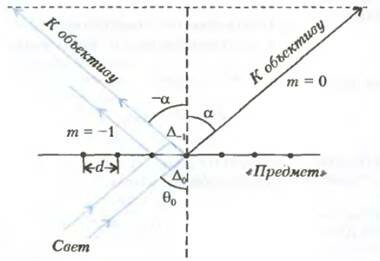
Как известно, при прохождении через решетку света с длиной волны λ должен получиться набор дифракционных максимумов. Если свет падает на решетку под углом θ₀, то направление на эти максимумы определяется условием

\(~\Delta_m - \Delta_0 = d \sin \theta_{m\ max} - d \sin \theta_0 = m \lambda\) . (5)

Чтобы микроскоп дал информацию о периоде d, в его объектив должны прийти по крайней мере два луча, соответствующих двум соседним максимумам дифракционной картины, например m = 0 к m = -1. Именно такой предельный случай α = θ₀ и -α = θ_{-1 max} изображен на рисунке 4. Заметим, что период решетки d, который мы стремимся рассмотреть, конечно, очень мал - порядка микрометров. В этом масштабе объектив микроскопа и его фокусное расстояние (порядка миллиметров) таковы, что сам объектив нужно было бы изобразить далеко за пределами рисунка (порядка метров); поэтому он показан штриховой линией лишь условно (а идущие к нему от узлов решетки лучи почти параллельны).

Итак, из условия (5) получим \(~2 d \sin \alpha = \lambda\) (α называется апертурным углом). Значит, при заданной длине волны подсветки наименьший период решетки, который можно «рассмотреть» в микроскоп, равен \(~d_{min} = \frac{\lambda}{2 \sin \alpha}\). Можно еще облегчить дело: если между решеткой и объективом поместить среду с коэффициентом преломления n (например, капнуть какую-либо жидкость) , то увеличится оптическая разность хода (ведь в этой среде скорость света и длина волны станут в n раз меньше). В результате получим

\(~d_{min} = \frac{\lambda}{2n \sin \alpha}\) . (6)

Теперь сравним разрешающие способности телескопа и микроскопа. Получается, что мы выдвигаем прямо противоположные требования:

для телескопа — \(~\frac{\lambda}{D} \approx \alpha_{min}\) желательно делать как можно меньше;

для микроскопа — \(~\frac{\lambda}{d} \approx 2n \sin \alpha\) желательно делать как можно больше.

Отсюда понятно стремление строить телескопы с возможно большим диаметром входного «зрачка», а микроскопы — с возможно меньшим фокусным расстоянием объектива (чтобы sin α был как можно ближе к единице) и при этом пространство между объективом и предметом наблюдения следует заполнить жидкостью с возможно большим показателем преломления n (так называемая иммерсионная техника).

Что же достигнуто человечеством?

Самый большой диаметр объектива оптического телескопа D ~ 6 м. Для «средней» длины волны света λ ~ 0,6 мкм из выражений (3) и (4) будем иметь α_min ~ 10^-7. Принимая радиус Вселенной R ~ 10²⁶ м, для двух разрешимых точек на ее «границе» получим

\(~l_{min} \sim R \alpha_{min} \) ~ 10¹⁹ м.

В случае микроскопа положим sin α ≤ 1, и n ≈ 1,6 (коэффициент преломления анилина). Тогда из равенства (6) найдем

\(~d_{min} \ge \frac{\lambda}{4} \) ~ 0,1 мкм = 10^-7 м.

Таковы характерные пределы возможностей этих замечательных оптических приборов.