Kvant. Осцилляторы-кентавры

Рыбин Б. Осцилляторы-кентавры //Квант. — 1995. — № 5. — С. 39.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Человек давно мечтал о создании новых живых организмов на основе имеющихся в природе. Сначала это делалось на уровне фантазии — вспомните, скажем, человека-амфибию из романа А.Р.Беляева или кентавров из мифов Древней Греции. В настоящее время проблема постепенно переходит в практическую плоскость. Например, когда речь идет о пересадке органов от одного живого организма к другому. При этом оказалось, что при соединении частей от разных, пусть даже родственных, организмов возникает проблема несовместимости, и требуется преодолеть значительные трудности, чтобы вновь созданный организм оказался жизнеспособным.

Нечто похожее можно наблюдать и в физике. Существует два основных класса колебательных систем — механические и электрические. В качестве типичного примера механического осциллятора можно рассмотреть пружинный маятник, а электрического — электрический колебательный контур.

Рис. 1

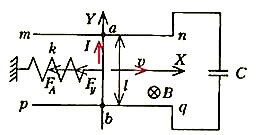
Попробуем создать осциллятор-кентавр, состоящий из конденсатора и пружины (назовем его Ck-осциллятор). На рисунке 1 представлена его принципиальная схема. В электрическую цепь конденсатора емкостью С входит проводник ab длиной l, который может свободно двигаться без трения вдоль неподвижных проводников mn и pq, сохраняя с ними электрический контакт. Проводник ab находится в однородном магнитном поле с индукцией, равной В и направленной перпендикулярно плоскости рисунка (от читателя). К нему прикреплена пружина жесткостью к. Будем считать, что массы всех движущихся частей пренебрежимо малы, а сопротивление в цепи конденсатора равно нулю. При движении проводника ab вдоль mn и pq со скоростью υ на его концах возникает ЭДС индукции

\(~\varepsilon_i = Bl \upsilon\) .

Поскольку сопротивление в цепи конденсатора отсутствует, ЭДС индукции должна равняться разности потенциалов на обкладках конденсатора:

\(~\frac qC = Bl \upsilon\) . (1)

где q — заряд конденсатора. С другой стороны, если по ab идет ток I (обусловленный силой Лоренца), то на проводник со стороны магнитного поля действует сила Ампера, равная

\(~F_A = -BlI\)

(знак «минус» определяется правилом левойруки) Учитывая также силу упругости \(~F_y = -kx\) со стороны пружины, второй закон Ньютона для ab запишем в виде

\(~ma = -BlI - kx\) .

По предположению m = 0, т.е.

\(~BlI = -kx\) . (2)

Продифференцируем левую и правую части уравнения (1) по времени:

\(~\frac 1C q' = Bl \upsilon'\) . (3)

Так как q’ = I, a υ’ = x, из (2) и (3) получаем

\(~x'' + \frac{k}{C(BL)^2} x = 0\) .

Это уравнение гармонических колебаний нашего Ck-осциллятора, частота которых равна

\(~\omega_{Ck} + \frac{1}{BL} \sqrt{\frac kC}\) .

Рис. 2

Рассмотрим еще один осциллятор-кентавр, состоящий из катушки индуктивностью L и груза массой М, связанного с проводником, движущимся в магнитном поле (рис.2). Легко убедиться, что в этом случае для электрической цепи уравнение принимает вид \(~LI' = Bl \upsilon\), a второй закон Ньютона для груза —

\(~Mx'' = -BlI\) .

Отсюда получаем

\(~I'' + \frac{(Bl)^2}{ML} I = 0\) ,

т.е. частота LM-осциллятора равна

\(~\omega_{LM} + \frac{BL}{\sqrt{ML}} \) .

В осцилляторах-кентаврах могут наблюдаться те же виды колебаний, что и в чисто механических или чисто электрических колебательных системах. Например, если, предварительно зарядив конденсатор (или растянув пружину), предоставить Ck-осциллятор самому себе, то в нем возникнут свободные колебания. Если же в цепь конденсатора включить ЭДС, изменяющуюся по гармоническому закону (или приложить к ab гармоническую силу), то возникнут вынужденные колебания.

Оценим величины ω_Ck и ω_LM. Для этого выберем практически разумные значения для соответствующих параметров. Пусть, например, В = 10^-2 Тл, I = 0,1 м, С = 10^-4 Ф, k = 1 Н/м, L = 10^-2 Гн, М = 10^-2 кг . Тогда ω_Ck = 10⁵ с^-1 и ω_LM = 10^-1 с^-1. Понятно, что 10⁵ с^-1 — неприемлемая частота для колебаний пружины. С другой стороны, 10^-1 с^-1 — малое значение для частоты тока, текущего по соленоиду. Очевидно, мы имеем дело с несовместимостью электрических и механических частей. Чтобы преодолеть эту несовместимость, необходимо определенное искусство (на рисунках 1 и 2 представлены не действующие установки, а принципиальные схемы, выражающие общую идею). В частности, необходимо увеличивать С и уменьшать k в Ck-осцилляторе, уменьшать L и М в LM-осцилляторе. В обоих случаях необходимо увеличивать Bl и уменьшать сопротивления — электрическое и механическое. Например, для увеличения длины l проводника ab можно изготовить его в виде катушки, совершающей крутильные колебания в магнитном поле, т.е. в качестве Ck- осциллятора использовать высокочувствительный зеркальный гальванометр, к выходу которого подсоединить конденсатор с большой емкостью.

Если в вашем школьном физическом кабинете имеется зеркальный гальванометр, то вы можете провести такой опыт. Подсоедините ко входу гальванометра фотоэлемент. При освещении фотоэлемента световой указатель гальванометра отклонится и покажет наличие в цепи тока. После выключения осветителя фотоэлемента начнутся свободные колебания рамки гальванометра. По движению светового указателя определите период крутильных колебаний рамки. Повторите опыт, предварительно подсоединив ко входу гальванометра параллельно фотоэлементу конденсатор большой емкости (5·10² - 10³ мкФ). Если период колебаний рамки при этом значительно увеличится, то это будет означать, что вы наблюдаете электромеханические колебания Ck-осциллятора.