Kvant. Обжегшись на молоке

Стасенко А.Л. Обжегшись на молоке, на воду дуют... //Квант. — 2010. — № 3. — С. 42-43

По специальной договоренности с редколлегией и редакцией журнала "Квант"

И, видно, неспроста. но чем это объяснить?

Наверное, многим знаком невольный эксперимент: быстро вынув палец из кипятка, хочется на него подуть или помахать рукой (лучше не пробуйте повторить этот эксперимент). Ясно, что тут речь идет об усилении теплоотвода от пальца в воздух. Физики давно научились описывать этот процесс. Считается, что плотность потока тепловой энергии j_т , измеряемая в Дж/(м² · с), в направлении некоторой координаты r пропорциональна скорости изменения (точнее, темпу изменения) температуры в противоположном направлении:

\(j_t \sim \frac{\Delta T}{\Delta r}\ .\ \ \ \ \ \ \\)(1)

Здесь Δr - расстояние между двумя точками среды, температуры которых отличаются на ΔT . А знак «минус» говорит о том, что тепло течет от горячих участков к холодным. Отношение \(\frac{\Delta T}{\Delta r}\) называют градиентом температуры вдоль r, а сама зависимость (1) есть закон Фурье - по имени французского физика и математика Жана Батиста Фурье (1768-1830).

Но, оказывается, такая пропорциональность встречается не только в теории теплопроводности. Например, плотность

электрического тока j_э , измеряемая в А/м² = Кл/(м² · с) , пропорциональна градиенту электрического потенциала ф , который непосредственно определяет напряженность электрического поля \(\vec E\) :

\(j_e \sim \frac{\Delta \phi}{\Delta r} = E_r \ . \ \ \ \ \ (2)\)

Этот закон называется (обобщенным) законом Ома, по имени немецкого физика Георга Симона Ома (1787-1854). Сравнивая выражения (1) и (2), можно и температуру Т назвать потенциалом - разность значений этого потенциала вызывает поток тепла.

Далее, если в каком-либо растворе, например сахара в воде или духов в воздухе, концентрация вещества неодинакова в разных точках, то возникает диффузия, и плотность потока молекул этого вещества j_n оказывается пропорциональной градиенту концентрации n, т.е. темпу ее изменения в пространстве:

\(j_n \sim \frac{\Delta n}{\Delta r}\ \ \ \ \ \ \ (3)\)

Это соотношение - закон Фика, в честь немецкого физиолога Адольфа Фика (1829-1901). Теперь можно и концентрацию вещества назвать потенциалом, разность значений которого вызывает диффузионный поток массы.

Но и это еще не все. Когда мы дуем на палец, скорость потока воздуха у его поверхности близка к нулю, а с удалением от поверхности она возрастает. Иными словами, имеет место изменение касательной составляющей скорости по направлению нормали Δu/Δr . В результате возникает касательное напряжение j_u , измеряемое в Н/м² , т.е. трение слоев воздуха друг о друга и, в конечном счете, о саму поверхность обтекаемого тела. И, оказывается,

\(j_u \sim -\frac{\Delta u}{\Delta r}.\ \ \ \ \ \ \ \ (4)\)

А ведь это напряжение можно назвать плотностью потока импульса: Н/м² = (кг · м/с))(м² · с)! Сравнивая выражение (4) с предыдущими, как не назвать скорость потенциалом? Жидкости, подчиняющиеся этому закону, называются ньютоновскими. Вы догадались, почему? Правильно: его установил великий Ньютон еще в 1687 году.

Теперь можно удивиться и восхититься: различные по своей природе физические процессы, описание которых более чем 100-300 лет назад предложено замечательными учеными разных стран, отражают некий общий факт: плотность потока любой физической сущности - тепловой энергии, электрического заряда, растворимого вещества, импульса... пропорциональна темпу пространственного изменения соответствующего потенциала - температуры, электрического напряжения, концентрации, скорости.

Все упомянутые процессы называются явлениями переноса. Знак пропорциональности в приведеных соотношениях можно заменить знаком равенства, если при каждом градиенте написать соответствующий коэффициент: теплопроводности, электропроводности, диффузии, вязкости. - это хорошо знают студенты уже первого курса университета.

Однако вернемся к обваренному кипятком пальцу. Кто же переносит тепло от пальца и почему хочется на него подуть? Конечно, этим занимаются молекулы, и, конечно, дуновение ускоряет теплоотвод.

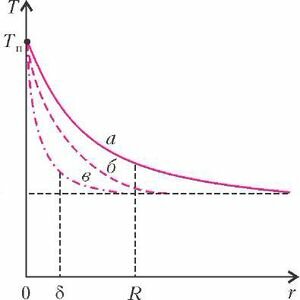
Рассмотрим сферу (или полусферу) радиусом R с температурой поверхности Т_п , моделирующую кончик пальца. Если окружающий воздух спокоен, «горячие» молекулы, тепловая скорость которых соответствует Т_п , проталкиваются в направлении от поверхности (рис.1,а), а навстречу им также проталкиваются холодные молекулы из «бесконечности», где температура равна T_∞ . Устанавливается некоторое распределение температуры, которое качественно представлено кривой а на рисунке 2. Можно показать, что температура падает в радиальном направлении довольно плавно, по гиперболическому закону, существенно изменяясь на расстоянии порядка R. (В этих рассуждениях не принята во внимание сила Архимеда, заставляющая всплывать теплый газ в атмосфере холодного и, конечно, помогающая отводу тепла.) В результате плотность потока тепловой энергии от поверхности можно записать в виде зависимости от конечной разности температур и расстояния, на котором происходит ее существенное изменение:

\(j_a \sim -\frac{T_p - T_\infty}{R}.\)

Рис. 1

Теперь начнем потихоньку дуть на палец. Ясно, что молекулы, уносящие тепло, «сдуваются» потоком воздуха (рис.1,б). Наконец, подуем что есть силы, тогда все молекулы, «стартующие» от поверхности, уместятся в тонком слое характерной толщины 8 (рис.1,е), существенно меньшей радиуса сферы R (δ << R) . (Соответствующие этим случаям графики распределения температуры качественно представлены кривыми б и е на рисунке 2.) В результате поток тепла увеличится:

\(j_b \sim \frac{T_p - T_\infty}{\sigma} \gg \frac{T_p - T_\infty}{R} \sim j_a \ .\)

Рис. 2

Этот тонкий слой называют пограничным. Он был впервые введен известным немецким аэродинамиком Людвигом Прандтлем (1875-1953) - конечно, не в применении к пальцу, а при решении проблем сопротивления тел в потоке жидкости или газа. Есть мнение, что только за введение этого плодотворного понятия Прандтлю следовало бы присудить Нобелевскую премию.

Но продолжим наши рассуждения. Мы знаем, что именно молекулы уносят тепло от пальца (и приносят «холод» из окружающей среды). Значит, для оценки толщины теплового погранслоя следует использовать характеристики молекулярного хаоса. Какие именно? Разумеется, прежде всего это средняя скорость теплового движения \(\langle c \rangle\) - чем быстрее движутся молекулы, тем интенсивнее теплообмен. Далее, это средняя длина свободного пробега молекулы l - чем она больше, тем дальше унесет молекула энергию, передав ее следующей молекуле при столкновении. Произведение этих двух величин имеет размерность м²/с , а если его умножить на время прохождения воздухом характерного расстояния порядка радиуса R, то получим оценку квадрата толщины погранслоя:

\(\sigma^2 \sim \langle c \rangle l \frac{R}{u} \sim \langle c \rangle l t.\ \ \ \ \ \ \ \ (5)\)

(Кстати сказать, именно Фурье первым стал применять метод размерностей.)

Соотношение (5) характерно для всех процессов блуждания. Оно восходит к первым попыткам описания броуновского движения частиц. А его образным аналогом является проблема пьяного матроса в незнакомом городе. Оказавшись на любом перекрестке, матрос наугад выбирает одно из четырех направлений. Спрашивается: как далеко матрос уйдет от начальной точки, пройдя N кварталов? Ответ: средний ожидаемый квадрат этого удаления пропорционален N. Понятно, что удаление δ будет зависеть и от скорости движения \(\langle c \rangle\), и от длины кварталов l, т.е. будет описываться выражением (5). Осталось подставить его в формулу для плотности потока тепла от поверхности пальца:

Отсюда видно, что от нас зависит только скорость потока воздуха u. Именно она превращает медленную диффузию молекул на дне погранслоя в быстрый конвективный перенос на его внешней границе. Так что дуйте посильнее. Но не переусердствуйте. Ибо если достичь сверхзвуковой скорости, то, наоборот, большая кинетическая энергия потока воздуха перейдет в точке торможения в тепло и даст высокую температуру поверхности. Действительно, из закона сохранения энергии

\(\frac{Mu^2_\infty}{2} + \frac{5}{2} RT_\infty = 0 + \frac{5}{2}RT_p \ ,\)

записанного для одного моля воздуха, при скорости обдува, например, u_∞ = 1000 м/с получим

\(T_p = T_\infty + \frac{Mu^2_\infty}{2} = 300K + \frac{0,029 \cdot 10^6}{5 \cdot 8,31} K \approx 1000K !\)

Впрочем, едва ли наши губы и легкие позволят обеспечить сверхзвуковое обтекание пальца воздухом.

Интересно заметить, что при ковке знаменитых сабель из дамасской стали кузнец вручал джигиту раскаленный клинок и джигит немедленно скакал во весь опор, усиленно размахивая им. По-видимому, такой режим охлаждения был оптимальным для тогдашней инновационной технологии.

Но все ли мы учли? Нет, не все: палец-то после кипятка мокрый! И тут вступает в силу еще процесс испарения молекул воды, за которым следует их диффузия в погранслое и унос воздухом. Для описания этого процесса нужно использовать соотношение (3). Нам это не в новинку - ведь и рассмотренная ранее теплопроводность есть не что иное как диффузия тепловой энергии. И теперь к отводу тепла молекулами воздуха добавится унос теплоты фазового перехода L вместе с испаряющейся массой воды:

\(j_mL \sim \frac{n_p - n_\infty}{\sigma} \ .\)

Здесь j_m = j_nm (m - масса молекулы) - это плотность потока массы, уносимой с обдуваемого тела, n_п и n_∞ -соответствующие значения концентрации молекул воды. Этот унос тепла максимален, если окружающий воздух сухой ( n_∞ → 0 ). И это значительная добавка - ведь удельная теплота парообразования для воды достаточно велика: L ≈ 2 МДж/кг .

Вот почему для охлаждения летательных аппаратов, входящих в атмосферу с большой скоростью, используют жидкость, продавливаемую изнутри через пористую поверхность тела: испаряясь, она уносит тепло и спасает аппарат от сгорания. Не напрасно также в жарких пустынях для охлаждения пепси ставят бутылку, обернутую мокрой тряпкой, на крышу автомобиля и гонят его как можно быстрее. Тут уж работают и u, и L, и...

Вот как полезно знать газотермодинамику!