Kvant. Наклоная плоскость
А так ли хорошо знакома вам наклонная плокость? // Квант. — 2009. — № 5. — С. 32-33.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
...если у вас имеется плоская поверхность, совершенно
гладкая, как зеркало, а из вещества твердого, как сталь, не
параллельная горизонту, но несколько наклонная, и если вы
положите на нее совершенно круглый шар из вещества тяжелого
и весьма твердого, например из бронзы, то что, думаете вы, он
станет делать, будучи предоставлен самому себе?
...повторяя опыты сотни раз, мы постоянно находили, что
отношение пройденных путей равно отношению квадратов
времен их прохождения при всех наклонах плоскости...
Степени скорости, приобретаемые одним и тем же телом при
движении по разным наклонным плоскостям, равны между
собой, если высоты этих наклонных плоскостей одинаковы.
Тела, опускающиеся по дугам, соответствующим хордам,
наклоненным к горизонту..., совершают движение, как
показывает опыт, также в равные промежутки времени и притом
меньшие, нежели движение по хордам.
Галилео Галилей
Тело, падающее по наклонной плоскости, . движется
несвободно, так как находящаяся внизу плоскость. препятствует
телу падать прямо, как этого требует сила тяжести.
Леонард Эйлер
Силы, возникающие при движении частицы вниз по склону под
действием тяжести, весьма и весьма запутаны.
Ричард Фейнман
Что собой представляет наклонная плоскость — объект наблюдений, прибор для проведения опытов, простой механизм? И то, и другое, и третье — потому и стала персонажем «Калейдоскопа», тем более что открытие основополагающих законов механики трудно представить без ее участия. Великий Галилей, с которого и началось современное естествознание, сумел сделать ее надежным помощником в своих экспериментах и выводах, о чем можно судить по числу упоминаний о ней в его трудах, что лишь малой частью отражено в эпиграфе.
Конечно, наклонные плоскости применяли еще строители египетских пирамид, поднимая с их помощью каменные блоки массой в две с половиной тонны на высоту в полтораста метров. Но эти плоскости — неотъемлемая часть и сегодняшней нашей жизни. Принцип их действия используется в любом винтовом устройстве, начиная от шурупов и кончая навинчиваемыми крышками банок и бутылок. А как обойтись без знаний о наклонных плоскостях при строительстве автомобильных и железных дорог, в особенности на пересеченной или горной местности, при проектировании фуникулеров и эскалаторов, при прокладке горнолыжных спусков и возведении трамплинов, при организации аттракционов или оборудовании пандусов для инвалидов, при исследовании сползания ледников и схода лавин?..
Множество примеров лишь подтверждают важность обращения к этому простому механизму, «простота» которого, по мнению Фейнмана, не так очевидна, как кажется, в чем мы призываем убедиться и вас.
Вопросы и задачи
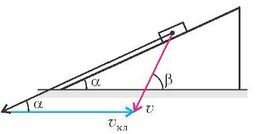
- Скорость монеты, соскальзывающей с клина, изображена на рисунке. Графическим построением найдите скорость клина.
- Из верхней точки вертикального диска прорезан желоб, составляющий угол а с вертикальным диаметром диска. Как зависит время скольжения грузика по желобу от угла а, если трением можно пренебречь?
- Под каким углом к вертикали должен быть направлен из точки, находящейся над наклонной плоскостью, гладкий желоб, чтобы шарик соскользнул по нему на плоскость за наименьшее время?
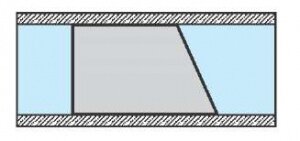
- В прямоугольной трубке находится поршень, форма которого в сечении представлена на рисунке. Давление жидкости по обе стороны поршня в горизонтально расположенной трубке одинаково. Будет ли поршень находиться в равновесии?
- Две мензурки одинаковой длины заполнены водой, одна расположена вертикально, другая — под углом 30° к горизонту. Как будут различаться давления воды на дно мензурок?
- На доску положили два одинаковых кирпича — один плашмя, а второй на ребро. Какой кирпич соскользнет с доски первым (если при этом он не опрокидывается), когда доску станут наклонять?
- Брусок находится на шероховатой плоскости, угол наклона которой можно изменять от 0 до 90°. Что при этом будет происходить с силой трения, действующей на брусок, если пренебречь явлением застоя?
- На наклонной плоскости с углом наклона а покоится монета массой m. С какой силой реакции наклонная плоскость действует на монету? Чему равна при этом сила трения?
- На клин, плоскость которого составляет угол а с горизонтом, положили небольшое тело. Какое ускорение надо сообщить клину в горизонтальном направлении, чтобы тело свободно падало?
- На наклонной плоскости лежит монета, удерживаемая силой трения. Как она будет двигаться, если ей сообщить горизонтальную скорость вдоль плоскости?
- Какой силой F можно удержать на месте брусок массой m, лежащий на гладкой наклонной плоскости с углом при основании а ?
- Математический маятник укреплен на тележке, скатывающейся без трения с наклонной плоскости. Найдите положение равновесия маятника.
- Левый клин медленно вдвигают под правый, отношение катетов в котором представлено на рисунке. Каким должен быть угол а, чтобы правый клин перевернулся?
- При каком условии винт может служить для крепления деталей?
- С вершины сортировочной горки поочередно скатывают два вагона: один пустой, другой груженый. Какой вагон проедет дальше по прямолинейному участку после скатывания с горки?
- Если автомобиль въезжает на гору при неизменной мощности двигателя, то его скорость движения уменьшается. Почему?
- Цилиндр, диаметр которого равен его высоте, один раз соскальзывает с наклонной плоскости вдоль своей образующей, а другой раз скатывается с той же точки плоскости. Сравните поступательные скорости цилиндра у основания наклонной плоскости, считая коэффициент трения скольжения между цилиндром и плоскостью очень малым
- В кузове грузовика находятся три одинаковых гладких бревна, расположенных, как показано на рисунке. На какой угол а может накрениться кузов, чтобы верхнее бревно не скатилось на борт?
Микроопыт
Склейте цилиндр из плотной бумаги (можно взять картонную втулку от рулона туалетной бумаги) и закрепите на его внутренней стороне кусок пластилина. Такой цилиндр может катиться вверх по наклонной плоскости. Как этого добиться?
Любопытно, что...
...наиболее гениальным изобретением Архимеда был водоподъемный винт. По оценке Галилея, это устройство«не только великолепно, но просто чудесно, поскольку мы видим, что водаподнимается в винте, беспрерывно опускаясь». Архимедов винт использовался,например, в Египте как для подъема воды на возвышенности (на высоту до 4метров), которых обычно разлив Нила не достигал, так и для осушения низменныхместностей.
...со временпоследователей Архимеда — Герона и Паппа — механику стали считать наукой опростых машинах: вороте, рычаге, блоке, клине и винте. Два последних основанына свойствах наклонной плоскости, закон действия которой, правда, самомуАрхимеду известен не был.
...изучая равновесиезамкнутой цепочки, наброшенной на две наклонные плоскости, голландский ученыйСимон Стевин в своей работе «Начала статики» доказал, что сила, скатывающаягруз, во столько же раз меньше его веса, во сколько раз высота плоскости меньшеее длины.
...в трактате,составленном в период чтения им публичных лекций в 1597—1598 годах, Галилей,не зная еще закона разложения сил, рассматривал сначала рычаг, затем сводил крычагу клин, к клину — наклонную плоскость, а к наклонной плоскости — винт.
...законы свободного падения тел Галилей устанавливал с помощью наклонной плоскости — желоба, оклеенного изнутри полированным пергаментом, применяя еедля «уменьшения» ускорения свободного падения в заданное число раз...
...разбирая движениепо плоскости, которая «ни вниз не опускается, ни вверх не поднимается», Галилей выявил свойство тел сохранять свою скорость, хотя еще не нашел полной и точной формулировки закона инерции, что предстояло сделать Ньютону.
...исследуя перекатывание шара «с горки на горку», Галилей предположил, что, говоря современным языком, приобретаемая при спуске скорость не зависит от формы пути, по которому движется тело. Галилей, естественно, не знал, что такое положение вытекает из закона сохранения энергии, однако он этот закон предчувствовал и применял в простейших случаях падения тела или движения по наклонной плоскости и в опытах с маятником.
...Галилей геометрическим методом построил теорию движения по наклонной плоскости идвижения по хордам круга, показав, что по дуге круга, которая меньше или равна четверти окружности, тело соскальзывает быстрее, чем по стягивающей хорде.Этим он предвосхитил постановку задачи о поиске линии быстрейшего спуска —брахистохроны, задачи, решенной в 1697 году Иоганном Бернулли. Уравнение этойкривой, оказавшейся циклоидой, используется, кстати, при проектировании санных трасс и «американских» горок.
...при завинчивании болта с шагом резьбы в 1 миллиметр с помощью гаечного ключа длиной 30 сантиметровмы выигрываем в силе в две тысячи раз, что либо позволяет надежно скреплять детали, либо легким усилием передвигать большие тяжести.
...чтобы автомобили не вылетали на поворотах, дороги в этих местах делают наклонными. Правильный угол наклона соответствует радиусу поворота и определенной скорости движения, на которую необходимо устанавливать ограничение. А вот велосипедные треки имеют наповоротах переменный наклон — в расчете на различные скорости, достигаемые спортсменами.
Что читать в «Кванте» о наклонной плоскости
(Публикации последних лет)
- «Комбинированные задачи по механике» — 2003, Приложение №6, с. 92;
- «О динамике криволинейного движения» — 2005, №2, с. 30;
- «Центр масс механической системы» - 2006, №2, с. 25;
- «Какая горка самая быстрая»?» - 2006, Приложение №6, с. 68;
- «И тележка в гору едет.» - 2008, №5, с. 35;
- «Подводные камни» силы Архимеда» — 2009, №2, с. 46.
Материал подготовил А.Леонович
Ответы
- См. рис.2.
- Поскольку ускорение грузика пропорционально длине желоба, время движения по любому желобу, прорезанному по хорде диска, будет одним и тем же.
- Нужно построить окружность, проходящую через данную точку А и касающуюся плоскости с заданным углом наклона \(~\alpha\) в некоторой точке А', а центр этой окружности должен лежать на вертикали под точкой А (рис.3). Тогда движение по желобу, расположенному по прямой AA' под углом \(~\alpha / 2\) к вертикали, будет происходить за кратчайшее время (см. решение задачи 2).
- Поршень будет находиться в равновесии, так как проекции сил давления жидкости на ось трубки слева и справа равны.
- Давление жидкости определяется глубиной, отсчитываемой по вертикали, исходя из чего в первой мензурке давление воды на дно будет в два раза больше, чем во второй.
- Кирпичи начнут скользить одновременно, так как действующие на них силы трения равны - они не зависят от размеров трущихся поверхностей.
- До определенного угла \(~\alpha_0\) (расчет дает значение \(~ tg \alpha_0 = \mu ,\) где \(~\mu\) - коэффициент трения скольжения) растет сила трения покоя, удерживающая брусок на плоскости, при дальнейшем увеличении угла на брусок действует сила трения скольжения, убывающая до нуля при достижении \(~90^\circ .\)
- \(\vec R = -m\vec g, F_{tr} = mg \sin \alpha .\)
- Начав свободно падать, тело за некоторое время сместится по вертикали на высоту \(~h,\) пропорциональную ускорению \(~g\) (рис. 4). За то же время клин должен сместиться в горизонтальном направлении не менее чем на перемещение \(~s,\) пропорциональное ускорению \(~a\) (см. заштрихованный треугольник на рисунке). Учитывая, что \(~s/h = ctg\alpha ,\) получаем \(~\alpha = g ctg\alpha .\)
- Как только монета получит указанную скорость, сила трения окажется направленной противоположно ей. Так как эта сила горизонтальна, то она не сможет препятствовать движе-нпю монеты вниз по наклонной плоскости. В результате монета станет двигаться по кривой, изображенной на рисунке 5.
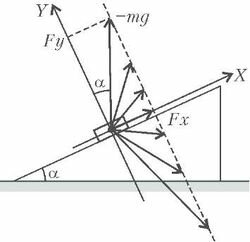
- \(~F_x = mg \sin \alpha , F_y \le mg \cos \alpha \)(см. рис. 6).
- Поскольку маятник находится на тележке, скатывающейся с наклонной плоскости с ускорением \(~a = g \sin \alpha ,\) его положение равновесия будет таким, при котором маятник движется относительно плоскости с тем же ускорением, что и тележка. На рисунке 7 видно, что это возможно, лишь когда нить маятника перпендикулярна наклонной плоскости.
- \(~tg \alpha > 0,75 .\)
- Для таких винтов выполняется неравенство \(~2\pi r \gg h ,\) где \(~r\) и \(~h\) - радиус и шаг винта соответственно.
- Одинаково, если не учитывать сопротивление воздуха; второй вагон, если сопротивление учитывать.
- При движении в гору необходимо увеличить силу тяги, а при постоянной мощности двигателя это возможно лишь при уменьшении скорости автомобиля.
- При выполнении указанного в задаче условия скорость цилиндра у основания плоскости в первом случае больше, так как во втором случае часть потенциальной энергии цилиндра будет преобразована в кинетическую энергию вращения.
- Верхнее бревно (2) останется в равновесии при \(~\alpha < 30^\circ .\) В противном случае направление силы тяжести этого бревна пройдет левее точки опоры о нижнее бревно (1), и верхнее бревно скатится на борт.
Микроопыт
Надо разместить цилиндр на наклонной плоскости так, как показано на рисунке 8, тогда он будет вести себя подобно игрушке «Ванька-встанька», когда момент силы тяжести относительно точки опоры заставляет фигурку разворачиваться, взбираясь вверх. Необходимо учесть, что при больших углах наклона плоскости цилиндр может начать проскальзывать по ней.