Kvant. Металлы
Эдельман В. Металлы //Квант. — 1992. — № 2. — С. 2-9.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Что такое металлы?
«Металлом называется светлое тело, которое ковать можно»,— писал в 1763 году Ломоносов. Загляните в ваш учебник химии и вы увидите, что металлы обладают характерным металлическим блеском («светлое тело»), хорошо проводят тепло и электрический ток. Правда, тут же вы прочтете, что существуют элементы, проявляющие свойства как металлов, так и неметаллов. Другими словами, нет четкой грани, отделяющей одно от другого. Химика, который интересуется, в первую очередь, химическими реакциями и для которого каждый элемент — свой особый мир, такая неоднозначность не очень смущает. А вот физика это не устраивает. Если физика делит тела на металлы и неметаллы, то нужно понять, в чем их принципиальное различие. Поэтому надо так определить, что такое металл, чтобы, как и в других случаях в области точных наук, удовлетворить двум требованиям:
- все металлы должны обладать всеми без исключения приписываемыми им признаками;
- иные объекты должны не обладать хотя бы одним из этих признаков.
Вооружившись этими соображениями, посмотрим, все ли металлы без исключения имеют все свойства, приписываемые им учебником. Начнем с «ковать можно», т. е. с пластичности, говоря современным языком. И тут же, по созвучию, мы вспомним пластмассы: ведь не зря они так названы, многим из них свойственна пластичность — способность необратимо изменять форму без разрушения. Конечно, медь, железо, алюминий ковать легко, со свинцом еще проще, индий — довольно редкий и дорогой металл — можно мять почти как воск (а воск ведь — не металл!), щелочные металлы и того мягче. А попробуйте стукнуть по обычному чугуну — и он разлетится на кусочки! Ну, тут металлурги скажут: это потому, что чугун — не простое вещество. Он состоит из кристаллов железа, разделенных прослойками углерода, т. е. графита. Вот по этим-то прослойкам чугун и ломается. Ну что же, все верно. Только вот беда — хрупкий графит, как оказывается, современная физика относит к металлам! Да и не один графит: числятся, например, среди металлов мышьяк, сурьма и висмут, но ковать их можно с таким же успехом, как стекло — разлетаются на мелкие кусочки!
Проделайте такой простой опыт: разбейте баллон сгоревшей лампы, достаньте оттуда вольфрамовую спираль и попробуйте ее раскрутить. Ничего не выйдет, она рассыпется в пыль! Но ведь как-то ее сумели скрутить на заводе? Значит, может быть и такое — то можно деформировать, то нельзя, в зависимости от того, что происходило с образцом в прошлом. Что ж, придется, видимо, с этим признаком — пластичностью — расстаться. Тем более, что он присущ многим неметаллам; ведь то же стекло — нагрей его, и оно станет мягким и податливым.
Итак, укорачиваем формулировку и двигаемся дальше.
На очереди — «блеск», или, говоря научным языком, оптические свойства. Блестящих предметов много: и вода, и стекло, и полированные камни, да мало ли что еще. Так что просто «блеском» не обойтись, вот и говорится: для металлов характерен металлический блеск. Ну, это совсем хорошо: получается, что металл — это металл. Правда, интуитивно мы чувствуем, что металлическим блеском блестят полированные медь, золото, серебро, железо. А широко распространенный минерал пирит — разве не блестит, как металлы? Про типичные полупроводники германий и кремний и говорить не приходится, по внешнему виду их от металлов никак не отличишь. С другой стороны, не так давно научились получать хорошие кристаллы таких соединений, как двуокись молибдена; кристаллы эти коричнево-фиолетовые и на обычный металл мало похожи. Оказывается, это вещество надо считать металлом. Почему — будет ясно чуть дальше.
Так что блеск как чисто «металлический» признак отпадает.
На очереди — теплопроводность. Пожалуй, этот признак можно отбросить сразу — все без исключения тела проводят тепло. Правда, про металлы говорится, что они хорошо проводят тепло. Но, боюсь, на вопрос «что такое хорошо и что такое плохо?» в этом случае ни один папа не ответит.
Хорошо ли проводит тепло медь? Посмотрим в таблицу и сразу же столкнемся со встречным вопросом: а какая медь и при какой температуре? Если взять чистую медь, например ту, из которой делают провода для радиоприборов, и нагреть ее до красного каления, т. е. отжечь, то при комнатной температуре она да еще чистое серебро будут проводить тепло лучше любого другого металла. Но погните такой медный образец, стукните или зажмите в тисках — и его теплопроводность станет заметно хуже. А что произойдет, если кусочек отожженной меди начать охлаждать? Сначала теплопроводность будет расти, увеличится в десятки раз при температуре около 10 К, а потом начнет быстро падать и при достижении абсолютного нуля должна стать нулевой (рис. 1).
Возьмем теперь другой металл — висмут. Картина для него очень похожа на ту, которую мы видели для меди, только максимум теплопроводности лежит при 3 К, а при комнатной температуре висмут проводит тепло плохо, не многим лучше, чем кристалл кварца. Но кварц-то — не металл! И тот же кварц, как видно из рисунка 1, по своим теплопроводным свойствам иногда оказывается не хуже меди. А плавленный кварц, т. е. кварцевое стекло, проводит тепло плохо, примерно как нержавеющая сталь.
Кварц — не исключение. Все кристаллы хорошего качества ведут себя подобным образом, только числа будут немного различными. У алмаза, например, уже при комнатной температуре теплопроводность лучше, чем у меди.
Отбрасываем с чистым сердцем теплопроводность и жалеть об этом не будем. И не только потому, что по этому признаку металл от неметалла не так уж легко отличить, но и потому, что, оказывается, специфические черты в теплопроводности металлов (а такие есть) являются следствием его электропроводности — последнего оставшегося свойства.
И опять в формулировке, приведенной в начале статьи, уточнение — не просто электропроводность, а хорошая электропроводность. А ведь когда речь шла о теплопроводности, эпитет «хорошая» нас насторожил и, как оказалось, не напрасно. Что же — и последнее свойство под подозрением? Надо обязательно его спасать, а то мы останемся вообще без металлов, а заодно без полупроводников, без изоляторов. Вот это наука получается! Любой школьник в большинстве случаев не задумываясь скажет, с чем он имеет дело, а копнули поглубже — остановились в недоумении.
И есть от чего. Возьмем таблицы физических величин и посмотрим на числа. Вот, к примеру, при комнатной температуре удельное сопротивление ρ (Ом·см) меди ~1,55·10-6; у висмута ρ ~ 10-4; у графита ρ ~ 10-3; у чистых кремния и германия ρ ~ 102 (но, добавляя примеси, его можно довести до ~10-3); у мрамора ρ = 107 - 1011; у стекла ρ = 1010; а где-то в конце списка — янтарь с удельным сопротивлением до 1019. И где же тут кончаются металлы-проводники и начинаются диэлектрики? А мы еще не упомянули про электролиты. Обычная морская вода неплохо проводит ток. Что же — и ее считать металлом?
Посмотрим, не поможет ли нам температура. Если повышать температуру, то различия между веществами начнут сглаживаться: у меди сопротивление начнет расти, у стекла, например, уменьшаться. Значит, надо проследить за тем, что произойдет при охлаждении. И вот тут мы наконец увидим качественные различия. Посмотрите на рисунок 2: при температурах жидкого гелия, вблизи абсолютного нуля, вещества разделились на две группы. У одних сопротивление остается небольшим, у сплавов или у не очень чистых металлов ρ почти не изменяется при охлаждении, у чистых металлов сопротивление сильно уменьшается. Чем чище и совершеннее кристалл, тем значительнее это изменение. Иногда ц при температуре, близкой к абсолютному нулю, меньше, чем при комнатной, в сотни тысяч раз. У других веществ, например у полупроводников, с понижением температуры сопротивление начинает стремительно возрастать, и чем ниже температура, тем оно больше. Бели бы можно было добраться до абсолютного нуля, то ρ стало бы бесконечно большим. Впрочем, достаточно и того, что сопротивление реально становится столь большим, что никаким современным прибором его уже не измеришь.
Итак, мы добрались до ответа: металлы — это такие вещества, которые проводят электричество при любой температуре.
В противоположность этому диэлектрики перестают проводить ток, если их охладить до абсолютного нуля. Если пользоваться таким определением, то и графит, и двуокись молибдена оказываются металлами. А куда же отнести полупроводники? Если речь идет о чистых, совершенных кристаллах, то они, строго говоря, диэлектрики. Но если в них содержится много примесей, то они могут стать металлами, т. е. сохранять проводимость при самых низких температурах.
Что же у нас осталось в конце концов? Нам удалось выявить единственный существенный признак, руководствуясь которым мы можем, если не в повседневной практике, то хотя бы в принципе, всегда отличить металл от неметалла. А раз этот признак единственный, то оказываются автоматически удовлетворенными оба условия, выполнения которых мы потребовали в начале статьи.
Почему металлы проводят ток?
Уже давно было замечено, что одни элементы, такие как медь, золото, серебро, железо, свинец, олово, и в чистом виде, и при сплавлении друг с другом образуют металлы. Другие, например фосфор, сера, хлор, азот, кислород, не только сами металлами не являются, но и соединяясь с металлами превращают их в диэлектрики. Пример тому — обыкновенная соль NaCl. Поэтому в химии появилось деление элементов на металлы и неметаллы.
Такая классификация, однако, не более чем констатация фактов, хотя на первый взгляд она претендует на то, чтобы объяснить свойства веществ исходя только из строения атомов. В самом деле, посмотрим на таблицу Менделеева. Элементы, расположенные в одном столбце, очень похожи по своим химическим свойствам. А вот будут ли изготовленные из них кристаллы или сплавы проводить электрический ток? Глядя на таблицу, ответить на этот вопрос нельзя. Так, все элементы первой группы — металлы, за исключением первого — водорода. Но ведь закон, который кому-то разрешено нарушать,— уже не закон. Правда, во второй группе дело обстоит лучше: здесь все элементы — привычные металлы; а в третьей группе опять сбой: бор — полупроводник, а алюминий — прекрасный металл. Дальше еще хуже. Первый элемент четвертой группы — углерод; мы уже упоминали, что графит, так называют кристалл углерода,— это металл. А вот алмаз — тоже кристалл, составленный из атомов углерода, но расположенных иначе, чем в графите,— изолятор. Кремний и германий — классические полупроводники. Олово — казалось бы, типичный металл. Однако... Если всем знакомое белое блестящее олово долго подержать при температуре -30 °С, то его кристаллическая структура изменится, а внешне оно посереет. И это олово — его так и называют «серое олово» — полупроводник! А свинец всегда металл.
Если начинать смешивать разные элементы, то картина совсем усложнится. Возьмем, например, и сплавим два металла индий и сурьму — в пропорции один к одному. Получим широко применяемый в технике полупроводник InSb. С другой стороны, мы уже говорили, что двуокись молибдена МoО2 при Т ≈ 0 К проводит ток, т. е. МoО2 — металл. (И WО2, и Re2О3 и некоторые другие оксиды — тоже металлы.) А если получающиеся из атомов кристаллы сильно сжать, сдавить, то, оказывается, чуть ли не все вещества становятся металлами, даже такие типичные металлоиды, как сера. Правда, для нее давление перехода в металлическое состояние очень велико — несколько сотен тысяч атмосфер (а для водорода еще больше).
Похоже, что разделить элементы на металлы и неметаллы — не такая уж простая задача. Во всяком случае, ясно, что, рассматривая отдельные атомы, мы не можем сказать, будет ли вещество, составленное из этих атомов, проводить ток при Т ≈ 0 К, потому что огромную роль играет то, как расположены атомы друг относительно друга. Поэтому для ответа на вопрос «почему металлы проводят ток?» надо изучать, как атомы взаимодействуют между собой, образуя твердое тело.
Посмотрим, как обстоит дело с простейшим из металлов — литием. Порядковый номер Li — три. Это означает, что ядро атома Li содержит три протона и положительный заряд ядра компенсируют три электрона. Два из них образуют заполненную s-оболочку, ближайшую к ядру, и сильно связаны с ядром. Оставшийся электронрасположен на второй s-оболочке. На ней мог бы поместиться еще один электрон, но его у лития нет. Все остальные разрешенные состояния энергии свободны, и электроны на них попадают только при возбуждении атома (например, при сильном нагреве паров лития). Схема уровней в атоме лития показана на рисунке 3.
Рассмотрим теперь множество атомов лития, находящихся в ограниченном объеме. Они могут образовывать газ (пар), жидкость или твердое тело. При достаточно низкой температуре силы взаимного притяжения препятствуют тепловому движению атомов, образуется кристалл. Это наверняка происходит при абсолютном нуле температуры, когда все известные вещества, кроме гелия,— кристаллы.
Итак, из опыта известно, что при низких температурах твердое тело — устойчивое состояние для лития. Но, как известно, устойчивым всегда является такое состояние вещества, в котором его внутренняя энергия меньше, чем в других возможных агрегатных состояниях при той же температуре. Суммарное уменьшение энергии при переходе из одного состояния в другое легко измерить — ведь это и есть теплота испарения или плавления.
С микроскопической точки зрения при низких температурах внутренняя энергия вещества есть, в первую очередь, сумма энергий электронов атомов, составляющих тело. Но электроны в атомах занимают строго определенные уровни энергии. Значит, мы можем ожидать, что при сближении атомов изменятся уровни энергии. При этом распределение электронов по уровням должно оказаться таким, чтобы их суммарная энергия была меньше, чем сумма энергий электронов в таком же количестве изолированных друг от друга атомов.
Что произойдёт с уровнями, можно понять исходя из аналогии движения электрона в атоме с любой колебательной системой, например с маятником. Пусть у нас есть два совершенно одинаковых маятника. Пока они не взаимодействуют друг с другом, частота колебаний обоих маятников одна и та же. Введем теперь взаимодействие между ними — свяжем их, например, мягкой пружинкой. И сразу же вместо одной частоты появятся две. Посмотрите на рисунок 4: связанные маятники могут колебаться синфазно, а могут навстречу друг другу. Очевидно, в последнем случае их движение будет более быстрым, т. е. частота колебаний такой системы выше собственной частоты колебаний одного маятника. Таким образом, связь приводит к расщеплению частот. Если связать три маятника, то станет уже три собственных частоты, у системы из четырех связанных маятников четыре собственные частоты и так далее до бесконечности.
Поведение любой другой колебательной системы подобно. Если мы заменим маятники, например, на электрические колебательные контуры, то, как хорошо знают радиолюбители, при введении связи между ними их собственные частоты также расщепляются. Электроны в атоме — это тоже своеобразная колебательная система. Как и маятник, электроны имеют массу, есть сила Кулона, возвращающая их к положению равновесия; и этим определяется движение электронов в атоме, характеризуемое, согласно квантовой механике, собственной частотой. Для электронов включение взаимодействия при взаимном сближении приводит к тому, что частоты, бывшие до того одинаковыми, становятся немного разными.
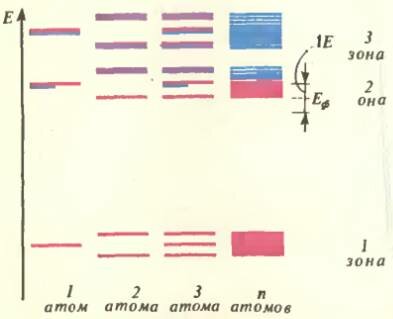
В квантовой механике имеется прямая связь между энергией и частотой колебаний, выражаемая формулой \(~E = h \nu\), где h = 6,6·10-34 Дж·с — постоянная Планка, а ν — частота колебаний. Поэтому надо ожидать, что при сближении двух атомов лития каждый из уровней, показанных на рисунке 3, расщепится на два. Каждому новому уровню энергии будет соответствовать своя электронная оболочка теперь уже не отдельного атома, а «молекулы». Оболочки заполняются электронами по тому же правилу, что и у атома,— по два электрона на оболочку. Та пара оболочек, которая получилась из самого нижнего уровня, будет полностью заполнена электронами. Действительно, на них можно разместить четыре электрона, а их у двух атомов лития — шесть. Остаются два электрона, которые теперь расположатся на нижнем из уровней второй пары. Заметьте, какой произошел качественный скачок: раньше эти два электрона занимали два из четырех состояний, имеющих одинаковую энергию. Теперь у них появилась возможность выбирать, и они расположились так, чтобы их суммарная энергия была поменьше. Нетрудно сообразить, что произойдет при добавлении следующих атомов: для трех атомов каждый исходный уровень расщепится на три (см. рис. 3). Девять электронов расположатся так: шесть на нижней триаде уровней, возникших из уровня ближайшей к ядру внутренней заполненной оболочки атома; еще два электрона — на нижнем уровне следующей триады; оставшийся электрон — на среднем уровне той же триады. Еще одно место на этом уровне остается свободным, а верхний уровень полностью пуст. Если взять n атомов (\(~n \gg 1\)), то каждый уровень расщепится на n тесно расположенных уровней, образующих, как говорят, полосу или зону разрешенных значений энергии. В нижней полосе все состояния заняты, а во второй — только половина, и именно те, энергия которых ниже. Следующая полоса — полностью пустая.
Расстояние между соседними уровнями в зоне легко оценить. Естественно считать, что при сближении атомов изменение энергии электронов атома примерно равно теплоте испарения вещества, пересчитанной на один атом. Она составляет для металлов обычно несколько электронвольт, а значит, и полная ширина зон ΔE, определяемая взаимодействием соседних атомов, должна иметь тот же масштаб, т. е. ΔE ~ 1 эВ ≈ 10-19 Дж. Для расстояния между уровнями получим \(~\delta E \sim \dfrac{\Delta E}{n}\), где n — число атомов в образце. Это число чрезвычайно велико: межатомное расстояние составляет всего несколько ангстремов, и объем, приходящийся на один атом, оказывается всего ~ 10-22 см3. Если наш образец имеет, для определенности, объем 1 см3, то для него n ≈ 1022. Поэтому численно оказывается δE ≈ 10-22 · ΔE ≈ 10-41 Дж. Эта величина столь мала, что всегда можно пренебречь квантованием энергии внутри зоны и считать, что в пределах зоны разрешены любые значения энергии.
Итак, в кристалле уровни энергии размываются в зоны, имеющие ширину, сравнимую с расстоянием между ними. Разрешенными для электронов являются состояния внутри зоны, и здесь электроны могут иметь практически любую энергию (разумеется, в пределах ширины зоны). Но очень важно, что число мест в каждой зоне строго ограничено и равно удвоенному числу атомов, составляющих кристалл. И это обстоятельство, совместно с принципом минимума энергии, определяет распределение электронов по зонам. Теперь у нас все готово, чтобы наконец понять, почему литий проводит ток. Взглянем опять на рисунок 3. Что же получилось? Пока атомы были сами по себе, все электроны находились во вполне определенных состояниях, строго одинаковых для всех атомов. Теперь атомы объединились в кристалл. Сами атомы в кристалле не только одинаковы, но и совершенно одинаково расположены относительно соседей (за исключением, конечно, тех, которые попали на поверхность кристалла). А все электроны имеют теперь разные энергии. Это может быть только в том случае, если электроны больше не принадлежат отдельным атомам, а каждый электрон «поделили» между собой все атомы. Другими словами, электроны свободно передвигаются внутри идеального кристалла, образуя как бы жидкость, которая заполняет весь объем образца. И электрический ток — это направленный поток этой жидкости, аналогичный текущей по трубам воде.
Чтобы заставить воду течь по трубе, надо создать разность давлений у концов трубы. Тогда под действием внешних сил молекулы приобретут направленную скорость — вода потечет. Очень важно здесь появление именно направленной скорости, ведь сами по себе молекулы хаотически движутся с громадными скоростями — при комнатной температуре средняя скорость теплового движения молекулы порядка 103 м/с. Так что дополнительная энергия, приобретаемая молекулой в потоке, мала по сравнению с энергией теплового движения.
Дополнительная энергия, которую надо сообщить электрону, чтобы он участвовал в общем направленном движении электронов в кристалле (а это и есть ток), также мала по сравнению с собственной энергией электрона. В этом нетрудно убедиться. Мы уже говорили, что энергия электрона по порядку величины равна 1 эВ = 1,6·10-19 Дж. Если вспомнить, что для свободного электрона \(~E = \dfrac{m \upsilon^2}{2}\) и m = 9,1·10-31 кг, то легко найти скорость: υ ~ 106 м/с. Предположим, что все электроны участвуют в токе, а их в 1 м3 проводника n ~ 1028 Z (Z — заряд ядра). Тогда в проводе с поперечным сечением S = 10-6 м2 при токе I ≈ 10 А (при большем токе провод расплавится) направленная скорость электронов равна \(~\upsilon_H = \dfrac{I}{neS} \approx 10^{-2} - 10^{-3}\) м/с. Значит, энергия электрона, участвующего в токе, больше энергии Е свободного электрона всего на 10-8 Е, т. е. на 1,6·10-27 Дж.
И тут мы сталкиваемся с удивительным фактом: оказывается,электроны, которые расположены в нижней зоне, называемой обычно валентной, не могут изменить свою энергию на малую величину. Ведь если какой-то электрон увеличит свою энергию, то это значит, что он должен перейти на другой уровень, а все соседние уровни в валентной зоне уже заняты. Свободные места есть только в следующей зоне. Но чтобы туда попасть, электрон должен изменить свою энергию сразу на несколько электрон-вольт. Вот так и сидят электроны в валентной зоне и ждут журавля в небе — энергичного кванта. А кванты нужной энергии бывают у видимого или ультрафиолетового света.
Итак, жидкость есть, а течь она не может. И если бы у лития было всего два электрона в атоме, т. е. если бы мы строили картинку для атомов лития, то получили бы мы изолятор. Но твердый гелий — действительно изолятор, так что мы можем уже поздравить себя с некоторым успехом: мы еще не объяснили, почему в металлах может течь ток, зато поняли, почему диэлектрики, где электронов полным-полно и все они «размазаны» по всему кристаллу, не проводят ток.
А что же литий? Да ведь у него есть вторая зона, которая заполнена только наполовину. Энергию, разделяющую занятые и свободные уровни внутри этой зоны, называют энергией Ферми Eф. Как мы уже говорили, разность энергий между уровнями в зоне очень невелика. Электрону, который расположен в зоне возле уровня Ферми, достаточно чуть-чуть увеличить свою энергию — и он на свободе, там, где состояния не заняты. Электронам из приграничной полосы ничто не мешает увеличить энергию под действием электрического поля и приобрести направленную скорость. А ведь это и есть ток! Но так же легко этим электронам и потерять направленную скорость, столкнувшись с атомами-примесями (которые всегда есть) или с другими нарушениями идеальной структуры кристалла. Этим объясняется сопротивление току.
Кажется, ясно, почему гелий — изолятор, а литий — проводник. Попробуем-ка наши представления применить к следующему элементу — бериллию. И тут — осечка, модель не сработала. У бериллия — четыре электрона, и, казалось бы, должны быть полностью заняты первая и вторая зоны, а третья обязана быть пустой. Получается изолятор, в то время как бериллий — металл.
Дело вот в чем. Если ширина зон достаточно велика, то они могут налезть друг на друга. Про такое явление говорят, что зоны перекрываются. У бериллия так и происходит: минимальная энергия электронов в третьей зоне меньше, чем максимальная во второй. Поэтому электронам оказывается энергетически выгодно оставить пустой часть второй зоны и занять состояния внизу третьей. Вот и получается металл.
А что будет с другими элементами? Перекрываются зоны или нет, заранее сказать нельзя, для этого нужны громоздкие расчеты на ЭВМ, и то не всегда можно получить достоверный ответ. Но вот что примечательно: из нашей схемы следует, что если брать элементы с нечетным числом электронов, то всегда должен получаться металл, если только структурной единицей в кристалле является отдельный атом. А вот водород, например, азот и фтор не желают кристаллизоваться в такую решетку. Они предпочитают сначала объединиться попарно, а уже молекулы, содержащие по четному числу электронов, выстраиваются в кристалл. И законы квантовой механики не мешают ему быть диэлектриком.
Итак, мы теперь знаем, что такое металл с точки зрения физики, и разобрались в самой сути явления, поняв, почему в принципе существуют изоляторы и проводники. Мы увидели, что нельзя предложить простой способ объяснения, почему какое-то конкретное вещество оказалось диэлектриком или металлом. Сделать это можно, лишь вооружившись всей мощью аппарата современной квантовой механики и вычислительной техники, но это уже задача специалистов.