Kvant. Магнитная катушка
Мягмарсурэн С. Как исследовать магнитную катушку //Квант. — 2005. — № 3. — С. 31,34-35.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Обсудим один из возможных методов измерения магнитной индукции и энергии магнитного поля катушки.
Энергию магнитного поля катушки индуктивности можно определить, используя взаимные преобразования энергии: электрической-магнитной-тепловой-электрической. Соберем установку, электрическая схема которой показана на рисунке 1. В качестве индукционной катушки мы использовали электромагнит, состоящий из дроссельной катушки и сердечника с двумя полюсными наконечниками, повернутыми плоскими сторонами друг к другу. При замыкании ключа K в положение 1 ток I проходит по катушке индуктивностью L, за счет чего в катушке образуется ЭДС самоиндукции \(~\varepsilon_i = -L \frac{dI}{dt}\) . Согласно правилу Кирхгофа,
Здесь R — сумма сопротивления реостата и омического сопротивления катушки. За время dt источник электрической энергии совершает работу, равную
Первое слагаемое в этой формуле выражает тепло Джоуля-Ленца, которое выделяется на сопротивлении R, а второе — дополнительную работу, обусловленную явлением самоиндукции. Следовательно, дополнительная работа, расходуемая на увеличение тока в цепи от 0 до значения I, является энергией магнитного поля W:
А теперь замкнем ключ в положение 2 — в правой цепи ток самоиндукции I проходит через омическое сопротивление Rk и сопротивление резистора Rr, на которых и выделяются количества теплоты Qk и Qr соответственно. Таким образом, энергия, запасенная в магнитном поле катушки, переходит в электрическую, а затем в тепловую.
Согласно закону сохранения энергии,
В этом выражении сопротивления Rk и Rr есть известные и точно измеряемые параметры. Поэтому для определения W нам придется узнать величину Qr.
Используем уравнение теплового баланса:
где m — масса материала, имеющего сопротивление Rr, c — удельная теплоемкость того же материала, ΔT — изменение его температуры. Величину ΔT измеряют термопарой ТП — для этого измерительный контакт прибора прикрепляется внутри витков резистора сопротивлением Rr, а другой, сравнивающий, контакт поддерживают при комнатной температуре T0 (см. рис.1). Температурная разность контактов термопары ΔT прямо пропорциональна межконтактной разности потенциалов, т.е. термо-ЭДС εT. С учетом этого факта получим
где δ — чувствительность термопары, измеряемая в милливольтах на кельвин.
Если выбрать сопротивление резистора Rr значительно больше, чем сопротивление катушки Rk, то эффект преобразования магнитной энергии в тепловую хорошо прослеживается. Поэтому в качестве резистора используют проволочную спираль, сделанную из сплава с большим удельным сопротивлением. В подавляющем большинстве случаев для такого металлического сплава удельная теплоемкость неизвестна, так что нам придется определить эту величину. Для этого мы придумали маленькую хитрость.
Соберем электрическую схему — такую же, как на рисунке 1, только без катушки индуктивности. Резистор, по которому течет ток I’ в течение времени t, нагревается, и в нем выделяется некоторое количество теплоты. Если при этом не возникает никаких других форм энергии, то, по закону сохранения энергии,
Используя ту же термопару, определим новое изменение температуры\[~\Delta T' = \frac{\varepsilon'_T}{\delta}\]. Поэтому можно записать
В этом выражении ε’T пропорционально времени t (с момента включения ключа K до окончания измерения). Величины I’, ε’T, t экспериментально измеряются. Таким образом, во второй части опыта можно определить удельную теплоемкость с для любых электропроводящих материалов.
Используя выражения для количества теплоты Qr и удельного сопротивления c, для энергии магнитного поля получим
где А — постоянная прибора, которая равна
На самом деле, энергия магнитного поля является функцией двух переменных — силы тока I и расстояния между полюсами электромагнита d. Для определения энергии магнитного поля в зазоре электромагнита нами экспериментально построены графики зависимости термо-ЭДС от силы тока при разных значениях d (рис.2). Из графиков видно, что зависимость εT (I) — квадратичная. Значит, зависимость термо-ЭДС от квадрата тока будет линейной. Таким образом, для нашего прибора получаются вольт-амперные характеристики вида εT (I,d) = K(d) I2, а их коэффициенты K(d) являются, в свою очередь, функцией d. Это приводит к следующему выражению для W:
где коэффициент AK(d), согласно формуле \(~W = \frac{LI^2}{2}\) , будет выражать индуктивность катушки L, точнее \(~\frac L2\).
Наконец, используя вольт-амперные характеристики, построим градуировочный график зависимости K(d) (рис.3). Такая градуировка и представляет собой измеритель энергии магнитного поля, создающегося в данном электромагните при любых значениях силы тока и расстояния между его полюсами. А последнее выражение для W(I,d) является эмпирически полученной нами формулой (основанной на опыте) для определения магнитной энергии данного электромагнита.
Теперь приступим к определению магнитной индукции поля. Разделив выражение для W(I,d) на объем воздушного зазора между полюсами электромагнита, получим объемную плотность магнитной энергии (всеми нежелательными краевыми эффектами мы будем пренебрегать):
где S — площадь поперечного сечения полюса электромагнита. С другой стороны, объемная плотность магнитного поля прямо пропорциональна квадрату магнитной индукции В в данном месте пространства:
где μ — относительная магнитная проницаемость вещества, μ0 — магнитная постоянная. Из сопоставления двух после- дних выражений следует, что магнитная индукция и сила тока связаны соотношением
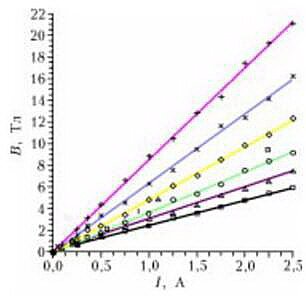
Поскольку для данного электромагнита градуировка K(d) уже установлена, можно графически построить семейство зависимости B(I,d) (рис.4). Из полученных графиков магнитная индукция непосредственно определяется без измерения и без вычисления при разных значениях либо d, либо I. Таким образом, мы получили эмпирическую формулу и создали градуировочные кривые для определения индукции магнитного поля.