Kvant. Кинематика

Стасенко А.Л. Кинематика, да и только //Квант. — 1992. — № 11. — С. 32-35.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Как известно, векторы перемещения, скорости и ускорения — важнейшие понятия кинематики. Попробуем расширить их круг.

Пусть, например, движение происходит вдоль некоторой координаты l_|| Договоримся перемещение измерять в м_||, а скорость \(~\upsilon_{||} = \frac{\Delta l_{||}}{\Delta t}\) — в м_||/с. Теперь умножим скорость на площадь поперечного сечения S_⊥. Размерность величины υ_||S_⊥ будет м_||м²_⊥/c, или попросту м³/с (правда, в этой последней записи уже потеряна информация о том, что чему параллельно или перпендикулярно). При этом мы получим очень полезную вещь — единицу измерения объемного расхода. Это может быть, скажем, расход воды в реке или в ванне. В физике такие величины называют потоками. В принципе можно построить поток любого вектора (механического, электрического, магнитного), но в рассмотренном конкретном случае мы получили чисто кинематическое понятие, так как в него входят только пространственно-временные характеристики движения — скорость и площадь поперечного сечения.

А что, если скорость умножить на перемещение вдоль той же координаты, по которой происходит движение: υ_||l_||? Получим нечто, измеряемое в м²_||. Ничего особенного, казалось бы. Однако это новое понятие становится особенно полезным, когда движение происходит по замкнутой траектории, например по окружности радиусом r. Тогда величина (тоже кинематическая) υ_||l_|| где l_|| = 2 πr, приобретает собственное имя: циркуляция скорости.

Такие движения — их обычно называют вихревыми — часто встречаются в природе — например, смерчи, торнадо, тайфуны; их можно наблюдать при сливе воды из раковины, иногда можно увидеть, как закручивается дымок выхлопной струи за автомобилем или любоваться цветными струями дымовых шашек за крыльями самолетов на авиапарадах.

Рис. 1

Мы рассмотрим здесь простейший из вихрей, в котором величина скорости, направленной в каждой точке по касательной к окружности, обратно пропорциональна ее радиусу\[~\upsilon = \frac{\Gamma}{2 \pi r}\], где буква Г и обозначает эту самую циркуляцию. Посмотрим, как в поле скоростей такого вихря деформируется какая-нибудь фигура, например первоначально (в момент времени t = 0) имевшая вид круга с центром в точке О и радиусом r₀ (рис. 1).

Все точки очень тонкой полоски, принадлежащей кругу и заключенной между двумя очень близко расположенными дугами с радиусами r и r + Δr с общим центром на оси вихря С (эта полоска закрашена), имеют одну и ту же скорость, так что ни длина, ни форма этой полоски со временем изменяться не будут. В моменты времени t₁, 2t₁, …, когда радиус СО повернется на угол φ₁, 2φ₁, …, эта полоска будет занимать положения, изображенные на рисунке тоже в виде закрашенных участков.

Точки всех других дуговых полосок будут двигаться по окружностям тоже с неизменными, но другими скоростями. Например, точка В будет двигаться быстрее, а точка А — медленнее закрашенной полоски, |υ_A| < |υ_B|. По кривой вверху рисунка можно узнать величину скорости каждой точки такой полоски и, поскольку угол ее поворота вокруг С пропорционален скорости, построить положения центров всех полосок в моменты времени t₁, 2t₁, …

Диаметр АОВ нашего круга теперь будет принимать вид кривых А₁О₁В₁, А₂О₂В₂, …, а окружность (которой принадлежат концы полосок) — вид некоторых замкнутых кривых, длина которых будет расти со временем.

Можно сказать и так: поскольку в поле вихря скорость каждой точки обратно пропорциональна ее расстоянию r до центра вихря С, за некоторое время каждая точка опишет дугу, длина которой тоже обратно пропорциональна этому расстоянию (модулю своего радиуса-вектора r). Но, как известно, центральный угол прямо пропорционален длине своей дуги и обратно пропорционален ее радиусу. В результате за одно и то же время радиус-вектор каждой точки повернется на угол, обратно пропорциональный квадрату ее расстояния от центра\[~\varphi \sim \frac{t}{r^2}\].

Очевидно, что площадь, ограниченная этими замкнутыми кривыми, будет оставаться неизменной и равной \(~\pi r^2_0\) (Для собственного удовольствия_вы можете перед сном рассмотреть, как поле вихря деформирует любую другую замкнутую фигуру — квадрат, треугольник, вашу фотографию.)

Что мы описали таким образом? Ну, например, этот круг можно считать начальным сечением струи двигателя самолета, попавшей в поле вихря, образовавшегося у конца крыла (см. статью «Самолет в озоне» — «Квант», 1992, № 5 и 6). Тогда линия АОВС на рисунке 1 идет вдоль правого крыла самолета — при виде сзади.

Конечно, тут мы не рассмотрели еще один процесс — диффузию струи, которая будет приводить к дополнительному «расплыванию» первоначально круглого сечения. И еще не рассмотрели второй вихрь, с осью С’, расположенный слева. А это попробуем сделать, учитывая, что он то же создает поле скоростей, обратно пропорциональных по величине расстоянию до этого вихря, и используя принцип суперпозиции.

Рис. 2

Применим этот принцип для точек, лежащих в плоскости симметрии между двумя вихрями (рис. 2). Прежде всего, если расстояние между вихрями l, то каждый вихрь будет создавать в том месте, где расположен второй вихрь, скорость \(~\upsilon_k = -\frac{\Gamma}{2 \pi l}\) (ведь сам на себя вихрь не действует). Значит, "оба вихря будут «топить» друг друга в воздухе с этой постоянной скоростью, а их ординаты будут линейно меняться со временем:

\(~y_k = - |\upsilon_k| t\) .

В точках плоскости симметрии два вихря создадут суммарную скорость, направленную вертикально вниз (горизонтальные компоненты уничтожаются) и равную

\(~\upsilon_y = \frac{\Delta y}{\Delta t} = -2 \frac{\Gamma}{2 \pi r_C} \cos \alpha\) ,

где \(~r_C = \sqrt{\left(\frac l2\right)^2 + \eta^2} ; \eta = y - y_k ; \cos \alpha = \frac{\frac l2}{r_C}\) , или

\(~\frac{\Delta y}{\Delta t} = -2 \frac{\Gamma \frac l2}{2 \pi \left( \left(\frac l2\right)^2 + (y + |\upsilon_k| t)^2\right)}\) .

Правая часть этого уравнения зависит сразу и от y, и от t, и хотя для компьютера это не затруднение, но для нашего анализа это неудобно. Поэтому «пересядем» в систему координат, связанную с движущимися вихрями (поскольку они опускаются с постоянной скоростью, такая «пересадка» не приведет к появлению каких- либо дополнительных сложностей — обе системы инерциальны). Это равносильно вычитанию вертикальной скорости υ_k, так что в новой системе вертикальная составляющая скорости \(~\upsilon_{\eta} = \frac{\Delta \eta}{\Delta t}\)будет равна

\(~\upsilon_{\eta} = \upsilon_y - \upsilon_k = \frac{\Gamma}{2 \pi l} \left( 1 - \frac{l^2}{\left(\frac l2\right)^2 + \eta^2} \right) = |\upsilon_k| \frac{\eta^2 - 3 \left(\frac l2\right)^2}{\eta^2 + \left(\frac l2\right)^2}\) .

Проанализируем дробь в правой части этого уравнения как функцию расстояния η между горизонтальной линией СС’, соединяющей центры вихрей, и рассматриваемой точкой с координатой y в плоскости симметрии. Видно, прежде всего, что эта функция симметрична относительно значения η = 0: изменение знака η не изменяет значения этой функции. В точке η = 0 дробь принимает значение \(~\frac{\upsilon_{\eta}}{|\upsilon_k|} = -3\). В двух точках \(~\pm \eta_* = \pm \frac{\sqrt 3}{2} l\) она равна нулю. При всех |η| < η_* дробь отрицательна, при |η| > η_* — положительна. При очень больших значениях \(~|\eta| >> \frac l2\) она стремится к единице. Соответствующая кривая изображена на рисунке 3.

Рис. 3

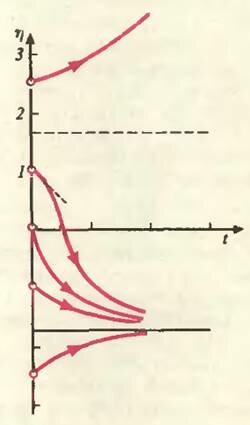
Теперь качественно проанализируем изменение ординаты η со временем (рис. 4). Если в начальный момент времени t = 0 значение η лежит внутри интервала от —η_* до +η_*, например в точках, соответствующих D или D’, то скорость υ_η при этом отрицательна и в обоих случаях ордината с течением времени будет стремиться к значению —η_*. Если при t = 0 окажется, что |η| > η_*, (например, для точек Е и Е’), то скорости υ_η будут положительными, только из Е’ значение координаты η стремится к —η_*, а из Е — уходит от η_*. Можно сказать, что точка —η_* «притягивает» к себе траектории, а точка +η_*, «отталкивает», и потому положение струи здесь неустойчиво. Впрочем, оказывается, все струи в плоскости симметрии неустойчивы, но это уже другой разговор.

Рис. 4

В порядке тренировки попробуйте перерисовать кривые, изображенные на рисунках 3 и 4, для y(t), т. е. вновь перейти в систему координат, связанную с самолетом, а не с вихрями.

Итак, только кинематика — как и было обещано.