Kvant. Ионосфера и цунами

Стасенко А. Ионосфера и шум цунами//Квант. — 2009. — № 5. — С. 36-37

По специальной договоренности с редколлегией и редакцией журнала "Квант"

"Поднялась к небу волна высоты неизмеримой, закрыла грудью половину неба и, качая белым хребтом, согнулась, переломилась, упала на берег и страшной тяжестью своею... смыла весь берег" (М.Горький). Таково художественное описание катастрофических явлений, время от времени происходящих у берегов теплых стран и уже унесших жизни сотен тысяч людей.

Но при чем тут ионосфера, расположенная на высоте порядка сотен километров над землей и морем? А вот послушайте.

Вспомним, как объясняют поведение вещества, попавшего во внешнее постоянное электрическое поле с напряженностью \(~\vec E_0 .\) Пусть имеется плоский слой вещества, состоящего из частиц с положительными и отрицательными зарядами в равных количествах, так что этот слой в целом электрически нейтрален. И пусть он находится в электрическом поле, перпендикулярном плоскостям этого слоя. Под действием поля положительные заряды сместятся в направлении вектора \(~\vec E_0 ,\) отрицательные - в противоположном направлении, так что на обеих плоскостях слоя возникнут поверхностные заряды, которые породят вторичное поле \(~\vec E_1 ,\) противоположное по направлению полю \(~\vec E_0 \) (рис.1). Это, так сказать, нормальное поведение вещества, поляризованного внешним полем. Его состояние можно описать такими макроскопическими характеристиками, как диэлектрическая проницаемость \(~\varepsilon\) и коэффициент преломления \(~n\). Обе эти величины больше единицы. В случае вакуума они равны единице.

рис. 1

Теперь посмотрим, что произойдет, если внешнее электрическое поле изменяется во времени, например по синусоидальному закону

\(~E = E_m \sin \omega t .\) (1)

Здесь \(~E_m\) - амплитуда, \(~\omega = 2\pi/T\) - круговая частота колебаний поля, Т - период колебаний. Конкретизируем вещество - пусть оно состоит из электронов и положительно заряженных ионов, т.е. представляет собой плазму. Как известно, самый легкий из ионов (протон) почти в две тысячи раз тяжелее электрона, поэтому переменное электрическое поле будет заметно смещать в течение периода только электроны, и о ионах можно не думать - они нужны только для того, чтобы вещество в среднем (в пространстве и в течение периода) оставалось электронейтральным.

Второй закон Ньютона, описывающий динамику электрона в заданном переменном электрическом поле, запишем в виде

\(~a = -\frac{e_0E_m}{m_e}\sin\omega t = \upsilon'_e = x''_e.\) (2)

Здесь a - это ускорение, m_e - масса электрона, e₀ -величина его заряда; знак «минус» учитывает, что сила, действующая на электрон, направлена против поля; в конце строчки формул сделано напоминание, что ускорение есть первая производная от скорости или вторая производная от смещения из положения равновесия (когда x_e = 0 ).

Тот, кто умеет интегрировать, сразу скажет, что для определения смещения по известному гармонически изменяющемуся ускорению нужно последнее умножить на \(~ - 1/\omega^2 =-(T/2\pi)^2 .\)

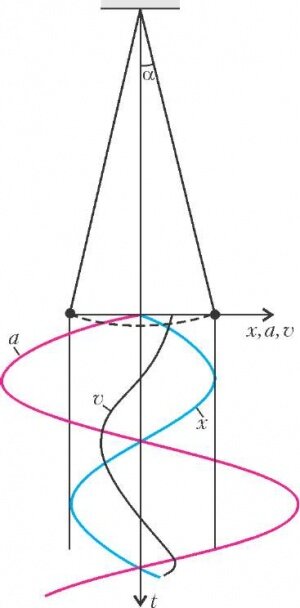
А для того, кто не умеет, достаточно предложить следующую аналогию. Рассмотрим малые колебания грузика массой m на нити длиной l. Этим «грузиком» может вообразить себя Читатель, а «нитью» пусть будут стропы качелей. Нарисуем изменения во времени кинематических характеристик грузика: ускорения а, скорости \(~\upsilon,\) смещения 'xx: (рис.2; ось t направлена вниз). Поскольку колебания гармонические, смещение можно записать в виде

\(~x = x_m \sin \omega t,\)

рис. 2

где x_m - амплитуда малых колебаний, а их частота, как известно, равна \(~\omega = \sqrt{g/l}\) (g - конечно, ускорение поля тяготения). Сила, возвращающая Читателя в положение равновесия, равна

\(~F = -mg\sin\alpha \approx -mg \frac{x}{l},\)

откуда ускорение равно

\(~a = \frac{f}{m} = -\frac{g}{l}x = - \omega^2x,\)

и смещение -

\(~x = -\frac{a}{\omega^2},\) (3)

что и требовалось показать. Тут самое главное - знак «минус», т.е. тот факт, что при колебаниях ускорение направлено противоположно смещению.

Разумеется, тот же результат даст и решение уравнения (2).

Вернемся к нашему веществу, находящемуся в переменном электрическом поле. На рисунке 3 изображена картина

рис. 3

полей и зарядов в тот момент, когда напряженность внешнего электрического поля достигла наибольшего (амплитудного) значения \(~E_m.\) Согласно выражению (3), в этот момент смещение зарядов прямо противоположно той картине (см. рис.1), которая была при стационарном поле. В результате такого разделения зарядов возникает поле \(~\vec E_1,\) усиливающее внешнее поле.

Тут надо ожидать чего-то необычного - и вот оно-таки появляется. А именно, можно ожидать, что, в отличие от электростатики, где диэлектрическая проницаемость и коэффициент преломления больше единицы, тут будет все наоборот\[~\varepsilon < 1, n < 1.\] Но последнее неравенство, согласно определению \(~n = c_0/c ,\) дает значение \(~c > c_0\) - скорость электромагнитной волны в плазме больше, чем в вакууме! Пора кричать «караул» и вызывать милицию, поскольку это противоречит основному постулату современной физики. Но подождем, что будет дальше.

А дальше вспомним, как вводится такая безразмерная макроскопическая характеристика вещества, как \(~\varepsilon\) :

\(~P_e = \varepsilon_0(\varepsilon-1)E.\) (4)

Смысл P_e понятен хотя бы из соображений размерности. Действительно, [\(~\varepsilon\)₀] = Ф/м , [E] = В/м (вспомним привычный плоский конденсатор), тогда

\(~\lceil P_e \rceil = \lceil \varepsilon_0E \rceil = \) = Ф / м \(~\cdot\) В / м = Кл / м² = Кл \(~\cdot\) м / м³

Отсюда видно, что P_e - это объемная плотность электрических диполей. Получается, что, если каждый электрон сместился из положения равновесия на x:, возник электрический диполь с моментом

\(~p_e = -e_0x.\)

А если электронов в единице объема N_e , то общий дипольный момент этой единицы объема будет

\(~N_ep_e = -N_ee_0x = P_e .\)

Записав выражение (3) в виде

\(~x = \frac{a}{\omega^2} = -\frac{F}{m\omega^2} = -\frac{(-e_0E)}{m_e\omega^2},\)

из равенства (4) получим

\(~-\frac{N_ee_0^2E}{\varepsilon_0m_e\omega^2} = \varepsilon_0(\varepsilon-1)E\)

И сократив на E, найдём

\(~\varepsilon = 1 - \frac{N_ee_0^2}{\varepsilon_0m_e\omega^2} < 1\) (5)

Понятно, что при \(~N_e = 0\) (нет ни электронов, ни ионов) имеем \(~\varepsilon = 1 ,\) как и полагается для вакуума. Кроме того, поскольку заряд входит в квадрате, знак его не имеет значения: если каким-то чудом закрепить электроны, то движение ионов даст качественно тот же результат, но гораздо более слабый из-за их большой массы.

Но вот что самое любопытное: существует такое значение частоты внешнего электромагнитного поля, при котором полученная диэлектрическая проницаемость становится равной нулю! Это так называемая плазменная частота:

\(~\omega_p^2 = \frac{N_ee_0^2}{\varepsilon_0m_e}.\) (6)

При этой частоте плазма становится похожей на металл, а от металла электромагнитные волны отражаются. Благодаря этому и было обнаружено существование высотных ионосферных слоев и возможность дальней радиосвязи.

Да, а как же быть с тем, что скорость электромагнитной волны в плазме получилась больше, чем скорость света в вакууме\[~c > c_0\]? Ничего страшного: дело в том, что этот результат получен для случая идеальной гармонической волны, которая, по определению, существовала до возникновения Вселенной и будет существовать вечно. Но такой волны не бывает! Реально существует волновой пакет, ограниченный в пространстве и времени, состоящий из набора волн с различными частотами и, значит, с различными скоростями распространения в плазме. Эти составляющие гармоники, обгоняя друг друга и отставая друг от друга, несут суммарную энергию со скоростью, не превосходящей c₀ , - с так называемой групповой скоростью.

Полученные выше выражения (5) и (6) оказались полезными прежде всего для исследования верхней атмосферы. Из них видно, например, что, изменяя \(~\omega\) , можно найти значение N_e , т.е. концентрацию электронов в ионосфере.

Но при чем здесь цунами - гигантская волна, порождаемая подводным землетрясением? А вот при чем. Длина такой уединенной волны - эти волны называют солитона-ми - порядка десятков и сотен километров (поэтому они и не очень-то заметны в открытом океане). Для такой волны океан, а тем более прибрежные отмели, - мелкие лужи. Поэтому скорость цунами можно оценить по формуле теории «мелкой воды»:

\(~\upsilon = \sqrt{gh} \) (проверьте размерность).

Полагая h ~ 10³ м , получим

\(~\upsilon \sim \sqrt{10 M/c^2 \cdot 10^3 M} = 10^2 M/c\)

- не всякий байкер выжмет такую скорость! Так вот, этот солитон возмущает атмосферу - от него идет мощная акустическая волна. Дойдя до ионосферы, она периодически изменяет концентрацию электронов N_e . А зондируя возмущенную ионосферу при помощи электромагнитных волн, можно за тысячи километров узнать о приближающейся опасности.

Поистине чудесным образом здесь оказались связанными волны различной физической природы!