Kvant. Импульс и энергия

Кикоин А.К. Импульс и кинетическая энергия //Квант. — 1985. — № 5. — С. 28-29.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Одна из основных идей механики состоит в том, что сила, приложенная к телу, есть причина изменения его скорости. Второй закон Ньютона и выражает эту идею:

\(~m \vec a = m \frac{\vec \upsilon_2 - \vec \upsilon_1}{t} = \vec F\) .

В механике используются еще две величины, связанные со скоростью. Это — импульс тела (другое, сейчас почти вышедшее из употребления, название этой величины — количество движения) и кинетическая энергия тела. Импульс тела \(~\vec p\) — векторная величина, равная (по определению) произведению массы тела на его скорость:

\(~\vec p = m \vec \upsilon\) .

Кинетическая энергия E_k тела — скалярная величина, равная (тоже по определению) половине произведения массы тела на квадрат его скорости:

\(~E_k = \frac{m \upsilon^2}{2}\) .

Поскольку и импульс, и кинетическая энергия непосредственно выражаются через скорость тела, а изменение скорости вызывается действующей на тело силой, очевидно, что изменения импульса и кинетической энергии тоже связаны с силой.

Для импульса тела эта связь следует непосредственно из второго закона Ньютона, записанного в виде

\(~\vec p_2 - \vec p_1 = \vec Ft\) (1)

— изменение импульса тела равно произведению силы на время ее действия, то есть импульсу силы («Физика 8», § 50).

Связь кинетической энергии тела с силой выглядит так:

\(~E_{k2} - E_{k1} = Fs \cos \alpha = A\) , (2)

где s — модуль вектора перемещения тела, α — угол между векторами \(~\vec F\) и \(~\vec s\) , а произведение Fs cos α = A — работа действующей на тело силы. Таким образом, эта запись означает, что изменение кинетической энергии тела равно работе приложенной к телу силы («Физика 8», § 55).

Роль импульса и кинетической энергии в описании движения

Различие между величинами \(~\vec p\) и E_k не ограничивается тем, что одна из них векторная, а другая скалярная.

Из равенства (1) видно, что если сила \(~\vec F\) задана, изменение импульса определяется только временем действия силы и не зависит от того, к какому телу она приложена. Любое тело (тело любой массы) под действием данной силы за данное время изменит свой импульс на одну и ту же величину. Даже если бы, например, столкнулись герои басни Крылова «Слон и Моська», то импульс каждого из них изменился бы одинаково.

Равенство (2) говорит о том, что при заданной силе изменение кинетической энергии тела определяется только расстоянием, пройденным телом в направлении действия силы (произведение s cos α — это проекция перемещения на направление силы). Любое тело под действием данной силы на данном расстоянии изменит свою кинетическую энергию на одну и ту же величину.

Таким образом, изменение импульса связано с промежутком времени, необходимым для изменения скорости тела, а изменение кинетической энергии связано с расстоянием, которое тело должно пройти для изменения его скорости (разумеется, при заданной силе).

Другими словами, изменение импульса — это характеристика действия силы - во времени, а изменение кинетической энергии — характеристика действия силы в пространстве.

Еще одно различие между импульсом и кинетической энергией

Пожалуй, самое замечательное свойство импульса тела состоит в том, что общий импульс замкнутой системы тел (то есть векторная сумма импульсов всех тел системы) остается неизменным при любых взаимодействиях и любых движениях тел этой системы. Это — закон сохранения импульса («Физика 8», § 51).

Обладает ли свойством «сохраняться» кинетическая энергия? Рассмотрим простой пример, из которого сразу станет видно, что в этом импульс и кинетическая энергия отличаются друг от друга.

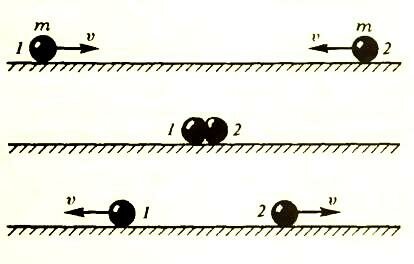
Пусть по гладкой (без трения) горизонтальной поверхности движутся навстречу друг другу с одинаковыми по модулю скоростями υ два одинаковых например стальных, шарика массой m каждый (см. рисунок). В какой-то момент шарики соприкоснутся, затем какое-то время будут продолжать приближаться друг к другу, потом на мгновение остановятся и после этого начнут расходиться, пока не станут двигаться в противоположные стороны с прежними по модулю скоростями.

Посмотрим, чему равны суммарные импульсы и кинетические энергии обоих шариков до, во время и после столкновения.

До столкновения импульсы шариков равны по модулю и противоположны по направлению, поэтому

\(~\vec p_1 + \vec p_2 = (m \vec \upsilon) + (-m \vec \upsilon) = 0\) ,

а кинетические энергии шариков одинаковы и равны \(~\frac{m \upsilon^2}{2}\) каждая, так что

\(~E_{k1} + E_{k2} = \frac{m \upsilon^2}{2} + \frac{m \upsilon^2}{2} = m \upsilon^2\) .

Во время столкновения в тот момент времени, когда оба шарика покоятся, их скорости равны нулю, следовательно,

\(~\begin{matrix} \vec p_1 + \vec p_2 = 0 \\ E_{k1} + E_{k2} = 0 \end{matrix}\) .

После столкновения шарики, как и до столкновения, движутся в противоположные стороны с одинаковыми по модулю скоростями, поэтому

\(~\begin{matrix} \vec p_1 + \vec p_2 = -m \vec \upsilon + m \vec \upsilon = 0 \\ E_{k1} + E_{k2} = \frac{m \upsilon^2}{2} + \frac{m \upsilon^2}{2} = m \upsilon^2 \end{matrix}\) .

Таким образом, суммарный импульс системы двух шариков все время оставался одним и тем же. Кинетическая же энергия до и после столкновения одинакова (именно такое столкновение и называют упругим), а во время столкновения она изменялась, так что в какой-то момент даже временно исчезла совсем. Значит, существует закон сохранения импульса, но нет закона сохранения кинетической энергии.

Заметим, что если бы шарики были не из стали, а из мягкой глины или пластилина, то при столкновении они бы слиплись, остановились и больше бы не двигались (такое столкновение называют абсолютно неупругим). Их общий импульс был бы по прежнему равен нулю, а кинетическая энергия во время столкновения исчезла бы не временно, а навсегда.

Как известно, закон сохранения существует и для энергии, но не для кинетической, а для полной, включающей в себя и другие формы энергии. Так, в нашем примере временная пропажа кинетической энергии при упругом столкновении шариков означает лишь тот факт, что в этот момент она полностью превратилась в потенциальную энергию упругой деформации шариков. В конце столкновения потенциальная энергия вновь целиком превратилась в кинетическую. При неупругом же ударе кинетическая энергия шариков переходит во внутреннюю энергию (шарики нагреваются), которая обратно в кинетическую энергию уже не превращается.