Kvant. Измерение м. поля

Стасенко А.Л. Как Студент магнитное поле измерял //Квант. — 2007. — № 5. — С. 37-39.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Приступив к изучению труда Фарадея, я установил, что его метод понимания явлений был
также математическим, хотя и не представленным в форме обычных математических символов...
Фарадей видел силовые линии, пронизывающие все пространство...
Дж. Максвелл

Как-то на лабораторной работе студент намотал сотни метров проволоки в виде соленоида, да такого длинного, что магнитное поле в его середине можно было считать пространственно однородным, и подключил его к источнику переменного тока с регулируемой частотой ω (рис. 1). И задумался: как бы измерить индукцию магнитного поля?

Рис. 1

Еще в позапрошлом веке было известно, что если через площадь некоторой проводящей рамки, например в виде окружности, со временем изменяется поток вектора магнитной индукции Φ, то в этой рамке возникает электродвижущая сила

\(~\varepsilon = - \frac{\Delta \Phi}{\Delta t}\) .

Таким образом, можно сказать, что ЭДС ε — это скорость изменения потока вектора магнитной индукции через рамку.

Пусть, например, кольцо радиусом r находится в магнитном поле, изменяющемся со временем по гармоническому закону

\(~B = B_0 \cos \omega t\) .

Тогда поток вектора магнитной индукции через площадь кольца будет изменяться по закону

\(~\Phi = \pi r^2 B_0 \cos \omega t\) .

Далее, если рамка проводящая, то ЭДС ε вызовет в ней электрический ток. А можно сказать, что этот ток вызывается напряженностью \(~\vec E\) электрического поля, ускоряющего заряды проводника. Но ЭДС ε связана с напряженностью Ε соотношением

\(~\varepsilon = E \cdot 2 \pi r\) .

Собирая вместе все сказанное, запишем

\(~E \cdot 2 \pi r = - \frac{\Delta (\pi r^2 B_0 \cos \omega t)}{\Delta t}\) .

Более того, и рамка может быть не проводящей, а сделанной, например, из соломинки, через которую пьют сок, — все равно в ней возникнет индукционное электрическое поле. А значит, может и не быть никакой рамки: электрическое поле возникнет и в вакууме, и в воздухе..., которым наполнен соленоид! — догадался Студент. Это поле будет равно

\(~E = - \frac r2 B_0 \frac{\Delta \cos \omega t}{\Delta t} = \frac{rB_0}{2} \omega \sin \omega t\) .

причем оно тоже будет изменяться по гармоническому закону (конечно, тут Студент учел, что скорость изменения косинуса есть минус синус, умноженный на ω).

Но электрическое поле действует на электрический заряд. И тут у Студента возникла идея эксперимента: подвесить внутри соленоида заряженный шарик и измерить амплитуду его колебаний в электрическом поле \(~\vec E\), порожденном переменным магнитным полем \(~\vec B\).

Рис. 2

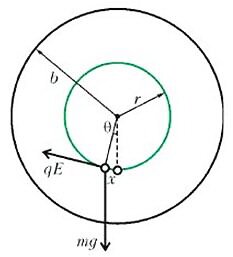
Сказано — сделано. Масса шарика равнялась, конечно, m, его радиус был а, электрический заряд был равен q, а длину нити (разумеется, невесомой, нерастяжимой, бесконечно тонкой) Студент выбрал равной \(~r = \frac b2\), где b — это внутренний радиус соленоида (рис.2). Тогда уравнение движения шарика в электрическом поле E и в поле тяготения с ускорением g приобрело вид

\(~x'' = -g \sin \theta + \frac qm E\) .

Угол отклонения θ этого математического маятника от положения равновесия легко связать со смещением x по окружности\[~\theta = \frac{x}{\frac b2}\]. Кроме того, если рассматривать малые колебания (как и положено здравомыслящему Студенту, а тем более школьнику Отличнику), то вместо синуса можно (приближенно) написать его аргумент (конечно, в радианах)\[~\sin \theta = \theta = \frac{2x}{b}\]. Тогда уравнение колебаний будет выглядеть так:

\(~x'' + \frac{2g}{b} x = \frac qm \frac b2 \frac{B_0}{2} \omega \sin \omega t\) .

Тут еще можно ввести привычное обозначение \(~\frac{2g}{b} = \omega^2_0\), где ω₀ — частота собственных колебаний шарика.

Ба! Ведь это просто уравнение вынужденных колебаний гармонического осциллятора! — воскликнул Студент и немедленно отыскал его решение в виде \(~x = x_0 \sin \omega t\), т.е. тоже гармонических колебаний с частотой вынуждающей силы. Скорость изменения синуса есть косинус, умноженный на ω, а скорость изменения косинуса, как уже было сказано, это минус синус, умноженный на ω. Значит, вместо ускорения х’’ появится \(~-x_0 \omega^2 \sin \omega t\). В результате получится уравнение для определения амплитуды x₀ смещения шарика:

\(~-x_0 \omega^2 \sin \omega t + \omega^2_0 x_0 \sin \omega t = \frac qm \frac{bB_0}{4} \omega \sin \omega t\) .

А поскольку это уравнение должно быть верно для любого момента времени, \(~\sin \omega t\) можно сократить, и останется

\(~x_0 = \frac qm \frac{bB_0}{4} \frac{\omega}{\omega^2_0 - \omega^2}\) .

Но что это? Получилось, что при значении ω = ω₀ знаменатель обращается в ноль, а значит, амплитуда отклонения шарика устремляется в бесконечность (рис. 3; сплошные кривые). Да ведь это резонанс, а с резонансом надо обращаться осторожно. Нужно учесть силу, тормозящую движение шарика, — силу сопротивления воздуха.

Рис. 3

И Студент стал изучать эту силу, роняя мелкие шарики из-под потолка в ванну. На таком большом расстоянии шарик быстро успевал приобрести постоянную скорость \(~\upsilon = \frac ht\), которую легко было вычислить, зная высоту потолка h и замерив секундомером время падения t, а момент падения даже для самых мелких пылинок был заметен на гладкой поверхности воды. В результате этих измерений Студент обнаружил, что сила сопротивления воздуха для мелких шариков пропорциональна их радиусу и скорости движения:

\(~F_s = \gamma a \upsilon = \gamma ax'\) ,

где γ — коэффициент пропорциональности. (Интересно, что еще древний Аристотель указывал на такую зависимость силы от скорости, а в позапрошлом веке ее точно вычислил Стокс для случая медленного, «ползущего» движения сферы в сплошной среде.) Наш Студент получил значение γ = 10^-3/3 Н/(м·м/с) для условий, близких к «нормальным».

В итоге пришлось исправить уравнение движения шарика с учетом найденной силы сопротивления, так что оно приобрело вид

\(~x'' + \omega^2_0 x + \gamma \frac am x'= \frac qm \frac{bB_0}{4} \omega \sin \omega t\) ,

или, для краткости записи,

\(~x'' + \omega^2_0 x + \beta x'= A \omega \sin \omega t\) ,

где

\(~\beta = \gamma \frac am\), \(~A = \frac qm \frac{bB_0}{4}\) .

И тут кончается физика и начинается математика (которая, впрочем, тоже есть часть физики — как считают многие приличные люди). Теперь уже не годится искать решение в прежнем виде \(~x = x_0 \sin \omega t\), и ясно почему: тогда часть слагаемых в левой части по-прежнему будет пропорциональна \(~\sin \omega t\), а вот новое слагаемое, содержащее скорость смещения, будет пропорционально \(~\cos \omega t\), и уравнение нельзя будет сократить ни на \(~\sin \omega t\), ни на \(~\cos \omega t\). Поэтому попробуем искать решение в виде

\(~x = x_0 \cos (\omega t - \varphi)\) ,

где φ — так называемый сдвиг фаз (видно, что при \(~\varphi = \frac{\pi}{2}\) получим прежнее решение).

Подставив эту функцию в наше уравнение, получим

\(~x_0 ((-\omega^2 + \omega^2_0) \cos (\omega t - \varphi) - \beta \omega \sin (\omega t - \varphi)) = A \omega \sin \omega t\) .

Учтем следующие тригонометрические равенства:

\(~\begin{matrix} \cos (\omega t - \varphi) = \cos \omega t \cos \varphi + \sin \omega t \sin \varphi \\ \sin (\omega t - \varphi) = \sin \omega t \cos \varphi - \cos \omega t \sin \varphi \end{matrix}\) .

Тогда в предыдущем уравнении выделятся две группы слагаемых: одна будет содержать \(~\cos \omega t\), другая \(~\sin \omega t\). А поскольку это уравнение должно быть верным в любой момент времени, то коэффициенты при \(~\cos \omega t\) и \(~\sin \omega t\) должны быть равны нулю. Так получим два уравнения для неизвестных x₀ и φ:

\(~\begin{matrix} (-\omega^2 + \omega^2_0) \cos \varphi + \beta \omega \sin \varphi = 0 \\ x_0((-\omega^2 + \omega^2_0) \sin \varphi - \beta \omega \cos \varphi) = A \omega \end{matrix}\) .

Решая эти уравнения, найдем

\(~\operatorname {tg} = \frac{\omega^2_0 - \omega^2}{\beta \omega}\) , \(~x_0 = \frac{A \omega}{\sqrt{(\omega^2_0 - \omega^2)^2 + (\beta \omega)^2}}\) .

Видно, что теперь амплитуда отклонения шарика не обращается в бесконечность ни при каких значениях ω (см. рис.3; штриховая кривая). Но она достигает максимального значения при ω = ω₀, и это значение равно

\(~x_{0max} = \frac{A}{\beta} = \frac{qbB_0}{4 \gamma a}\) .

Результат оказался не зависящим от массы шарика.

Теперь пора приступать к измерениям. Студент выбрал шарик радиусом а = 1 мм. Но какой наибольший заряд можно сообщить этому шарику? Ясно, что такой, чтобы напряженность электрического поля у его поверхности не превышала предельно допустимого для воздуха значения E_max = 3·10⁶ В/м. Отсюда

\(~q_{max} = 4 \pi \varepsilon_0 a^2 E_{max} = \frac{10^{-6} \cdot 3 \cdot 10^6}{9 \cdot 10^9}\) Кл = 10^-9/3 Кл.

Далее, внутренний радиус соленоида был равен b = 0,1 м, а наибольшая амплитуда отклонения шарика от положения равновесия (в резонансе) оказалась равной x_0max = 0,01 мм, откуда уже легко получилось

\(~B_0 = \frac{4 \gamma a x_{0max}}{bq_{max}} = \frac{4 \cdot \frac{10^{-3}}{3} \cdot 10^{-3} \cdot 10^{-5}}{0,1 \cdot \frac{10^{-9}}{3}}\) Тл = 0,4 Тл.

Не мало, — подумал Студент. — Но неужели так же труден путь всех великих физиков?