Kvant. Закон Бернулли

Асламазов Л.Г. Закон Бернулли //Квант. — 1984. — № 5. — С. 33-34.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

В учебнике «Физика 8» рассказывается о зависимости давления р жидкости от скорости υ ее движения. Выведем формулу, связывающую эти величины количественно.

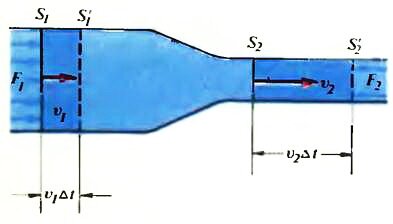
Будем считать, что труба, по которой течет жидкость, имеет широкий и узкий участки. Труба расположена горизонтально, так что потенциальная энергия жидкости в поле тяжести при течении не меняется. Выделим объем жидкости, ограниченный сечениями S₁ и S₂, где скорость жидкости равна υ₁ и υ₂ соответственно (см. рисунок). Этот объем при течении жидкости перемещается вправо. Через промежуток времени Δt он займет положение между сечениями S’₁ и S’₂, показанными на рисунке штриховыми линиями.

Так как жидкость несжимаема, уменьшение объема жидкости в широком участке трубы равно его приращению в узком участке:

\(~S_1 \upsilon_1 \Delta t = S_2 \upsilon_2 \Delta t\) или \(~S_1 \upsilon_1 = S_2 \upsilon_2\) .

Но что значит — жидкость несжимаема? Когда так говорят, имеют в виду только то обстоятельство, что изменения объема жидкости относительно малы. Небольшие деформации жидкости имеются всегда, и именно они приводят к возникновению сил давления — упругих сил сжатия жидкости.

На выделенный объем жидкости действуют силы давления с двух сторон - со стороны жидкости, следующей за ним, и со стороны жидкости, находящейся впереди. При перемещении этого объема силы давления совершают работу. Согласно теореме о кинетической энергии, полная работа сил давления равна изменению кинетической энергии жидкости:

\(~A = E_{k2} - E_{k2}\) .

Подсчитаем работу А сил давления. В сечении S₁ давление жидкости равно p₁, и сила давления F₁ = p₁S₁. За время Δt это сечение перемещается вправо на расстояние υ₁Δt, и, следовательно, сила \(~\vec F_1\) направленная вдоль перемещения, совершает работу

\(~A_1 = F_1 \upsilon_1 \Delta t = p_1 S_1 \upsilon_1 \Delta t\) .

В сечении S₂ действует сила давления \(~\vec F_2\) (F₂ = p₂S₂), направленная противоположно перемещению. Работа этой силы отрицательна:

\(~A_2 = -F_2 \upsilon_2 \Delta t = -p_2 S_2 \upsilon_2 \Delta t\) .

Полная работа сил давления

\(~A = A_1 + A_2 = (p_1 S_1 \upsilon_1 - p_2 S_2 \upsilon_2) \Delta t\) .

Вот эта работа и равна увеличению кинетической энергии жидкости.

Теперь найдем разность кинетических энергий выделенного объема жидкости до и после перемещения. Очевидно, что энергия жидкости между сечениями S’₁ и S₂ не изменяется. Поэтому общее изменение энергии будет таким, как если бы часть жидкости, заключенная между сечениями S₁ и S’₁, заняла место жидкости, заключенной между сечениями S’₂ и S’₂.

Кинетическая энергия массы жидкости m₁, протекающей за время Δt через сечение S₁ (то есть жидкости в объеме между сечениями S₁ и S’₁), равна

\(~E_{k1} = \frac{m_1 \upsilon^2_1}{2} = \rho \upsilon_1 \Delta t \cdot S_1 \frac{\upsilon^2_1}{2}\) .

где (ρ — плотность жидкости. Для сечения S₂ кинетическая энергия соответственно равна

\(~E_{k2} = \rho \upsilon_2 \Delta t \cdot S_2 \frac{\upsilon^2_2}{2}\) .

Следовательно, за время Δt кинетическая энергия выделенного объема жидкости изменилась на величину

\(~E_{k2} - E_{k1} = \left(\rho \upsilon_2 S_2 \frac{\upsilon^2_2}{2} - \rho \upsilon_1 S_1 \frac{\upsilon^2_1}{2}\right) \Delta t\) .

Приравняем эту разность работе А:

\(~\rho \upsilon_2 S_2 \frac{\upsilon^2_2}{2} - \rho \upsilon_1 S_1 \frac{\upsilon^2_1}{2} = p_1 S_1 \upsilon_1 - p_2 S_2 \upsilon_2\) .

Так как произведение площади сечения на скорость в любом сечении трубы одно и то же, написанное равенство можно сократить на величину S₁υ₁ = S₂υ₂. В результате получаем

\(~p_1 - p_2 = \frac{\rho \upsilon^2_2}{2} - \frac{\rho \upsilon^2_1}{2}\) .

Перенесем члены, относящиеся к сечению S₁, в одну сторону, а к сечению S₂ — в другую:

\(~p_1 + \frac{\rho \upsilon^2_1}{2} = p_2 + \frac{\rho \upsilon^2_2}{2}\) .

Это равенство и выражает связь между давлением и скоростью жидкости. Оно называется законом Бернулли. Согласно этому закону, там, где скорость течения жидкости больше, давление меньше и наоборот. Заметим, что величина \(~\frac{\rho \upsilon^2}{2}\) — это кинетическая энергия единицы объема жидкости. Таким образом, в любом месте трубы сумма давления и кинетической энергии единицы объема жидкости одна и та же.