Kvant. Закон Архимеда
Чивилев В.И. Закон Архимеда //Квант. — 1987. — № 1. — С. 29-30.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
«...Удар сжатого воздуха хлопнул в трубах, вода в цистерне зажурчала, и глубомер пополз вверх. Лодка всплыла на ровном киле, и глубомер показал, что рубка уже вышла из воды»,— так описывается всплытие подводной лодки в книге Л. Соболева «Морская душа».
Причина всплытия — сила Архимеда, называемая еще выталкивающей силой, которая после продувки цистерн с водой сжатым воздухом превысила по модулю силу тяжести лодки. Когда же и в каком случае возникает сила Архимеда? Со стороны чего она действует? Куда приложена, как направлена и чему равна?
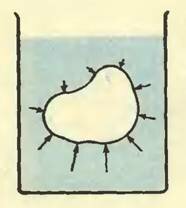
Выталкивающая сила — это сумма всех сил давления, действующих со стороны жидкости или газа на поверхность погруженного в нее тела (рис. 1). Истинная причина появления выталкивающей силы — наличие различного гидростатического давления на разных уровнях жидкости.
Для нахождения силы Архимеда мысленно заменим погруженное тело жидкостью в объеме этого тела (рис. 2).
На нее со стороны окружающей жидкости будет действовать такая же выталкивающая сила, как и на погруженное тело. По третьему закону Ньютона выделенная в объеме тела жидкость (вытесненная жидкость) будет действовать на окружающую жидкость с той же самой по модулю, но противоположно направленной силой. Это — вес вытесненного объема жидкости. Вспомним, что весом тела, неподвижного в некоторой системе отсчета (необязательно инерциальной), называется сила, с которой тело вследствие его притяжения к Земле действует на подставку или подвес. В нашем случае роль подставки для выделенного объема жидкости играет окружающая жидкость.
Итак, выталкивающая сила, действующая на погруженное в жидкость тело, равна по модулю и противоположна по направлению весу вытесненной жидкости. Это и есть закон Архимеда. Заметим, что в формулировке закона говорится именно о весе вытесненной жидкости, а не о силе тяжести. И это весьма существенно, так как вес тела (по модулю) не всегда совпадает с силой тяжести. Например, ящик массой m в кабине поднимающегося с ускорением а лифта давит на пол с силой m(g + a). Это значит, что вес ящика равен Р = m(g + a), в то время как сила тяжести, действующая на ящик, равна mg. Когда же кабина лифта опускается с тем же ускорением, вес ящика оказывается равным Р = m(g - a).
Из последнего выражения ясно, что выталкивающая сила появляется тогда, когда нет состояния невесомости, то есть любое тело (в том числе и жидкость) имеет вес. Если сосуд с жидкостью свободно падает, то жидкость находится в состоянии невесомости и на погруженное в нее тело сила Архимеда не действует. Не действует эта сила и в космическом корабле, движущемся с выключенными двигателями.
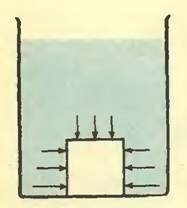
При доказательстве закона Архимеда мы считали, что тело полностью погружено в жидкость и вся его поверхность соприкасается с жидкостью. Если же часть поверхности тела плотно прилегает к стенке или дну сосуда, так, что между ними нет прослойки жидкости, то закон Архимеда неприменим. Яркой иллюстрацией сказанного служит опыт, когда ровную нижнюю поверхность деревянного кубика натирают парафином и плотно приставляют ко дну сосуда. Затем осторожно наливают воду. Брусок не всплывает, так как со стороны воды на него действует сила, не выталкивающая его вверх, а прижимающая ко дну (рис. 3).
Приведенная формулировка закона Архимеда остается справедливой и в случае, когда тело лишь частично опущено в жидкость, но не соприкасается со стенками сосуда. (Доказательство аналогично случаю полностью погруженного в жидкость тела.)
Нам осталось научиться находить вес вытесненной жидкости и линию действия выталкивающей силы. В общем случае (например, когда тело погружено в жидкость, вращающуюся вместе с сосудом) это не так легко сделать.
Рассмотрим наиболее простой и часто встречающийся на практике случай. Пусть сосуд с жидкостью неподвижен в некоторой инерциальной системе отсчета. Тогда, как известно, вес любого неподвижного тела равен силе тяжести, действующей на тело. Поэтому и выталкивающая сила равна по модулю силе тяжести, действующей на вытесненную жидкость, и противоположно ей направлена. Линия действия выталкивающей силы будет проходить через центр тяжести вытесненного объема жидкости. Покажем это.
На вытесненный объем жидкости массой m (рис. 4) действуют две силы — сила тяжести \(~m \vec g\), приложенная в центре тяжести этого объема, и выталкивающая сила \(~\vec F_B\). Так как жидкость находится в равновесии, то по правилу рычага (см. § 62 «Физики 6-7» или § 47 «Физики 8») действующие на нее силы обратно пропорциональны плечам этих сил. Плечо силы тяжести относительно оси, проходящей через центр тяжести, равно нулю. Значит, и плечо выталкивающей силы тоже равно нулю, т. е. линия действия выталкивающей силы проходит через центр тяжести «вытесненного» объема жидкости.
Поскольку точку приложения силы можно переносить вдоль линии ее действия, обычно выталкивающую силу помещают в центр тяжести вытесненной жидкости и называют эту точку также центром давлений.