Kvant. Законы сохранения

Мякишев Г.Я. Законы сохранения и системы отсчета //Квант. — 1987. — № 5. — С. 37-39.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Есть надежный способ проверить, хорошо ли вы понимаете законы, относящиеся к движению тел,— рассмотрите явление в различных инерциальных системах отсчета. Нередко сразу же обнаруживаются парадоксы, свидетельствующие о том, что настоящего понимания у вас еще нет. Часто это связано с тем, что учителя и авторы учебников и задачников заботливо выбирают систему отсчета, где процесс выглядит наиболее просто. Такая методика в значительной мере оправданна: зачем вдаваться в сложные объяснения, если можно сделать проще. Однако все это хорошо до поры до времени. В нестандартной ситуации без обстоятельного анализа и настоящего понимания не обойтись.

Все сказанное непосредственно относится, прежде всего, к закону сохранения энергии.

Потенциальная энергия и работа

Вот простейшая задача. К стене прикреплена растянутая пружина с шаром на свободном конце. Сжимаясь, пружина совершает работу, равную изменению потенциальной энергии, взятому со знаком минус:

\(~A = -\Delta E_p = \frac{kx^2}{2}\) (*)

(k — жесткость пружины, x — начальное растяжение).

Работа — произведение модулей векторов силы и перемещения на косинус угла между этими векторами — зависит от системы отсчета, так как при неизменной силе перемещение тела в различных системах отсчета различно. В то же время потенциальная энергия (а значит, и ее изменение) — функция расстояния между телами или их частями — от системы отсчета зависеть не может.

Что будет с равенством (*), если перейти в движущуюся систему отсчета? Работа изменится, а потенциальная энергия нет?

Недоразумение разрешается очень просто. В действительности изменение потенциальной энергии двух взаимодействующих тел во всех случаях равно, со знаком минус, работе двух консервативных сил, приложенных к телам. В этом все дело. Потенциальная энергия, как и сила, характеризует взаимодействие двух тел. К одному телу понятие потенциальной энергии не применимо. Обычно «для простоты» рассматриваются такие системы отсчета, в которых одно из тел (стена в нашем примере) неподвижно и поэтому одна из работ равна нулю. Работа же двух сил взаимодействия одинакова во всех системах отсчета благодаря третьему закону Ньютона. Покажем это.

Пусть два тела взаимодействуют друг с другом и в неподвижной системе отсчета совершают перемещения \(~\vec s_1\) и \(~\vec s_2\), совпадающие по направлен нию с соответствующими силами \(~\vec F_1\) и \(~\vec F_2\), причем \(~\vec F_1 = -\vec F_2\), F₁ = F₂ (рис. 1, а). Тогда полная работа

\(~A = A_1 + A_2 = F_1 s_1 + F_2 s_2\) .

Рис. 1

При переходе в систему отсчета, движущуюся относительной первой, оба тела получают дополнительные перемещения \(~\vec s_0\) (рис. 1, б). Работа в этой системе

\(~A' = A'_1 + A'_2 = F_1 (s_1 + s_0) + F_2 (s_2 - s_0) = (F_1 s_1 + F_2 s_2) + (F_1 s_0 - F_2 s_0) = A\) .

Заметим, что полученный результат справедлив не только для консервативных сил — тяготения и упругости, но и для сил трения.

Работа сил трения

Говорят, и правильно говорят, что работа внутренних сил трения в системе всегда отрицательна. Как это доказать?

Нельзя ведь утверждать, что сила трения во всех случаях совершает отрицательную работу. Положите ручку на лист бумаги и потяните за лист. Сила, приложенная со стороны ручки к листу, совершает отрицательную работу, но сила, приложенная к ручке,— положительную. Кроме того, выбором системы отсчета работу любой силы из отрицательной можно превратить в положительную за счет изменения направления перемещения.

Однако в системе отсчета, где одно из взаимодействующих тел неподвижно, работа всегда отрицательна, так как сила трения направлена против скорости относительного движения тел. Только что было показано, что работа двух сил взаимодействия от системы отсчета не зависит. Поэтому и в любой системе отсчета суммарная работа сил трения отрицательна.

Кинетическая энергия и работа

С кинетической энергией в различных системах отсчета дело обстоит совсем иначе, чем с потенциальной. Кинетическая энергия относится к одному телу, а не к двум. Изменение кинетической энергии тела равно работе одной равнодействующей силы, т. е. сумме всех сил, приложенных к данному телу. Эти силы могут быть как внутренними силами системы, так и внешними.

Согласно теореме о кинетической энергии,

\(~\Delta E_k = A\) .

При переходе в другую систему отсчета, движущуюся со скоростью \(~\vec \upsilon_0\) относительно первой (рис. 2), кинетическая энергия изменяется:

\(~E_k = \frac{m \upsilon^2_1}{2}\) , \(~E'_k = \frac{m \upsilon^2_2}{2} = \frac{m (\upsilon_1 - \upsilon_0)^2}{2} = \frac{m \upsilon^2_1}{2} - m (\upsilon_1 \upsilon_0) + \frac{m \upsilon^2_2}{2}\) ,

где υ₁ — скорость тела в первой системе отсчета, а υ₂ = υ₁ - υ₀ — во второй. При действии на тело внешней силы, по теореме о кинетической энергии, в движущейся системе отсчета

\(~\Delta E'_k = A'\) .

Рис. 2

Таким образом, при переходе от одной системы отсчета к другой меняется не только кинетическая энергия, но и изменение кинетической энергии. Но всегда изменение кинетической энергии равно работе сил в этой же системе отсчета.

Определить, как меняется кинетическая энергия в зависимости от системы отсчета, не сложно, Вычислить же изменение работы гораздо сложнее. Рассмотрим такую задачу.

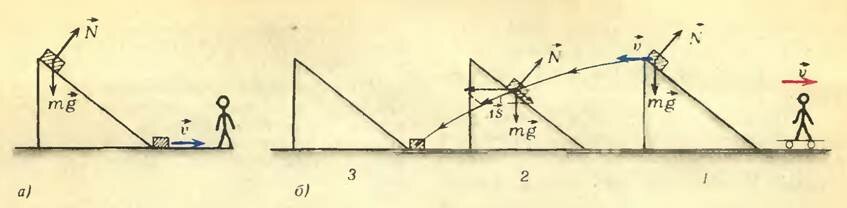
Кубик соскальзывает без трения с наклонной плоскости высотой h (рис. 3, а). У основания плоскости кинетическая энергия \(~E_{k2} = \frac{m \upsilon^2}{2}\), а начальная энергия E_k1 = 0. Изменение кинетической энергии равно работе силы тяжести:

\(~\Delta E_k = E_{k2} - E_{k1} = \frac{m \upsilon^2}{2} = mgh\) .

Рис. 3

Рассмотрим движение кубика с точки зрения инерциальной системы отсчета, движущейся относительно наклонной плоскости со скоростью \(~\upsilon = \sqrt{2gh}\) (рис. 3, б). В этой системе начальная скорость кубика равна \(~\upsilon = \sqrt{2gh}\), а конечная скорость равна нулю, поэтому

\(~\Delta E'_k = E'_{k2} - E'_{k1} = -\frac{m \upsilon^2}{2} \ne mgh\) .

Согласно теореме о кинетической энергии,

\(~\Delta E'_k = -mgh = A'\)

— работа оказывается отрицательной. Дело в том, что в движущейся системе отсчета сила реакции плоскости не перпендикулярна перемещению кубика. Она-то и совершает отрицательную работу (наряду с положительной работой силы тяжести), уменьшающую кинетическую энергию кубика. Однако вычислить ее непосредственно, не прибегая к закону сохранения энергии, весьма затруднительно.

Закон сохранения импульса

Импульс силы не зависит от системы отсчета. Поэтому и изменение импульса тела одинаково во всех инерциальных системах отсчета:

\(~\Delta \vec P = \vec F \Delta t\) .

В данном случае все очень просто — импульс тела при переходе от одной системы отсчета к другой меняется, но изменение импульса остается одним и тем же.