Kvant. Если исчезнет трение

Агаян В., Хазен И. Что произойдет, если исчезнет трение? //Квант. — 1990. — № 5. — С. 50-53.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Как показывают оценки, на преодоление трения и его разрушительных последствий человечество тратит примерно 5—10 % всей совершаемой им работы. Если же трение исчезнет, то в машинах, станках, двигателях и других различных устройствах, участвующих в современных производственных процессах, уменьшатся потери энергии, износ, шум.

Но, вместе с тем, если исчезнет трение, то.... наступит хаос. Движущиеся поезда, автомобили, велосипеды, трамваи не смогут остановиться, а покоящиеся — не смогут тронуться с места. Беспомощно будут барахтаться пешеходы, сползая вместе с припаркованными автомобилями и другими предметами по уклонам улиц. Развяжутся узлы на всех нитках и веревках. Сами собой начнут раскручиваться гайки и выпадать шурупы. Обвиснут струны роялей, гитар. Смычки перестанут извлекать звуки из скрипок, альтов, виолончелей...

Но может ли исчезнуть трение? Что значит «трение отсутствует»? Что такое, наконец, сила трения? Об этом и пойдет речь в заметке.

Как известно, сила трения (точнее — сила сухого трения) F определяется коэффициентом трения k, зависящим от рода веществ, из которых сделаны трущиеся тела, и качества обработки их поверхностей, и силой N нормального давления одного тела на другое:

\(~F = kN\) .

Представим себе, что у всех окружающих нас тел любой малый участок поверхности абсолютно гладкий, т. е. k_i = 0. Тогда при любой величине силы N_i, действующей на этот участок, N_i = 0. Очевидно, что это и означало бы, что трение как свойство вещества исчезло.

Однако оказывается, что даже если трение как свойство вещества исчезнет, сила трения между телами, тем не менее, может проявляться. Для того чтобы это пояснить, рассмотрим пример.

Рис. 1

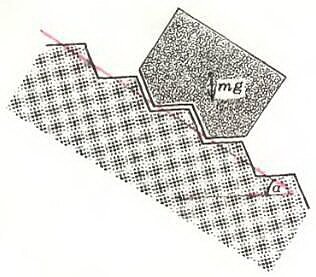
Изготовим из вещества, не обладающего трением, два тела, у которых соприкасающиеся поверхности имеют одинаковые бороздки с сечением в виде равнобедренных треугольников с углом при основании α, длиной основания 2l и высотой h (рис. 1). Пусть масса верхнего тела равна m и, соответственно, сила нормального давления верхнего тела на нижнее равна N = mg. Приложим к верхнему телу вдоль горизонтальной плоскости, «осредняющей» бороздки, силу F и будем пытаться с помощью этой силы медленно сдвинуть верхнее тело относительно нижнего. Понятно, что когда верхнее тело переместится по горизонтали на величину l, его центр тяжести поднимется на высоту h и тело приобретет потенциальную энергию

\(~E_p = mgh\) .

При этом сила F совершит работу

\(~A = Fl\) .

Согласно закону сохранения механической энергии,

\(~E_p = A\), или \(~mgh = Fl\) ,

откуда

\(~F = \frac hl mg\) .

Обозначим отношение \(~\frac hl\) через k, учтем, что mg = N, и получим

\(~F = kN\) .

Отсюда видно, что для того чтобы в условиях отсутствия трения одно тело начало движение по поверхности другого, надо приложить силу, величина которой определяется точно так же, как и величина силы трения.

Таким образом, предположение о том, что трение как свойство вещества исчезло, не привело к исчезновению силы трения. При этом коэффициент трения оказывается зависящим только от геометрических параметров неровностей на поверхности соприкасающихся тел.

Рис. 2

Безусловно, всем хорошо известна задача, в которой смысл коэффициента трения иллюстрируется с помощью наклонной плоскости и находящегося на ней тела. Если менять угол наклона плоскости к горизонту, начиная от нуля, то коэффициент трения будет равен тангенсу такого угла α₀, при котором лежащее на плоскости тело начнет соскальзывать. Но и в рассмотренном нами идеализированном примере отсутствия трения как свойства вещества движение тела на наклонной плоскости начинается с углов α₀, для которых \(~\operatorname{tg} \alpha_0 = \frac hl\) (рис. 2). Значит, опять коэффициент трения равен тангенсу угла наклона поверхности контакта тел, при котором одно тело начинает движение по поверхности другого.

Вернемся, однако, к нашему первому примеру (см. рис. 1). В действительности сила трения существует не только в начале движения, поэтому рассмотрим, что будет происходить с нашими идеальными телами, когда их взаимное перемещение по горизонтали станет больше l. Верхнее тело, поднявшись на гребень бороздки, начнет опускаться вниз, его потенциальная энергия будет переходить в кинетическую, а в конце спуска произойдет удар о восходящую грань следующей бороздки. Если при этом опять окажется возможным полное преобразование кинетической энергии в потенциальную, т. е. будет возможен подъем верхнего тела на гребень следующей бороздки, то дальнейшее движение верхнего тела сможет осуществляться без приложения дополнительной силы. А это и будет означать, что сила трения исчезла. Если же этого не произойдет, то, несмотря на полное отсутствие трения как свойства вещества, сила трения сохранится.

Рис. 3

Рассмотрим подробнее изменение скорости верхнего тела при ударе о грань следующей бороздки (рис. 3). Будем считать, что условия идеальные и при ударе нет потерь энергии (т. е. происходит абсолютно упругий удар). В таком случае справедлив известный закон: угол падения равен углу отражения; при этом углы отсчитываются от перпендикуляра к поверхности, с которой происходит соударение, т. е. от перпендикуляра к восходящей грани бороздки в нашем случае (см. углы γ на рисунке 3).

Обозначим скорость в конце спуска через \(~\vec \upsilon_1\) (она направлена вдоль плоскости спуска с бороздки), а скорость после удара — через \(~\vec \upsilon_2\). Разложим эти скорости на составляющие вдоль осей X и Y, направленных по горизонтали и по вертикали соответственно):

\(~\begin{matrix} \upsilon_{1x} = \upsilon_1 \cos \alpha, \upsilon_{1y} = \upsilon_1 \sin \alpha \\ \upsilon_{2x} = \upsilon_2 \cos \varphi, \upsilon_{2y} = \upsilon_2 \sin \varphi \end{matrix}\) .

Из рисунка 3 найдем соотношение между углами α и φ:

\(~\begin{matrix} \varphi = \pi - \alpha - 2\gamma \\ \gamma = \pi - \frac{\pi}{2} - 2\alpha = \frac{\pi}{2} - 2\alpha \end{matrix}\) ,

откуда

\(~\varphi = 3 \alpha\) .

Воспользуемся известными из справочников формулами тригонометрии

\(~\begin{matrix} \cos 3 \alpha = 4 \cos^3 \alpha - 3 \cos \alpha \\ \sin 3 \alpha = -4 \sin^3 \alpha + 3 \sin \alpha \\ \cos^2 \alpha + \sin^2 \alpha = 1 \end{matrix}\)

и запишем отношения соответствующих проекций скоростей после удара и до него:

\(~\begin{matrix} \frac{\upsilon_{2x}}{\upsilon_{1x}} = \frac{\cos 3 \alpha}{\cos \alpha} = 1 - 4 \sin^2 \alpha \\ \frac{\upsilon_{2y}}{\upsilon_{1y}} = \frac{\sin 3 \alpha}{\sin \alpha} = -(1 - 4 \cos^2 \alpha) \end{matrix}\) .

В условиях сохранения энергии верхнее тело после удара о нижнее поднимется в точности на гребень следующей бороздки только в том случае, если вектор скорости \(~\vec \upsilon_2\) будет направлен вверх по плоскости бороздки, а величина скорости останется такой же, как и до удара. Этому отвечает условие

\(~\frac{\upsilon_{2x}}{\upsilon_{1x}} = 1\) и \(~\frac{\upsilon_{2y}}{\upsilon_{1y}} = -1\).

Но, в силу приведенных выше формул, это возможно только при α = 0, т. е. когда поверхности соприкасающихся тел абсолютно гладкие, без всяких бороздок! Во всех остальных случаях невозможно полное преобразование кинетической энергии в потенциальную такое, чтобы затем верхнее тело могло неограниченно продолжать свое движение без приложения внешней силы. Если, например, \(~\frac{\upsilon_{2x}}{\upsilon_{1x}} = 1 - 4 \sin^2 \alpha < 0\), т. е. \(~\alpha > \frac{\pi}{6}\), то компонента υ_2x направлена навстречу движению, поэтому сила F должна не только компенсировать потери кинетической энергии при ее преобразовании в потенциальную, но и совершать работу, большую, чем в начале движения.

Из рассмотренного примера возникает парадоксальный вывод: если трение как свойство вещества и может исчезнуть, то это не приведет к исчезновению силы трения, включая и ее характерную особенность — различие в величине силы трения в начале движения и при его продолжении. Останутся также и такие сопутствующие трению явления, как шум из-за ударов неровностей друг о друга и разрушение поверхностей тел (если, например, сломать выступы бороздок окажется легче, чем подняться по ним вверх). Наконец, самое интересное следствие состоит в том, что сохраняется зависимость силы трения между телами от того, из какого вещества они изготовлены, так как при одинаковом способе механической обработки поверхностей форма неровностей для разных веществ может быть различной.