Kvant. Два торнадо

Вышинский В. Два торнадо и несколько ворон // Квант. — 2004.— № 3. — С. 30-31.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Рис 1. Вихревой след самолета и его простейшая модель

Я шел по опушке весеннего леса, прислушиваясь к крику кукушки. Низко пролетел самолет — кукушка на мгновение замолкла, но, к моей радости, тут же продолжила счет оставшихся лет. Вдруг без видимой причины зашуршали листья, и некоторые из них взметнулись вверх. Линия возмущения хлыстом пробежала по поляне, нарушая тихий покой листьев, и запуталась в ветвях деревьев. Так я впервые «увидел» вихревой след от самолета — два «горизонтальных торнадо», как окрестили американцы это грозное явление. Статистика знает множество летных происшествий и авиакатастроф, связанных с попаданием в вихревой след. Но о грустном - в другой раз.

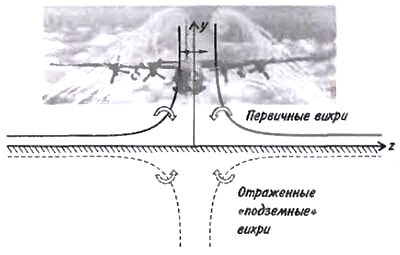
Что же произошло в лесу? Давайте построим физическую модель явления. При полете самолета в атмосфере, как следствие создания подъемной силы, возникает вихревой след (рис. 1,а). В первом приближении крыло самолета можно заменить так называемым присоединенным вихрем (рис. 1,б). Так в свое время предложил делать Л.Прандтль, один из основателей аэродинамики. Вихри имеют свойство не оканчиваться просто так - они либо уходят в бесконечность, либо замыкаются друг на друга, образуя вихревые кольца, либо опираются на твердую поверхность, как это делает смерч (торнадо). От присоединенного вихря вниз по потоку отходит пара вихревых жгутов - свободных вихрей. Получается П-образный вихрь (рис.1,в), который является первым приближением вихревой системы самолета.

Свободные вихри имеют противоположную скорость вращения и настолько свободны, что опускаются в атмосфере под действием «взаимной индукции» - скорости, создаваемой своим партнером. Вблизи земли вихри уже так «надоедают» друг другу, что разбегаются в разные стороны. Это связано с условием непротекания, которое проще всего моделируется парой зеркально отраженных «подземных» вихрей противоположного знака (рис.2). Замерив время опускания вихрей и зная тип самолета, можно оценить высоту его полета.

Рис. 2. Разбегание вихрей у земли

Об этом случае я вспомнил в аэропорту города Франкфурта-на-Майне. Там в пространстве под глиссадой - невидимой линией, по которой воздушные суда заходят на посадку, - между двумя параллельными взлетно-посадочными полосами (ВПП) расположены вышки со специальными измерительными приборами - ультразвуковыми анемометрами (рис.3). Эта система называется ветровой линией и служит для определения ветровой обстановки в зоне ВПП. На вышках восседали вороны, лениво перекаркиваясь между собой и не обращая внимания на садящиеся самолеты.

Рис. 3. Схема захода самолета на посадку

Я стал с интересом наблюдать, что же будет дальше. Вскоре довольно тихо зашел на посадку самолет фирмы «Боинг» (В-747). Он пронесся в воздухе, коснулся ВПП, деловито пробежал почти до полной остановки и свернул на рулежную дорожку. В этот момент с ближайшей к ВПП мачты ветровой линии свалилась ворона. Она, взмахнув крыльями, перевернулась в воздухе, и «кар» застрял у нее в глотке. То же самое повторилось через некоторое время (20-30 секунд) с вороной на соседней мачте. Третья ворона удержалась, но была сильно удивлена и испугана воздушным «шлепком».

Я решил подсчитать скорость разбегания вихрей. Расстояние между вышками около 50 метров, интервал между сваливанием ворон около полминуты; таким образом, скорость разбегания вихрей у земли оказалась порядка 2 м/с. Получился неплохой результат, так что по темпу «сваливания ворон» с вышек можно, в первом приближении, определить тип севшего самолета.

Действительно, пусть известен вес самолета G = mg и размах его крыла l. По теореме Жуковского, погонная подъемная сила профиля крыла (в расчете на единицу длины крыла) пропорциональна так называемой циркуляции скорости Г (см. Примечание 1), скорости полета u_∞ и плотности воздуха ρ\[~\frac{F_y}{\Delta l} = \rho u_{\infty} \Gamma\]. Тогда в предположении, что эта циркуляция распределена приблизительно постоянно по размаху крыла: Г(z) = Г₀, получим

\(~F_y = G = \rho u_{\infty} \Gamma_0 b\) ,

где u_∞ = 70 м/с при полете по глиссаде, а b - расстояние между присоединенными вихрями (см. Примечание 2). Скорость, индуцируемая соседним потенциальным вихрем в области данного вихря (см. Примечание 3), равна

\(~\upsilon_i = \frac{\Gamma_0}{2 \pi b}\) ,

так что скорость опускания вихревой пары составляет

\(~\upsilon_y = \frac{G}{2 \pi \rho u_{\infty} b^2}\) .

Разумно считать, что скорость разбегания вихрей υ_z приблизительно равна скорости опускания υ_y. Измерив υ_z по методу «сваливания ворон», можно найти отношение \(~\frac{G}{b^2}\) и по соответствующей таблице определить тип севшего самолета. Например, для самолета Ил-96 (размах крыла l = 58 м, максимальная взлетная масса m = 270 т) b = 45,5 м, \(~\frac{G}{b^2}\) ≈ 1300 н/м², а для самолета В-747 (l = 64 м, m = 370 т) b = 50 м , \(~\frac{G}{b^2}\) ≈ 1500 н/м². Более точные расчеты дают скорость опускания вихрей для последнего самолета υ_y = 2,8 м/с на режиме посадки (u_∞ = 79 м/с, Г₀ = 833 м²/с) и υ_y = 2,1 м/с на крейсерском режиме полета (u_∞ = 250 м/с , Г₀ = 605 м2²/с ). Для самолета В-757 (l = 38 м, m = 109 т) получается b ≈ 30 м, \(~\frac{G}{b^2}\) ≈ 1200 н/м². Этот самолет замечателен тем, что имеет очень большую (измеренную в летном эксперименте) максимальную касательную скорость в вихре (до 100 м/с - действительно, маленький торнадо), хотя относится к классу средних самолетов.

Вот что прошуршали мне листья в осеннем лесу и прокаркали вороны во фракнфуртском аэропорту...

Примечание 1

Циркуляция скорости Г (ее размерность [Г] = м²/с) есть мера завихренности потока. Она определяется как интеграл вдоль замкнутой кривой L от произведения проекции скорости на касательную к этой кривой υ_τ и элемента длины кривой ds:

\(~\Gamma = \oint\limits_{L} \upsilon_{\tau} ds\) .

Примечание 2

Расстояние между свободными вихрями b несколько меньше размаха крыла l. Для крыла с эллиптическим распределением циркуляции Г(z) (такое распределение в определенном смысле является оптимальным) \(~b = \frac{\pi}{4} l\).

Примечание 3

Потенциальный вихрь - это такой вихрь, у которого вся завихренность сосредоточена в центре и вокруг этого центра происходит вращение частиц газа без вращения вокруг собственной оси. На расстоянии r он индуцирует скорость

\(~\upsilon_i(r) = \frac{\Gamma_0}{2 \pi r}\) .