Kvant. Вращение
Черноуцан А.И. Когда вокруг всё вертится... //Квант. — 1992. — № 9. — С. 45-47.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Начав изучать кинематику, вы наверное заметили, какое большое внимание уделяется понятию «система отсчета» (СО). Действительно, бессмысленно говорить о движении тела или точки, если не указывать, относительно какого другого тела (тела отсчета) производятся измерения координат, скорости и ускорения. Самая привычная СО — земля, однако иногда бывает удобно перейти в СО, связанную с движущимся воздухом (ветром), водой в реке и т. д. Кроме того, изучая движение самой Земли по орбите или вокруг собственной оси, переходят в СО, связанную с Солнцем и звездами?
Переходя из одной СО в другую, не надо, конечно, пересаживаться из одного движущегося «экипажа» в другой. Зачастую это было бы просто невозможно. «Переход» производят мысленно, вычисляя, какие результаты получил бы движущийся наблюдатель при измерении координат, скорости и ускорения. Например, закон сложения скоростей позволяет связать между собой скорость тела C относительно неподвижной системы отсчета A(\(~\vec \upsilon_C\)), его скорость относительно движущейся системы B (так называемая относительная скорость \(~\vec \upsilon_{CB}\) скорость движущейся СО относительно неподвижной (\(~\vec \upsilon_B\)):
Однако простое и однозначное применение закона сложения скоростей возможно только тогда, когда одна СО движется относительно другой поступательно. Именно в этом случае все точки СО B имеют относительно A одинаковую скорость \(~\vec \upsilon_B\) и можно просто говорить о скорости одной СО относительно другой. А как быть, если одна СО совершает относительно другой не поступательное, а вращательное движение?
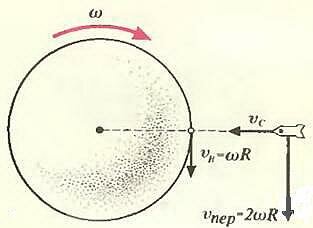
Рассмотрим пример. Предположим, что космический корабль C приближается к быстро вращающейся с угловой скоростью ω планете B со скоростью \(~\vec \upsilon_C\), находясь в ее экваториальной плоскости (рис. 1). Командир корабля дает распоряжение двум стажерам: найдите скорость \(~\vec \upsilon_{CB}\) нашего корабля с точки зрения наблюдателей на планете в тот момент, когда расстояние до поверхности планеты будет равно ее радиусу R.
Первый стажер знал кинематику весьма поверхностно. Он решил применить закон сложения скоростей. Для этого он сначала вычислил скорость наблюдателя на поверхности планеты\[~\upsilon_B = \omega R\]. Потом, считая, что наблюдатель находится в момент наблюдения точно под кораблем, нашел направление и модуль вектора \(~\vec \upsilon_{CB}\):
Второй стажер знал кинематику гораздо лучше (наверное, он выписывал журнал «Квант»). Он рассуждал следующим образом. Посмотрим, какую скорость нужно иметь на высоте R (на расстоянии 2R от центра планеты), чтобы казаться неподвижным наблюдателю на планете. Для этого представим, что планета заполняет все пространство. Тогда в данном месте воображаемые точки планеты имеют скорость \(~\upsilon_{per} = \omega \cdot 2R\) — ее называют переносной скоростью,— а скорость корабля относительно вращающейся СО равна
Именно этот стажер стал вскоре постоянным членом экипажа.
(Хотя этот пример немного шуточный, аналогичные проблемы действительно возникают при наблюдении за удаленными спутниками и ракетами с вращающейся Земли.)
Итак, общее правило состоит в том, что закон сложения скоростей можно применять и в случае вращающихся СО, но нужно брать скорость не самой СО (это понятие не имеет смысла — разные точки СО движутся по-разному), а переносную скорость — скорость той точки вращающейся СО, где в данный момент находится тело:
Это правило выглядит вполне очевидным, если вы находитесь непосредственно на вращающемся теле. Тогда переносная скорость — это скорость тела у вас под ногами (если вы остановитесь, вращающееся тело будет «переносить» вас в пространстве именно с этой скоростью).
Например, если вы идете по вращающейся с угловой скоростью ω платформе вдоль ее радиуса (рис. 2) со скоростью \(~\vec \upsilon_{otn}\),a платформа у вас под ногами имеет скорость \(~\upsilon_{per} = \omega R\), где R — изменяющееся расстояние от центра платформы, то ваша полная скорость относительно земли будет равна
Психологическая трудность, с которой столкнулся незадачливый стажер, состояла в том, что корабль находился вне вращающегося тела (планеты) и у него не хватило воображения мысленно распространить планету на окружающее пространство и правильно вычислить переносную скорость.
Чтобы проверить, все ли вы поняли, решите такую задачу.
Две одинаковые круглые платформы, на которых сидят наблюдатели Аи В, вращаются навстречу друг другу с одной и той же угловой скоростью 1 рад/с (рис. 3). Радиусы платформ 2 м, расстояние между их центрами 5 м. Чему равна скорость человека А относительно наблюдателя В в момент, указанный на рисунке 3?
Не торопитесь. Ответ — в конце статьи.
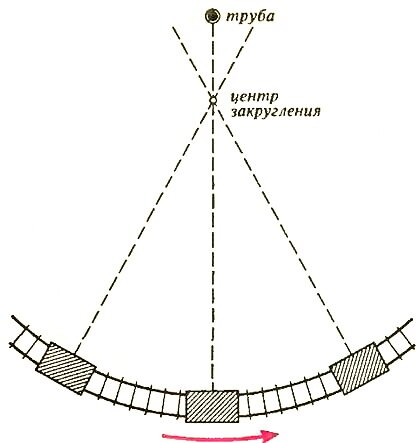
Теперь еще один (менее глобальный) пример, в котором незнание того, что выбранная СО поворачивается, может привести к неожиданному эффекту. Предположим, что.сидя у окна в купе скорого поезда, вы рассеянно любуетесь пейзажем. Бегут назад деревья, дома... И вдруг вы замечаете, что расположенная вдалеке фабричная труба движется не назад, а вперед, обгоняя поезд! В чем тут дело? Объяснение очень простое — вы не заметили, что поезд начал поворачивать по дуге большого радиуса, и теперь вы находитесь во вращающейся СО, хотя сами этом не знаете. Посмотрите на рисунок 4. Если бы труба находилась в центре закругления, она казалась бы вам неподвижной, потому что переносная скорость в этой точке равна нулю и скорость трубы относительно земли тоже равна нулю. А если труба окажется дальше, чем центр окружности, то переносная скорость в этом месте будет направлена назад, а относительная — вперед, и будет казаться, что труба обгоняет поезд.
Возможно, у вас возник вопрос — а имеем ли мы право переходить во вращающиеся СО? Может быть, это незаконно, и мы можем пользоваться только такими СО, которые движутся равномерно и поступательно? Ведь нелепо утверждать, что между ними нет разницы. Попробуй усидеть на быстро вращающейся карусели — тебя так и норовит выкинуть наружу. А вот в быстро летящем самолете чувствуешь себя вполне комфортно (кроме взлета и посадки).
В некотором смысле вы правы. С точки зрения динамики, есть выделенные СО — так называемые инерциальные, в которых действуют законы Ньютона, а все СО, движущиеся относительно них с ускорением (в том числе и вращающиеся), являются неинерциальными. Например, СО, связанную с Солнцем и звездами, можно считать инерциальной, а СО, связанную с Землей или с ускоряющейся ракетой,— нет. Однако эта разница важна только с точки зрения динамики. В рамках кинематики, если не думать о том, почему тела так движутся, а заниматься только описанием их движения, все СО являются законными и равноправными.
А теперь — обещанный ответ к задаче: относительная скорость равна 1 м/с.