Kvant. Аэродинамический парадокс

Митрофанов А. Аэродинамический парадокс спутника //Квант. — 1998. — № 3. — С. 2-6.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Неожиданное случается в жизни чаще, чем ожидаемое.
Тит Макций Плавт
Парадоксы — вот единственная правда.
Бернард Шоу

Попробуем ответить на вопрос, может ли тело, двигаясь в среде и испытывая действие силы со стороны среды, увеличить свою скорость. На первый взгляд, такое событие кажется не более правдоподобным, чем известное предложение барона Мюнхгаузена тащить себя за волосы. Казалось бы, скорость тела в среде должна только уменьшаться, однако не торопитесь с выводами. Такие случаи вполне возможны и в той или иной степени наблюдаются при движении искусственных спутников и метеоритов вокруг планет в разреженной атмосфере. Речь идет об известном аэродинамическом парадоксе спутника — попадая в верхние слои атмосферы, космический аппарат, испытывая торможение в разреженном газе, увеличивает при этом скорость своего движения.

Прежде чем перейти к описанию происходящего на орбите, рассмотрим более простой пример из механики. Пусть небольшое тело закреплено на конце растяжимой упругой нити, пружины, резинового шнура или какого-то другого подвеса и движется с постоянной скоростью в плоскости по окружности. Будем считать, что для подвеса справедлив закон Гука, т.е. сила натяжения пропорциональна удлинению подвеса. Оказывается, если тело каким-либо образом начать тормозить, его движение изменится. В частности, если тело мгновенно остановить, а потом отпустить, то растянутый подвес сообщит телу некоторую скорость в направлении прежнего центра вращения. Максимальную скорость, которую приобретет тело, можно найти из закона сохранения энергии для системы тело — упругий подвес. В случае, когда растяжение подвеса значительно превышает его начальную длину, максимальная конечная скорость тела будет почти равна начальной скорости вращения по окружности.

Наш пример - упрощенная аналогия задачи о торможении спутника в атмосфере: тело — это спутник, а упругий подвес — модель притяжения Земли. Конечно, эта аналогия грубая, так как закон Гука вовсе не описывает гравитационные силы, которые (как и кулоновские силы, действующие между зарядами) обратно пропорциональны квадрату расстояния между телами, а в нашем случае — квадрату радиуса орбиты. Движение спутника в верхних слоях атмосферы планеты происходит сложней и интересней, чем движение шарика на резиновом подвесе.

Для изучения эволюции орбиты спутника, двигающегося в разреженном газе, нам потребуются некоторые формулы. Рассмотрим движение спутника массой m по круговой орбите радиусом R вокруг Земли, масса которой М. Для высоких орбит, когда притяжение Земли является основной силой, оказывающей влияние на движение спутника, его скорость определяется уравнением

\(~\upsilon^2 = \frac{GM}{R^2},\) или \(~\upsilon = \upsilon_0 \sqrt{\frac{R_0}{R}}, \qquad (1)\)

где G — гравитационная постоянная, R₀ — радиус Земли, равный примерно 6400 км, а \(~\upsilon_0 = \sqrt{g_0 R_0}\) — первая космическая скорость спутника, равная 7,9 км/с для нашей планеты (g₀ = 9,8 м/с² — ускорение свободного падения вблизи поверхности Земли).

Сила сопротивления, действующая со стороны разреженного газа на спутник в верхних слоях атмосферы, определяется формулой

\(~F_{sopr} = C_x \frac{\rho \upsilon^2}{2} S_x. \qquad (2)\)

Здесь ρ — плотность атмосферы на орбите, которая сильно зависит от высоты полета спутника; S_x — площадь поперечного сечения спутника, точнее — площадь максимального сечения спутника плоскостью, перпендикулярной вектору скорости \(~\vec \upsilon\) полета спутника относительно среды (или, как говорят, площадь миделя); C_x — так называемый коэффициент лобового сопротивления, зависящий, вообще говоря, от скорости, но для реальных условий полета спутника на большой высоте его можно считать примерно равным 2. Последнее просто означает, что соударения молекул и атомов с обшивкой спутника неупругие, в результате чего спутнику в единицу времени передается импульс, равный ρυ² на единицу площади поперечного сечения. Напомним, что орбитальная скорость спутника во много раз превышает среднюю тепловую скорость молекул и атомов атмосферного газа. (Если бы было иначе, то, как нетрудно догадаться, Земля очень быстро потеряла бы свою атмосферу!) Поэтому собственное движение частиц среды в рассматриваемых примерах при расчетах сил торможения можно не учитывать.

К каким же следствиям приводит наличие разреженного газа (или, как говорят, атмосферного «хвоста») на орбите спутника? Для высоких орбит учет силы сопротивления среды можно рассматривать как малые возмущения, приводящие к небольшим изменениям параметров орбиты. Плавно тормозясь в разреженном газе, спутник переходит на более низкую орбиту. Но при меньших R, как следует из формулы (1), скорость орбитального движения спутника должна быть больше, чем на первоначальной более высокой орбите. Получается, что сила сопротивления, направленная против движения, может ускорить спутник в направлении этого же движения! Более того, оказывается (как мы увидим дальше из расчетов), что тангенциальное ускорение, т.е. ускорение вдоль траектории, точно равно силе сопротивления, деленной на массу спутника. Этот интересный факт и называется аэродинамическим парадоксом спутника, к объяснению которого мы сейчас перейдем.

Заметим, что с этой, казалось бы, непростой задачей можно справиться, используя только законы сохранения и проводя элементарные вычисления.

Увеличение скорости спутника при его торможении в верхних слоях атмосферы имеет простую причину. Спутник, теряя первоначальную круговую скорость, попросту говоря, падает в гравитационном поле Земли, приближаясь к ней, так как сила притяжения \(~F = G \frac{mM}{R^2}\) становится больше силы \(~\frac{m \upsilon^2}{R}\), необходимой для того, чтобы удержать спутник на прежней орбите. Но падает космический аппарат не отвесно (как кирпич с крыши высокого дома), а по плавной кривой — спирали, виток за витком медленно приближаясь к земной поверхности, причем каждый виток спирали мало отличается от окружности. А в поле тяжести, как мы знаем, при падении тел их скорость увеличивается. Для такого движения космического аппарата уменьшение его потенциальной энергии не только компенсирует работу сил трения на орбите, т.е. сил сопротивления среды, но и служит причиной увеличения его скорости υ и кинетической энергии \(~\frac{m \upsilon^2}{2}\). Так что ускоряет падающий спутник земное притяжение, а вовсе не силы трения спутника на орбите. Последние лишь помогают «сбросить» космический аппарат с более высокой орбиты на более низкую. (Вспомните простенький пример с шариком на упругом подвесе, о котором шла речь в начале статьи.)

Рис. 1

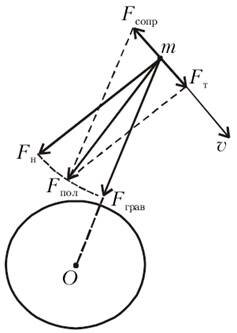
Обратимся к рисунку 1, где показаны траектория искусственного спутника в разреженной атмосфере и силы, действующие на него. Движение происходит в плоскости при медленном уменьшении радиуса орбиты, т.е. по плавно закручивающейся к Земле спирали с малым шагом по сравнению с высотой полета спутника h = R - R₀. Здесь \(~\vec F_{grav}\) — сила гравитационного притяжения спутника к Земле, \(~\vec F_{sopr}\) — сила сопротивления со стороны атмосферы и \(~\vec F_{pol}\) — векторная сумма сил \(~\vec F_{grav}\) и \(~\vec F_{sopr}\). Поскольку траекторией движения является спираль, каждый виток которой хотя и мало, но все же отличается от окружности, силу \(~\vec F_{pol}\) можно разложить на две составляющие\[~\vec F_n\] и \(~\vec F_t\), т.е. нормальную и тангенциальную (касательную) к траектории космического аппарата. Сила \(~\vec F_t\), действующая вдоль траектории спутника, увеличивает его скорость таким образом, что в данной точке траектории мгновенное ускорение в направлении вектора \(~\vec \upsilon\) равно по модулю \(~\frac{F_t}{m}\). Покажем, что F_t = F_sopr.

Пусть на некоторой орбите радиусом R на спутник действует сила торможения F_sopr, определяемая формулой (2), в которой плотность ρ(R) на всем витке считается малой и постоянной величиной. Определим увеличение скорости спутника Δυ и уменьшение радиуса его орбиты ΔR на одном витке полета. Воспользуемся законом сохранения энергии с учетом работы силы сопротивления. Напомним, что потенциальная энергия спутника на орбите равна \(~W_1 = - G \frac{mM}{R} = -m \upsilon^2\), кинетическая энергия равна \(~W_2 = \frac{m \upsilon^2}{2} = - \frac{W_1}{2}\), а полная энергия составляет \(~W_1 + W_2 = -\frac{m \upsilon^2}{2}\). Запишем баланс полной энергии спутника в начале и в конце витка:

\(~-\frac{m \upsilon^2}{2} - 2 \pi RF_{sopr} = -\frac{m (\upsilon + \Delta \upsilon)^2}{2}. \qquad (3)\)

Откуда, с учетом условия \(~\Delta \upsilon \ll \upsilon\) следует

\(~\Delta \upsilon = \frac{2\pi F_{sopr} R}{m \upsilon} = \frac{2\pi F_{sopr} \sqrt R}{m \sqrt g},\)

или

\(~\frac{\Delta \upsilon}{\upsilon} = \frac{2\pi F_{sopr}}{mg}. \qquad (4)\)

Поскольку продолжительность витка составляет \(~\Delta t = \frac{2 \pi R}{\upsilon}\), тангенциальное ускорение пролетающего в разреженной атмосфере спутника равно

\(~a_t = \frac{\Delta \upsilon}{\Delta t} = \frac{2\pi F_{sopr} R}{m \upsilon} \frac{\upsilon}{2 \pi R} = \frac{F_{sopr}}{m}. \qquad (5)\)

Отсюда

\(~F_t = ma_t = m \frac{F_{sopr}}{m} = F_{sopr},\)

что и требовалось установить.

Итак, чем больше сопротивление, которое оказывает разреженный газ на спутник при его движении, тем быстрее увеличивается скорость спутника! (Когда катаешься на санках с горки, такое и не приснится. Кстати, подумайте, почему. Ведь санки и спутник двигаются в одном и том же поле гравитации Земли.)

Найдем теперь уменьшение радиуса орбиты ΔR на одном витке. Связь между ΔR и Δυ легко получается из формулы (1):

\(~\Delta \upsilon = -\frac{\upsilon}{2R} \Delta R,\)

а величину Δυ мы уже определили. Поэтому получаем

\(~\frac{\Delta R}{R} = -\frac{4\pi F_{sopr}}{mg}. \qquad (6)\)

Заметим, что относительное уменьшение высоты полета точно в два раза превышает соответствующее увеличение относительной скорости спутника.

Рис. 2

Обратим внимание на формулу (6). Если мысленно развернуть окружность радиусом R и траекторию спутника на одном витке полета в прямые отрезки АВ и АС (рис. 2), расположив их так, чтобы отрезок ВС был равен по величине \(~\Delta R = -\frac{4\pi F_{sopr} R}{mg}\), то станет ясно, что в разреженной атмосфере в каждой точке орбиты касательная к траектории полета спутника образует с местной горизонталью малый, но отличный от нуля угол

\(~\alpha \approx \operatorname{arctg} \frac{4\pi F_{sopr} R}{mg \cdot 2\pi R} = \frac{4F_{sopr}}{mg}.\)

Угол этот не постоянный, а зависит от силы сопротивления среды и, следовательно, от высоты полета спутника. Чем сильнее тормозится тело, тем больше этот угол. Формально спутник двигается как тело, соскальзывающее с наклонной плоскости, причем составляющая силы тяжести вдоль наклонной плоскости равна \(~mg \sin \alpha \approx 2F_{sopr}\), т.е. удвоенной силе сопротивления среды. Если векторно сложить эту силу с силой сопротивления среды, направленной против движения спутника, то результирующая сила окажется равной по величине F_sopr и ускоряющей спутник в направлении вперед. Вот вам и объяснение аэродинамического парадокса.

Внимательный читатель, наверное, уже заметил, что аэродинамический парадокс, в том виде, как он был сформулирован, обязан замечательной особенности, которая есть у гравитационного (и кулоновского) поля, где полная энергия тела равна кинетической, взятой со знаком «минус». К примеру, если бы сила притяжения спутника к Земле зависела от R как \(~\frac{1}{R^3}\), то в разреженной атмосфере тангенциальное ускорение спутника равнялось бы \(~\frac{F_{sopr}}{3m}\). (Движение спутника в общем случае степенной зависимости силы притяжения от радиуса в разреженной атмосфере рассматривается в упражнении 4.)

Расчеты ускорения спутника были выполнены на основе баланса энергии спутника в гравитационном поле с учетом работы внешней силы сопротивления. Этот же результат можно получить другим путем, не прибегая к закону сохранения энергии, а используя уравнение для скорости изменения момента импульса \(~L = m \upsilon R\) спутника на круговой орбите:

\(~\frac{\Delta L}{\Delta t} = M, \qquad (7)\)

где \(~M = -F_{sopr} R\) — момент внешней силы (силы сопротивления среды), уменьшающий момент импульса спутника при его торможении в атмосфере и спуске с высокой орбиты на низкую. Пусть ΔL — изменение момента импульса спутника за один виток орбиты. Как и раньше, считаем, что плотность газа на орбите столь мала, что сила F_sopr приводит к малому возмущению орбиты на одном витке. Имеем\[~\Delta L = m \upsilon \Delta R + m \Delta \upsilon R\], откуда из уравнения (7) и выражения \(~\Delta \upsilon = -\upsilon \frac{\Delta R}{2R}\), справедливого в случае ньютоновского поля тяготения, сразу же получаются те же самые результаты для Δυ, ΔR и a_t.

Уравнение моментов (7) позволяет упростить решение многих задач о движении спутника в гравитационном поле с центральной симметрией, потому что в этом случае не надо учитывать момент силы тяжести — вектор этой силы проходит через центры масс спутника и Земли и ее момент равен нулю.

Аэродинамический парадокс спутника и связанные с этим явлением вопросы имеют важное прикладное значение. Рассмотрим несколько примеров.

Пример 1. Плотность атмосферы на больших высотах

Наблюдения за торможением спутников позволяют определить профиль плотности атмосферы на таких высотах, куда не могут подняться самолеты и воздушные шары-зонды.

Действительно, если единственная сила, изменяющая момент импульса спутника, — это сила сопротивления \(~F_{sopr} = C_x \frac{\rho \upsilon^2}{2} S_x\), где ρ = ρ(R) — неизвестная функция радиуса орбиты R или высоты полета h = R - R₀, то из уравнения моментов (путем несложных математических преобразований, с которыми вы сможете справиться самостоятельно) получаются уравнения для определения функции ρ(R) по наблюдениям за скоростью уменьшения радиуса орбиты \(~\frac{dR}{dt}\) или периода обращения спутника \(~\frac{dT}{dt}\) на разных высотах:

\(~\rho(R) = -\frac{1}{2C \upsilon R} \frac{dR}{dt}, \qquad (8)\) \(~\rho(R) = -\frac{1}{6\pi CR} \frac{dT}{dt}, \qquad (8)\)

где \(~C = \frac{C_x S_x}{2m}\) — постоянный множитель, который называют баллистическим коэффициентом спутника (он имеет размерность м²•кг^-1). Формулы (8) и (9) справедливы для круговых орбит на больших высотах, когда взаимодействие спутника с молекулами газа лишь слегка возмущает орбиту.

До запуска искусственных спутников Земли сведения об атмосфере на больших высотах добывались только на основе астрономических и (какое-то время) с помощью радиолокационных наблюдений за движением метеоритов и метеоракет. Навигационные возможности спутников, и прежде всего наличие на спутнике радиопередатчика и автономных навигационных приборов, а также использование наземных ЭВМ качественно изменили задачу слежения за параметрами орбиты тела в окрестностях Земли. Благодаря многочисленным наблюдениям за полетами искусственных спутников на разных высотах, вхождением аппаратов в плотные слои атмосферы, сейчас имеется обширная информация о плотности газа верхней атмосферы, ее зависимости от времени года, суток, широты, солнечной активности и т.д.

Очевидно, что эксперименты по определению плотности газа атмосферного «хвоста» планеты удобнее проводить на спутниках шарообразной формы, когда площадь сечения S_x, и следовательно, баллистический коэффициент С, не зависит от ориентации спутника. Именно такую форму имели американские спутники-зонды серии «Эксплорер». К тому же, они были сделаны специально пустотелыми, что увеличивало эффективность их торможения в разреженном газе при зондировании земной атмосферы, которое проводилось в широком диапазоне высот — вплоть до 1000 км, где плотность газа меньше 10^-13 — 10^-15 кг/м³.

Пример 2. Последний виток

Оценим, на какую высоту Δh = ΔR снижается спутник в разреженной атмосфере за один виток полета. Пусть спутник имеет массу 10³ кг и площадь миделевого сечения 1 м², а на высоте 200 км плотность воздуха в среднем составляет 4•10^-10 кг/м³. Из формулы (6) получаем

\(~\Delta R = \frac{4 \pi \rho \upsilon^2 S_x R}{mg}\) ≈ 2 км.

На первый взгляд, ΔR вроде бы малая величина, и вектор скорости спутника в каждой точке траектории полета на этой высоте отклоняется от местной горизонтали на ничтожно малый угол

\(~\alpha \approx \frac{2 \rho \upsilon^2 S_x}{mg}\) ≈ 5•10^-6 рад ≈ 1.

Однако за сутки спутник совершает более 16 оборотов, и, спускаясь все ниже и ниже, где плотность атмосферы очень резко возрастает, он все круче и круче «зарывается» в атмосферу Земли. На высоте 150 км, где ρ = 4•10^-9 кг/м³, за один виток этот же спутник снизится на 20 км! Еще один-два витка, и спутник попадает в столь плотную воздушную среду, что не может завершить очередной виток и, вместо того чтобы двигаться по спирали, начинает падать почти отвесно, испытывая при этом большие механические нагрузки и тепловой удар. Наступает неминуемый конец его орбитального путешествия. Легкие, пустотелые спутники падают раньше, сходят с орбиты на больших высотах, тяжелым удается вращаться вокруг Земли ближе к ее поверхности.

Рис. 3

На рисунке 3 показано, как критическая высота и, соответственно, критическое время обращения спутника вокруг Земли зависят от его баллистического параметра С. Например, корабль «Восток», на котором летал Юрий Гагарин, имел массу 2,4 т и диаметр 2,3 м, т.е. баллистический коэффициент корабля был равен С = 1,7•10^-3 м²•кг^-1. Как видно из графика, критическая высота полета составляет h_кр ≈ 130 км, а критическое время обращения — T_кр ≈ 86 мин 54 с. Спутник, о котором шла речь выше, имеет примерно такое же отношение \(~\frac{S_x}{m}\), как корабль «Восток», и близкие критические параметры орбиты, в частности — критическая высота полета спутника составляет около 125 км. Заметим, что для ледяного шарика диаметром 1 см критическая высота превышает 200 км, а для меньших частиц она еще больше! Атмосфера и Земля работают как пылесос, исправно удаляя мелкий космический мусор с околоземных орбит.

И еще одно. Когда спутник, спускаясь, приближается к критической высоте, сила сопротивления среды все еще не так велика по сравнению с силой тяжести спутника. Она примерно во столько же раз меньше нее, во сколько эффективная толщина атмосферы меньше радиуса Земли, умноженного на 4π (см. формулу (6)), т.е. составляет примерно десятитысячную часть от силы тяжести. Мало? Но этого уже достаточно, чтобы спутник очень скоро исчез.

Пример 3. Время жизни спутника в орбитальном полете

Протяженный атмосферный «хвост» укорачивает жизнь спутника. Формулы, которые есть в нашей статье, позволяют сделать оценку времени жизни спутника, если известны начальная высота полета и высотный профиль плотности атмосферы. Хотя проведение точных расчетов — достаточно трудоемкая операция, в приближенных оценках можно учитывать, что основное время жизни спутника связано с нахождением его на самых верхних орбитах, где плотность воздуха наименьшая. Результаты оценок зависят от типа спутника, точнее — от его баллистического параметра С. Не будем здесь рассматривать само решение этой задачи (тем более что один из ее вариантов опубликован в журнале «Квант» №2 за 1996 год в статье «V Международная олимпиада «Интеллектуальный марафон» - см. задачу 3 по физике), а только приведем в форме таблицы результаты оценочных величин времени жизни обычных исследовательских спутников на орбитах с разными начальными высотами полета:

Высота полета (км)	150	190	210	230	400	500	650	850	1300	2000
Время жизни	1 сутки	2 суток	1 неделя	1 месяц	1 год	10 лет	100 лет	1000 лет	10 тыс.лет	100 тыс.лет

Эта таблица иллюстрирует, прежде всего, сколь резко убывает плотность воздуха на больших высотах при удалении от земной поверхности. Таблица помогает также ответить на вопрос, почему спутник, на борту которого устанавливается аппаратура, рассчитанная на многолетнюю программу исследований, выводится на орбиту высотой не менее 500 км.

В заключение предлагаем несколько задач и вопросов для самостоятельной работы.

Упражнения

1. Первые запуски спутников продемонстрировали нечто любопытное. При выводе на орбиту и отделении спутника от последней ступени ракеты-носителя ракета с уже выключенными двигателями обгоняла спутник и вырывалась вперед. Как объяснить это явление? Можно считать, что в момент отделения скорости ракеты и спутника одинаковые.
2. Объясните, почему из-за торможения спутника в верхних слоях атмосферы его первоначально эллиптическая орбита стремится стать круговой.
3. Покажите, что если бы плотность воздуха убывала с высотой по закону \(~\rho \sim R^{-\frac 12}\), где R — расстояние от центра планеты, то скорость уменьшения радиуса орбиты спутника была бы постоянной.
4. Спутник вращается по окружности в поле планеты с разреженной атмосферой. Предположим, что сила притяжения к планете подчиняется закону \(~F \sim R^{-n}\), где n — произвольное положительное число (случай n = 2, как известно, соответствует ньютоновскому тяготению). При каких и возможен аэродинамический парадокс спутника?
5. Зависит ли торможение спутника на больших высотах от температуры воздуха?
6. Допустим, что в результате сильного нагрева Земли вся вода в океанах испарилась, а планета покрылась плотной и горячей атмосферой из водяного пара. Как это скажется на движении существующих ныне искусственных спутников Земли и ее естественного спутника Луны?

Ответы

1. Такое явление наблюдается, когда на орбитальное движение тела влияет сопротивление разреженного атмосферного воздуха. Суть дела в том, что, двигаясь в разреженном газе, компактный спутник, укомплектованный научными приборами или другим оборудованием, испытывает меньшее сопротивление, чем сравнительно большая по размерам пустотелая ракета с отработанными двигателями. У ракеты больший баллистический коэффициент С, или, как иногда говорят, большая парусность, чем у спутника. Вот почему аэродинамический парадокс выражен более ярко для ракеты, нежели для спутника, который падает на Землю в разреженной атмосфере медленнее и по более пологой траектории. Таким образом, спутник заметно отстает от ракеты, хотя последняя испытывает большее торможение в разреженной атмосфере, чем спутник.
2. Движение спутника по эллиптической орбите, пересекающей верхние разреженные слои атмосферы, имеет интересную особенность. В перигее спутник, испытывая максимальное сопротивление, теряет в скорости на каждом витке, и, тем самым, его апогей уменьшается. В апогее торможение спутника меньше, чем в перигее, особенно если орбита заметно вытянута. Поэтому перигей не снижается так сильно, как апогей, т.е. орбита действительно стремится к круговой. (Точное решение задачи о движении спутника достаточно сложное, так как требуется учитывать еще изменение скорости спутника на каждом витке вследствие его падения в поле тяжести Земли.)
3. Указание. Воспользуйтесь уравнением моментов (7).
4. Допустим, что сила притяжения спутника к планете определяется выражением \(~F = \frac{A}{R^n}\), где А — постоянная. Из уравнения \(~\frac{m \upsilon^2}{R} = \frac{A}{R^n}\) найдем выражение для кинетической энергии спутника:

   \(~W_k = \frac{m \upsilon^2}{2} = \frac{A}{2R^{n - 1}}.\)

   Для заданного поля сил потенциальная энергия спутника равна

   \(~W_p = - \frac{A(n - 1)}{R^{n - 1}},\)

   а полная энергия составляет

   \(~W_0 = \frac{A}{2R^{n - 1}} (3 - 2n) = W_k (3 - 2n).\)

   Баланс полной энергии спутника в начале и в конце витка с учетом работы силы сопротивления F_sopr приводит к такому выражению для тангенциального ускорения пролетающего в разреженной атмосфере спутника:

   \(~a_t = \frac{F_{sopr}}{m (2n - 3)}.\)

   Отсюда очевидно, что при n > 1,5 можно говорить об аналоге аэродинамического парадокса спутника в гравитационном поле.

5. Так как орбитальная скорость спутника во много раз превышает среднюю тепловую скорость молекул, находящихся в верхних слоях атмосферы, при расчетах сил торможения спутника мы не учитывали собственное движение частиц среды. Казалось бы, торможение спутника на больших высотах не должно зависеть от температуры воздуха Т. Однако это не так. Дело в том, что при изменении температуры изменяется плотность газа — с ростом температуры плотность возрастает. Увеличивается также характерная толщина атмосферы \(~\Delta h \approx \frac{RT}{Mg}\), на которой давление газа изменяется в е раз (здесь R — универсальная газовая постоянная, М — молярная масса воздуха, g — ускорение свободного падения). Вариации плотности газа из-за изменения температуры сказываются на торможении спутника.
6. Мы знаем, что если бы на Земле не было гор и впадин, а вода всего мирового океана равномерно покрывала земной шар, то глубина этого океана была бы около 2 км. Давление на дне достигало бы величины 200 атм. Чтобы при таком давлении превратить воду в пар, требуется ее нагреть до температуры чуть больше 600 К — именно такой должна быть минимальная температура атмосферы Земли, чтобы вся свободная вода на Земле существовала в виде пара. В этом случае Земля будет окружена толстой и плотной атмосферой водяного пара высотой в сотни километров. Для такой атмосферы характерный перепад высот, на котором атмосферное давление уменьшается в е раз, будет около 30 км (т.е. в 3 раза больше). Из-за плотного атмосферного «хвоста» водяного пара станет невозможным полет спутников на сравнительно низких орбитах, на которых они сейчас летают. В то же время для таких удаленных объектов, как Луна, влияние земной атмосферы из водяного пара на орбитальные движения будет все же пренебрежимо малым.