KC. Несколько сил

Движение под действием нескольких сил

В механике используются следующие виды сил:

• Гравитационная сила \(~\left(\vec{F}_{тяг} \right)\). Разновидность: сила тяжести \(~\left(\vec{F}_{т} ,\; \; m\cdot \vec{g}\right)\).

Направление. Гравитационная сила направлена вдоль линии, соединяющей центры масс взаимодействующих тел (рис. 1, а). Сила тяжести направлена вертикально вниз, к центру Земли (рис. 1, б).

Формулы\[~F_{тяг} =G\cdot \dfrac{m_{1} \cdot m_{2} }{R^{2} } ,\; \; \; F_{т} =G\cdot \dfrac{M_{пл} \cdot m}{r^{2} } ,\; \; \; F_{т} =m\cdot g.\]

Рис. 1а

Рис. 1б

• Сила упругости \(~\left(\vec{F}_{упр} \right)\). Разновидности: сила реакции опоры \(~\left(\vec{N}\right)\) и сила натяжения подвеса \(~\left(\vec{T}\right)\).

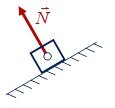
Направление. Сила упругости направлена в сторону, противоположную перемещению частей тела при деформации. Сила реакции опоры перпендикулярна поверхностям соприкасающихся тел (рис. 1, в), сила натяжения подвеса направлена вдоль оси подвеса (рис. 1, г).

Формула\[~F_{упр} =k\cdot \Delta l\].

Рис. 1в

Рис. 1г

• Сила трения \(~\left(\vec{F}_{тр} \right)\). Разновидность: сила трения покоя \(~\left(\vec{F}_{тр пок} \right)\), сила трения скольжения \(~\left(\vec{F}_{тр ск} \right)\) и сила сопротивления \(~\left(\vec{F}_{с} \right)\).

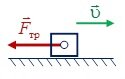
Направление. Вдоль поверхности соприкосновения тел, против относительной скорости (рис. 1, д).

Формулы\[~F_{тр пок} \le \mu \cdot N,\, \, \, \, F_{тр ск} =\mu \cdot N\].

Рис. 1д

• Архимедова сила \(~\left(\vec{F}_{арх} \right)\).

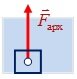
Направление. Архимедова сила направлена вертикально вверх (против направления ускорения свободного падения слоев жидкости) (рис. 1, е).

Формула\[~F_{арх} =\rho _{ж} \cdot g\cdot V_{погр} \].

Рис. 1е

• Сила тяги \(~\left(\vec{F}\right)\).

Направление. Сила тяги направлена так, как указано в условии. Для двигателей, по умолчанию, эта сила направлена вдоль поверхности (рис. 1, ж).

Рис. 1ж

Эти силы возникают в результате:

• взаимодействия с телами большой массы (спутники, планеты, кометы) — гравитационная сила или сила тяжести;

• взаимодействия с деформированными телами (пружина, опора, подвес) — сила упругости, сила реакции опоры, сила натяжения подвеса;

• взаимодействия с твердой, не гладкой поверхностью — силы сухого трения. Причем если тело покоится относительно поверхности — это сила трения покоя, если движется — сила трения скольжения;

• движения в жидкости или газе — силы сопротивления;

• взаимодействия с жидкостью или газом, плотность которых соизмерима с плотностью тела — архимедова сила;

• работы человека, животного, механизма — сила тяги.

Задачи, в которых на тело действуют несколько сил, решайте, придерживаясь следующего плана решения:

1. Сделайте чертеж. Укажите все действующие на тело силы, укажите направления скорости и ускорения. Изобразите оси координат.
2. Запишите второй закон Ньютона в векторном виде и в проекциях на оси координат:

   \(~m\cdot \vec{a}=\vec{F}_{1} +\vec{F}_{2} +\vec{F}_{3} + \dots ,\)

   \(~OX: m \cdot a_x = F_{1x} + F_{2x} + F_{3x} + \dots ,\)

   \(~OY: m \cdot a_y = F_{1y} + F_{2y} + F_{3y} + \dots \)

3. Определите значения проекций всех величин.
4. Решите полученные уравнения. При необходимости, исходя из физической природы, выразите силы через величины, от которых они зависят.

• Если в условии задачи говорится о системе материальных тел, то необходимо записывать уравнение второго закона Ньютона для каждого тела системы в отдельности.

• Можно выбирать разные системы координат для разных тел.

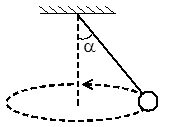
Систему, изображенную на рис.2, а, называют коническим маятником — тело вращается в горизонтальной плоскости; на рис. 2, б показан математический маятник — тело вращается в вертикальной плоскости.

• Скорость конического маятника не меняется по величине, поэтому есть только центростремительное ускорение;

• скорость математического маятника изменяется по величине, поэтому есть и центростремительное ускорение, направленное к центру окружности (вдоль подвеса), и тангенциальное ускорение, направленное также как и скорость (по касательной), если скорость увеличивается, и в противоположную сторону, если скорость уменьшается.

Рис. 2а

Рис. 2б

Движение в неинерциальной системе отсчета (НИСО)

Если тело находится в системе, которая движется с ускорением, то можно применять несколько способ решения задач:

1 способ. Второй закон Ньютона записать в следующем виде:

\(~m\cdot \vec{a}_{т} =\vec{F}_{1} +\vec{F}_{2} +...,\)

где \(~\vec{a}_{т} =\vec{a}_{с} +\vec{a}_{т/с} ,\, \, \, \vec{a}_{т} \) — ускорение тела относительно неподвижной системы (Земли), \(~\vec{a}_{с} \) — ускорение системы, в которой находится тело, \(~\vec{a}_{т/с} \)} — ускорение тела относительно движущейся системы.

2 способ. Перейти в НИСО, тогда второй закон Ньютона будет иметь вид

\(~m\cdot \vec{a}_{т/с} =\vec{F}_{ин} +\vec{F}_{1} +\vec{F}_{2} + ...,\)

где \(~\vec{a}_{т/с} \) — ускорение тела относительно движущейся системы, \(~\vec{F}_{ин} \) — сила инерции, которая направлена против ускорения системы ас, а по величине равна Fин = т•ас, \(~\vec{a}_{с} \) — ускорение системы.

Немного кинематики:

• Проекция вектора положительна, если составляющая вектора на данную ось направлена вдоль этой оси, отрицательна — если против оси, равна нулю — если вектор перпендикулярен оси.

• При прямолинейном движении ускорение при торможении направлено против скорости.

• При остановке конечная скорость равна нулю.

• При равномерном движении по окружности тело движется с центростремительным ускорением, направленным к центру окружности и равным \(~a_{ц} =\dfrac{\upsilon ^{2} }{R} =\omega ^{2} \cdot R\).

Математика

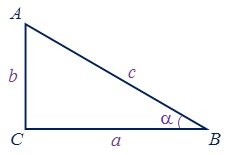
Для прямоугольного треугольника ABC (рис. 3):

\(~\begin{array}{c} {CB=AB\cdot \cos \alpha ,\; \; \; CA=AB\cdot \sin \alpha ,\; \; \; \; CA=CB\cdot {\rm tg}\; \alpha ,} \\ {a=c\cdot \cos \alpha ,\; \; \; b=c\cdot \sin \alpha ,\; \; \; \; b=a\cdot {\rm tg}\; \alpha .} \end{array}\)

Рис. 3

Для прямоугольного треугольника BAC (рис. 4):

\(~\angle ABC=90{}^\circ -\angle ACB,\; \; \; \beta =90{}^\circ -\alpha .\)

Для прямоугольного треугольника AOB (см. рис. 4):

\(~\angle BAO=90{}^\circ -\angle ABO=90{}^\circ -\beta =90{}^\circ -\left(90{}^\circ -\alpha \right)=\alpha .\)

Рис. 4