A. Формула линзы

Формула линзы. Линейное увеличение линзы

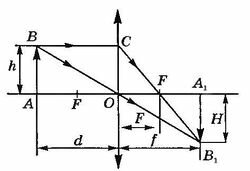
Из подобия треугольников A₁B₁F и OCF (рис. 16.47) следует \(\frac{A_1B_1}{CO}=\frac{A_1F}{OF}.\)

Аналогично из подобия \(\Delta ABO\) и \(\Delta A_1 B_1 O\) \[\frac{A_1B_1}{AB}=\frac{A_1O}{AO}.\] Учитывая, что АВ = СО, из этих равенств получим \(\frac{A_1F}{OF}=\frac{A_1O}{OA} \Rightarrow \frac{f-F}{F}=\frac{f}{d} \Rightarrow \frac{f}{F}-1=\frac{f}{d}.\)

Разделим все слагаемые на f получим \(\frac{1}{F}=\frac{1}{d}+\frac{1}{f}.\) В общем случае \(\pm \frac{1}{F}=\pm \frac{1}{d}\pm \frac{1}{f}.\) —— формула тонкой линзы.

Рис. 16.47

В ней F берут со знаком "+" для собирающей линзы и со знаком "-" для рассеивающей линзы, f — со знаком "+", если изображение действительное, и со знаком "-", если оно мнимое, d — со знаком "+" для действительного предмета и "-" для мнимого предмета. 

Линейное увеличение линзы Г — отношение линейных размеров изображения Н к линейным размерам предмета h:

\(\Gamma=\frac{H}{h}.\)

Из треугольников АВО и А₁В₁О \(\frac{A_1B_1}{AB}=\frac{A_1O}{AO}.\) Тогда \(\frac{H}{h}=\frac{f}{d}.\) Следовательно, увеличение линзы \(\Gamma=\frac{f}{d}.\)

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 481-482.