A. Основные следствия

Основные следствия теории относительности и их экспериментальная проверка

Согласно первому постулату СТО все физические законы не зависят от конкретного выбора инерциальной системы отсчета, поэтому уравнения, представляющие математическую запись физических законов, должны быть инвариантны относительно преобразований Лоренца (преобразования Лоренца устанавливают соотношения между координатами и временем одного и того же события в двух инерциальных системах отсчета — неподвижной К и подвижной К' движущейся относительно системы К со скоростью \(\upsilon\)).

В преобразованиях Лоренца изменяются не только координаты, но и время, которое не считается текущим одинаково во всех инерциальных  системах отсчета. В простейшем случае, когда система К' движется равномерно и прямолинейно вдоль оси X (рис. 18.1), преобразования Лоренца для координат и времени следующие:

\(x' = \frac{(x-\upsilon t)}{\sqrt{1 - \frac{\upsilon^2}{c^2}} }; y' = y ; z' = z ; t' = \frac{t - \frac{\upsilon x}{c^2} }{\sqrt{1 - \frac{\upsilon^2}{c^2}} }\) (18.1)

Рис. 18.1

При движении тел и систем отсчета со скоростями, много меньшими, чем скорость света в вакууме, преобразования Лоренца переходят в преобразования Галилея.

Если \(~\upsilon \ll c,\) то \(\frac{\upsilon}{c} \ll 1 .\) Тогда \(~x' = x - \upsilon t ; y' = y ; z' = z ; t = t'.\)

Следовательно, классическая (ньютоновская) механика является частным случаем СТО. При \(~\upsilon \ge c\) величины х' и t' теряют физический смысл (становятся мнимыми). Это находится в соответствии с тем, что движение со скоростью \(~\upsilon>c\) невозможно.

Из постулатов СТО вытекает несколько основных следствий.

1. Относительность одновременности.

Согласно классической механике два события, одновременные в одной инерциальной системе отсчета, будут одновременны и в любой другой инерциальной системе отсчета, так как ход времени одинаков во всех точках пространства и во всех инерциальных системах отсчета.

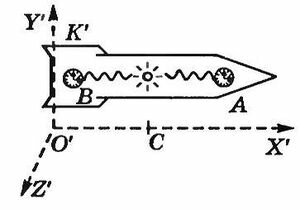
Второй постулат СТО отвергает гипотезу абсолютной одновременности разноместных событий. Одновременность пространственно разделенных событий относительна: события, являющиеся одновременными в одной инерциальной системе отсчета, не одновременны в других инерциальных системах, движущихся относительно первой. Чтобы убедиться в этом, рассмотрим следующий мысленный эксперимент. Допустим, что космонавт хочет сравнить ход часов А и В, установленных на противоположных концах космического корабля — синхронизировать часы (рис. 18.2). Очевидно, это проще всего сделать с помощью светового сигнала. Мысленно выполним наблюдение за этим процессом с точки зрания двух ИСО — К', связанной с кораблем, и ИСО К, относительно которой корабль движется. Для этого с помощью источника, неподвижного относительно корабля и расположенного в его середине, космонавт производит вспышку света. Свет одновременно достигает обоих часов. Если показания часов в этот момент одинаковы, то часы идут синхронно.

Рис. 18.2

Но так будет лишь относительно системы К', связанной с кораблем. В системе же отсчета К, относительно которой корабль движется, положение иное. Часы на носу корабля удаляются от того места, где произошла вспышка света источника, и, чтобы достигнуть часов А, свет должен преодолеть расстояние, большее половины длины корабля (рис. 18.3, а, б). Напротив, часы В на корме приближаются к месту вспышки, и путь светового сигнала меньше половины длины корабля. Поэтому наблюдатель в системе К придет к выводу, что сигналы достигают обоих часов неодновременно. Это можно доказать, используя преобразования Лоренца. Если события в системе К пространственно разделены \(~(x_1 \ne x_2),\) но одновременны \(~(t_1 = t_2 = t),\) то в системе К' согласно преобразованиям Лоренца (18.1)

\(x_1' = \frac{x_1 - \upsilon t}{ \sqrt{1 - \frac{\upsilon^2}{c^2}} }; x_2' = \frac{x_2 - \upsilon t}{ \sqrt{1 - \frac{\upsilon^2}{c^2}} };\) \(t'_1 = \frac{ t - \frac{\upsilon x_1}{c^2} }{ \sqrt{1 - \frac{\upsilon^2}{c^2}} } ; t'_2 = \frac{ t - \frac{\upsilon x_2}{c^2} }{ \sqrt{1 - \frac{\upsilon^2}{c^2}} }\)

Рис. 18.3

Откуда \(~x_1' \ne x_2' , t_1' \ne t_2'\) т.е. события, оставаясь пространственно разделенными, оказываются и неодновременными.

Два любых события в точках А и В, одновременные в системе К' , неодновременны в системе К. Но в силу принципа относительности системы К' к К совершенно равноправны. Ни одной из этих систем нельзя отдать предпочтение. Поэтому мы и вынуждены прийти к заключению, что одновременность пространственно разделенных событий относительна. Причиной относительности одновременности является конечность скорости распространения сигналов.

2. Относительность промежутков времени.

Относительность одновременности событий приводит к тому, что дли-тельность (промежуток времени) в разных инерциальных системах отсчета также будет различна.

Длительностью (промежутком времени) между двумя событиями называется время, прошедшее между этими событиями, измеренное часами, расположенными в данной системе отсчета. Пусть в точке А, неподвижной относительно системы К' в моменты времени t'₁ и t'₂ произошли два события. Например, математический маятник дважды прошел положение равновесия. Промежуток времени \(~\tau_0\) между этими событиями \(~\tau_0 = t_2' - t_1'\) где t'₁ и t'₂ — время, отсчитываемое по часам системы К'. Время, измеряемое на часах в той ИСО, где они покоятся, называется собственным временем. Собственное время отсчитывается по часам, движущимся вместе с системой отсчета. В системе К, относительно которой движется система К'у промежуток времени \(~\tau\) между двумя событиями, происшедшими в точке А, равен \(~\tau = t_2 - t_1 ,\) t₁ и t₂ — время, отсчитываемое по часам системы К.

Согласно преобразованиям Лоренца

\(t'_2 = \frac{ t_2 - \frac{\upsilon x_2}{c^2} }{ \sqrt{1 - \frac{\upsilon^2}{c^2}} } ; t'_1 = \frac{ t_1 - \frac{\upsilon x_1}{c^2} }{ \sqrt{1 - \frac{\upsilon^2}{c^2}} }\)

тогда

\(\tau_0 = t'_2 - t'_1 = \frac{ (t_2 - t_1) - \frac{ \upsilon(x_2 - x_1) }{c^2} }{ \sqrt{1 - \frac{\upsilon^2}{c^2}} } = \frac{ \tau - \frac{ \upsilon(x_2 - x_1) }{c^2} }{ \sqrt{1 - \frac{\upsilon^2}{c^2}} }.\)

Так как \(~x_2 - x_1\) есть смещение вдоль оси ОХ за время \(~\tau\) в системе отчета К, в которой происходили эти события, то \(~x_2 - x_1 = \upsilon \tau.\) Поэтому \(\tau_0 = \tau \sqrt{1 - \frac{\upsilon^2}{c^2}}\) отсюда

\(\tau = \frac{\tau_0}{\sqrt{1 - \frac{\upsilon^2}{c^2}}}\) (18.2)

Таким образом, в движущихся относительно друг друга системах отсчета со скоростью, близкой к скорости света в вакууме, наблюдается эффект замедления времени, т.е. \(~\tau > \tau_0.\)

Длительность явления, происходящего в некоторой точке А пространства, будет наименьшей в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Это значит, что часы, движущиеся относительно инерциальной системы отсчета, идут медленнее неподвижных часов и показывают меньший промежуток времени между событиями. Если же \(~\upsilon \ll c,\) то \(\frac{\upsilon^2}{c^2} \to 0\) и \(~\tau \approx \tau_0,\) т.е. при движении с малыми скоростями эффектом замедления времени можно пренебречь.

Скорости, с которыми нам приходится сталкиваться в повседневной жизни, гораздо меньше скорости света c, поэтому неудивительно, что мы не наблюдаем замедление времени как реальный эффект. Для проверки замедления времени были поставлены специальные эксперименты. Например, в 1971 г. сверхточные атомные часы совершили кругосветный полет на борту реактивного самолета. Так как скорость реактивного самолета ч км (1•10³ км\ч) гораздо меньше скорости света, погрешность хода часов должна была составлять несколько наносекунд, для того чтобы можно было обнаружить эффект замедления времени. Часы обладали требуемой точностью, и предсказания Энштейна о замедлении времени были подтверждены.

Эффект замедления времени подтверждается также наблюдениями над элементарными частицами. Так, например, установлено, что среднее время жизни мюона в состоянии покоя равно 2,2 мкс. Тщательные эксперименты показали, что когда мюон летит со скоростью, близкой к скорости света, его время жизни увеличивается так, как предсказывает формула замедления времени (18.2).

3. Относительность длин (расстояний).

В классической механике считается неопровержимым тот факт, что расстояние между двумя точками тела (например, длина стержня) одинаково во всех инерциальных системах отсчета. В теории же относительности расстояние не является абсолютной величиной: оно зависит от скорости движения тела относительно рассматриваемой системы отсчета.

Пусть l₀ — длина неподвижного стержня в инерциальной системе отсчета К' — собственная длина стержня (длина стержня в системе отсчета, относительно которой тело покоится). Длина l этого же стержня в системе отсчета КУ относительно которой стержень движется со скоростью \(~\upsilon ,\) параллельной оси стержня, равна

\(l = l_0\sqrt{1 - \frac{\upsilon^2}{c^2}} = l_0\sqrt{1-\beta^2}.\) (18.3)

Из последней формулы следует, что \(~l<l_0,\) т.е. в инерциальных системах отсчета, движущихся друг относительно друга со скоростью, близкой к скорости света в вакууме, наблюдается эффект сокращения длины тел. Причем сокращение длины тела наблюдается только в направлении его движения, а поперечные размеры тела остаются неизменными.

Сокращение длины тела не связано с действием каких-либо сил, "сдавливающих" стержень вдоль его длины, это — кинематический эффект, вытекающий из преобразований Лоренца. Действительно, собственная длина стержня в системе К' — это разность координат концов стержня \(~l_0 = x'_2 - x'_1 ,\) а длина l движущегося стержня в системе К равна разности координат его концов \(~l = x_2 - x_1.\)

Подставим значения х'₁ и х'₂ по формуле (18.1):

\(l_0 = \frac{x_2 - \upsilon t}{ \sqrt{1 - \frac{\upsilon^2}{c^2}} } - \frac{x_1 - \upsilon t}{ \sqrt{1 - \frac{\upsilon^2}{c^2}} } = \frac{x_2 - x_1}{ \sqrt{1 - \frac{\upsilon^2}{c^2}} } = \frac{l}{ \sqrt{1 - \frac{\upsilon^2}{c^2}} }.\) Отсюда \(l = l_0 \sqrt{1 - \frac{\upsilon^2}{c^2}}.\)

Из преобразований Лоренца следует также, что \(~y'_2 - y'_1 = y_2 - y_1 \) и \(~z'_2 - z'_1 = z_2 - z_y,\) т.е. поперечные размеры тела не зависят от скорости движения.

Если же \(~\upsilon \ll c,\) то \(~\beta \to 0\) и \(~l \approx l_0,\) т.е. при движении с малыми скоростями эффекта сокращения длины не наблюдается.

Рассмотренные выше эффекты называются релятивистскими, так как они наблюдаются при скоростях движения, близких к скорости света, и описываются СТО, но не могут быть объяснены с позиций классической физики. 

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 542-546.