A. Лучи в призме

Ход лучей в призме

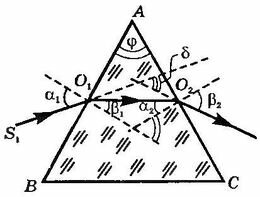
Монохроматический свет падает на грань АВ стеклянной призмы (рис. 16.28), находящейся в воздухе, S₁O₁ — падающий луч, \(~\alpha_1\) — угол падения, O₁O₂ — преломленный луч, \(~\beta_1\) — угол преломления. Так как свет переходит из среды оптически менее плотной в оптически более плотную, то \(~\beta_1<\alpha_1.\) Пройдя через призму, свет падает на ее грань АС. Здесь он снова преломляется\[~\alpha_2\] — угол падения, \(~\beta_2\) — угол преломления. На данной грани свет переходит из среды оптически более плотной в оптически менее плотную. поэтому \(~\beta_2>\alpha_2.\)

Грани ВА и СА, на которых происходит преломление света, называются преломляющими гранями. Угол \(\varphi\) между преломляющими гранями называется преломляющим углом призмы. Угол \(~\delta\), образованный направлением луча, входящего в призму, и направлением луча, выходящего из нее, называют углом отклонения. Грань, лежащая против преломляющего угла, называется основанием призмы.

Для призмы справедливы следующие соотношения:

1) Для первой преломляющей грани закон преломления света запишется так:

\(\frac{\sin \alpha_1}{\sin \beta_1}=n,\)

где n — относительный показатель преломления вещества, из которого сделана призма.

2) Для второй грани:

\(\frac{\sin \alpha_1}{\sin \beta_1}=\frac{1}{n}.\)

3) Преломляющий угол призмы:

\(\varphi=\alpha_2 + \beta_1.\)

Угол отклонения луча призмы от первоначального направления:

\(\delta = \alpha_1 + \beta_2 - \varphi.\)

Следовательно, если оптическая плотность вещества призмы больше, чем окружающей среды, то луч света, проходящий через призму, отклоняется к ее основанию. Несложно показать, что если оптическая плотность вещества призмы меньше, чем окружающей среды, то луч света после прохождения через призму отклонится к ее вершине.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 469-470.