A. Когерентность
Интерференция света. Когерентность. Спектральное разложение при интерференции
Интерференция является характерным признаком волновых процессов любой природы.
Интерференция возникает при наложении когерентных волн. Когерентные волны — это волны одинаковой частоты \(~(\upsilon_1 = \upsilon_2),\) с постоянной разностью фаз \(~(\varphi_2 - \varphi_1 = const),\) колебания векторов напряженности в которых происходят в одной плоскости.
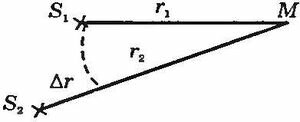
Пусть в точечных когерентных источниках S1 и S2 колебания векторов \(\vec E\) происходят в одинаковых фазах. Волны от этих источников до точки М (рис. 17.3) распространяются в одной среде. От источника S1 приходит в точку М волна
от источника S2 приходит волна
где r1 и r2 — расстояния от источников S1 и S2 до точки М. Для нахождения амплитуды Е0 результирующей световой волны в точке М, возникающей в результате наложения этих волн, воспользуемся методом векторных диаграмм (рис. 17.4):
Амплитуда результирующего колебания зависит от разности фаз - \((\varphi_1 - \varphi_2)\). Разность фаз
зависит, как видно, от геометрической разности хода \(~(r_2 - r_1)\) если волны распространяются в разных средах, надо учитывать оптическую разность хода. Оптической длиной пути называется произведение геометрической длины r пути световой волны в данной среде на абсолютный показатель преломления этой среды\[~L = nr.\] Оптическая разность хода волн \(~\Delta = n_2 r_2 - n_1 r_1,\) где \(~n_2\) и \(~n_1\) — абсолютные показатели преломления этих сред. Так как волны когерентны, то \(\Delta \varphi\) имеет постоянное во времени (но свое для каждой точки пространства) значение. Интенсивность света \(~I\) пропорциональна \(~I \sim E^2 ,\) поэтому уравнение (17.1) можно переписать в виде
Для некогерентных волн разность фаз
непрерывно изменяется со временем, поэтому среднее значение за период \( < \cos \Delta \varphi > = 0,\) и интенсивность результирующей волны всюду одинакова и равна \(~I = I_1 + I_2 ,\) и если \(~I_1 = I_2 ,\) то \(~I = 2I_1.\)
Для когерентных волн в точках пространства, где \( \cos \Delta \varphi > 0,\) \(~I > I_1 + I_2 ,\) где \(\cos \Delta \varphi < 0,\) интенсивность \(~I < I_1 + I_2.\) Следовательно, при наложении двух когерентных световых волн происходит пространственное перераспределение энергии по волновому фронту, в результате чего в пространстве образуется устойчивая картина чередования областей максимумов и минимумов интенсивности. Но среднее значение энергии во всех точках наблюдаемой картины равно, конечно, сумме энергий, приносимых обеими волнами.
Если разность фаз \(\Delta \varphi = \frac{2 \pi (r_2 - r_1)}{\lambda} = m \cdot 2 \pi,\) то
Таким образом, если разность хода в вакууме равна целому числу длин волн, то \(~\cos \Delta \varphi = 1\) и \(I = I_1 + I_2 + 2\sqrt{I_1I_2}.\) Если \(I_1 = I_2,\) то \(I = 4I_1,\) интенсивность света будет максимальна (колебания, возбуждаемые в точке М обеими волнами, находятся в одинаковых фазах и усиливают друг друга).
Равенство (17.2) есть условие интерференционного максимума.
Если \(\Delta \varphi = \frac{2 \pi(r_2 - r_1)}{\lambda} = (2m+1) \pi,\) то \(\cos \Delta \varphi = -1\) и \(I = I_1 + I_2 - 2\sqrt{I_1I_2}.\)
Если \(~I_1=I_2,\) то \(~I=0,\) т.е. интенсивность света минимальна (колебания, возбуждаемые в точке М обеими волнами, находятся в противофазе и ослабляют друг друга). Это будет в том случае, если разность хода в вакууме будет равна нечетному числу полуволн:
где \(m = 0, 1, 2, \ldots\) Равенство (17.3) есть условие интерференционного минимума.
Таким образом, интерференция света — наложение световых когерентных волн, в результате которого наблюдается устойчивая во времени картина чередования максимумов и минимумов интенсивности света.
Если когерентными источниками света являются две узкие параллельные щели (рис. 17.5), то на экране интерференционная картина представляет собой чередование светлых и темных полос, параллельных друг другу Как показывают расчеты (см. ниже "Примеры решения задач", задача 2), положение светлых полос относительно точки О определяется формулой
Расстояние между соседними максимумами
Как видно, \(\Delta x\) не зависит от порядка интерференционного максимума и является постоянной для данных \(\lambda\), D и l.
Главный максимум, соответствующий m = 0, находится в точке О Вверх и вниз от него, на равных расстояниях друг от друга расположены максимумы (минимумы) первого (m = 1), второго (m = 2) и т.д. порядков.
Эта картина справедлива лишь при освещении щелей монохроматическим светом. Если использовать белый свет, то интерференционные максимумы для различных длин волн согласно формуле (17.4) будут смещены друг относительно друга и будут иметь вид радужных полос. Только для m = 0 максимумы всех длин волн совпадают и в середине экрана будет наблюдаться белая полоса, по обе стороны от которой симметрично располагаются спектрально окрашенные полосы максимумов 1-го, 2-го и т.д. порядков.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 504-507.