Т. Закон Архимеда

Архимедова сила для жидкостей и газов

Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Для ее расчета рассмотрим тело кубической формы, находящееся в жидкости (рис. 1).

Рис. 1

На все грани тела, погруженного в жидкость, действуют силы давления.

Равнодействующая этих сил давления — выталкивающая сила:

\(~\vec F_A = \vec F_1 + \vec F_2 + \vec F_3 + \vec F_4 + \vec F_5 + \vec F_6.\)

Силы давления на боковые и на переднюю и заднюю грани уравновешиваются\[~\vec F_3 + \vec F_4 = 0, \vec F_5 + \vec F_6 = 0\].

На верхнюю грань действует сила

\(~F_1 = \rho gh_1 S.\)

На нижнюю грань — сила

\(~F_2 = \rho gh_2 S.\)

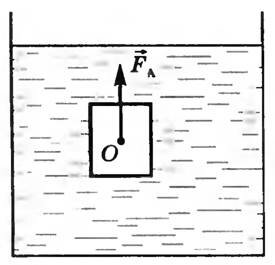
Равнодействующая этих сил направлена вертикально вверх, приложена к центру масс вытесненной телом жидкости — центру давления О (рис. 2) и представляет собой выталкивающую силу \(~\vec F_A\):

\(~F_A = F_2 - F_1 = \rho_0 g(h_2 - h_1) S = \rho_0 gh S = \rho_0 gV,\)

где V — объем погруженной в жидкость части тела, ρ₀ — плотность жидкости.

Рис. 2

\(~F_A = \rho_0 gV\) — закон Архимеда: на тело, погруженное в жидкость (газ), действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела, направленная вертикально вверх и приложенная в центре давления.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 102.