КС. ЭМИ

Магнитный поток

\(~\Phi = B \cdot S \cdot \cos \alpha\) ,

где Φ – магнитный поток (Вб); В – модуль вектора магнитной индукции (Тл); S – площадь контура (м²); α – угол между вектором магнитной индукции и нормалью (\(~\vec n\)) к контуру (рис. 1).

Рис. 1

ЭДС индукции

\(~E_i = -\frac {\Delta \Phi}{\Delta t},\)

где E_i – ЭДС индукции, возникающая в контуре при равномерном изменении магнитного потока (В); ΔΦ = Φ₂ - Φ₁ – изменение магнитного потока от Φ₁ до Φ₂ (Вб); Δt – время изменения магнитного потока (с); ΔΦ/Δt – скорость изменения магнитного потока (Вб/с или В).

• Эту формулу можно применять только при равномерном изменении магнитного потока.
• При увеличении магнитного потока (ΔΦ > 0), ЭДС отрицательная (ℰ_i < 0), т.е. индукционный ток имеет такое направление, что вектор магнитной индукции индукционного магнитного поля направлен против вектора магнитной индукции внешнего (изменяющегося) магнитного поля (рис. 2 а).
• При уменьшении магнитного потока (ΔΦ < 0), ЭДС положительная (E_i > 0), т.е. индукционный ток имеет такое направление, что вектор магнитной индукции индукционного магнитного поля направлен в одну и ту же сторону с вектором магнитной индукции внешнего (изменяющегося) магнитного поля (рис. 2 б).
• Знак «–» в формуле будем учитывать в задачах, где указано как изменяется (увеличивается или уменьшается) магнитный поток.

• 

  а
• 

  б

Рис. 2

Так как магнитный поток равен \(~\Phi = B \cdot S \cdot \cos \alpha\) , то он может изменяться:

• или только за счет изменения магнитной индукции поля, тогда

  \(~\Delta \Phi = (B_2 - B_1) \cdot S \cdot \cos \alpha\) ;

• или только за счет изменения площади контура, тогда

  \(~\Delta \Phi = B \cdot (S_2 - S_1) \cdot \cos \alpha\) ;

• или только за счет поворота контура в магнитном поле, тогда

  \(~\Delta \Phi = B \cdot S \cdot (\cos \alpha_2 - \cos \alpha_1)\) ;

• или одновременно за счет изменения нескольких параметров, тогда

  \(~\Delta \Phi = B_2 \cdot S_2 \cdot \cos \alpha_2 - B_1 \cdot S_1 \cdot \cos \alpha_1\) .

При любом способе изменения магнитного потока в контуре возникает ЭДС индукции.

Индукционный ток

\(~I_i = -\frac {E_i}{R},\)

где I_i – индукционный ток в контуре (А), E_i – ЭДС индукции (В), R – сопротивление контура (Ом).

План определения направления индукционного тока:

1. Установите направление вектора магнитной индукции внешнего поля (\(~\vec B\)).
2. Выясните, как изменяется (увеличивается или уменьшается) поток магнитной индукции этого поля через поверхность контура.
3. Используя правило Ленца, установите направление вектора магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) :
   • если поток магнитной индукции через контур увеличивается, то вектор магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) направлен в противоположную сторону вектора магнитной индукции внешнего поля (\(~\vec B\)) ;
   • если поток магнитной индукции через контур уменьшается, то вектор магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) направлен в ту же сторону, что и вектор магнитной индукции внешнего поля (\(~\vec B\)) .
4. Используя правило правой руки, по направлению вектора магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) найдите направление индукционного тока.

ЭДС индукции движущегося проводника

Индукционный ток в проводниках, движущихся в магнитном поле, возникает за счет действия на свободные заряды проводника силы Лоренца. Поэтому направление индукционного тока в проводнике будет совпадать с направлением составляющей силы Лоренца на этот проводник.

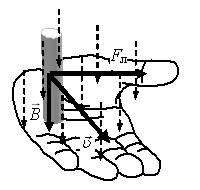
С учетом этого можно сформулировать следующее правило левой руки для определения направления индукционного тока в движущемся проводнике: нужно расположить левую руку так, чтобы вектор магнитной индукции входил в ладонь, четыре пальца совпадали с направлением движения проводника, тогда отставленный на 90° большой палец укажет направление индукционного тока (рис. 3).

Рис. 3

• Если проводник движется вдоль вектора магнитной индукции, то индукционного тока не будет (сила Лоренца равна нулю).
• Ток не может идти поперек проводника (заряды под действием силы Лоренца смещаются к стенкам проводника и создавать ток не будут) (рис. 4).

Рис. 4

\(~E_i = B \cdot \upsilon \cdot l \cdot \cos \alpha ,\)

где E_i – ЭДС индукции движущегося проводника (В); υ – скорость движения проводника (м/с); В – модуль вектора магнитной индукции (Тл); l – длина проводника (м); α – угол между направлением движения проводника и вектором магнитной индукции.

Самоиндукция

\(E_{si} = -L \cdot \frac{\Delta I}{\Delta t},\)

где E_si – ЭДС самоиндукции (В); L – индуктивность катушки (Гн); ΔI = I₂ - I₁ – изменение силы тока от I₁ до I₂ (А); Δt – время изменения силы тока (с); ΔI/Δt – скорость изменения силы тока (А/с).

• Эту формулу можно применять только при равномерном изменении силы тока.
• При увеличении тока (ΔI > 0), ЭДС отрицательная (E_si < 0), т.е. индукционный ток направлен в противоположную сторону тока источника.
• При уменьшении тока (ΔI < 0), ЭДС положительная (E_si > 0), т.е. индукционный ток направлен в ту же сторону, что и ток источника.
• Знак «–» учитывать будем в задачах, где указано как изменяется (увеличивается или уменьшается) сила тока.

Во всех задачах данной темы считаем, что сила тока изменяется равномерно.

Индуктивность контура

\(~L = \frac{\Phi}{I}\) ,

где L – индуктивность контура (катушки) (Гн); Φ – магнитный поток (Вб); I – сила тока (А).

• Магнитный поток внутри катушки, состоящей из N витков, равен сумме магнитных потоков, создаваемых каждым витком, т.е. Φ = N·Φ₁ .

\(~L = \mu_0 \cdot N^2 \cdot \frac{S}{l}\) ,

где L – индуктивность катушки (соленоида) (Гн); μ₀ – магнитная постоянная, равная 4π·10^-7 Тл·м/А ; l – длина катушки (м); N – число витков; S – площадь поперечного сечения катушки (м²).

Энергия магнитного поля

\(~W_m = \frac{L \cdot I^2}{2}\) ,

где W_m – энергия магнитного поля тока (катушки) (Дж); L – индуктивность контура (катушки) (Гн); I – сила тока в катушке (А).

Используя формулы\[~W_m = \frac{L \cdot I^2}{2}\] и \(~\Phi = L \cdot I\) , где W_m – энергия магнитного поля тока (катушки) (Дж); L – индуктивность контура (катушки) (Гн); I – сила тока в катушке (А), Ф – магнитный поток (Вб) – зная из них любые две величины, можно найти две остальные.