КС. Статика
Статика
Условие равновесия тела, не имеющего оси вращения:
где \(~\vec F_1 , \vec F_2 , \ldots\) – силы, действующие на тело (Н).
Плечо l – это наименьшее расстояние между точкой (осью) вращения и линией действия силы.
где М – момент силы (Н·м); F – модуль силы (Н); l – плечо силы (м).
Условимся:
- если момент силы вращает (пытается вращать) тело по часовой стрелке, будем считать такой момент силы положительным;
- если вращает против часовой стрелки – отрицательным.
Условие равновесия тела, имеющего закрепленную ось вращения:
где М1, М2, … – моменты сил, приложенных к телу (Н·м).
При решении задач на равновесие тела, имеющего ось вращения, будем использовать следующий план:
- Сделайте чертеж, укажите силы, действующие на тело, и ось (точку) вращения.
- Определите плечи сил, моменты сил и их знаки.
- Запишите условие равновесия тела, имеющего закрепленную ось вращения: М1 + М2 + … = 0.
- Решите полученные уравнения.
- На рычаг действует сила реакции опоры N, момент силы которой относительно опоры равен 0, т.к. плечо этой силы равно 0. Поэтому в задачах первого уровня эту силы не учитываем.
- Центр тяжести у однородного тела совпадает с геометрическим центром.
- Центр тяжести может находится и вне тела.
| Виды равновесия | Признаки |
|---|---|
| Устойчивое | при любых малых отклонениях от положения равновесия (точка О) тело будет стремиться возвратиться в начальное положение (рис. 1 а). |
| Неустойчивое | при любых малых отклонениях от положения равновесия (точка О) тело будет стремиться еще больше отклониться от начального положения (рис. 1 б). |
| Безразличное | при любых малых отклонениях от положения равновесия (точка О) тело не будет стремиться возвратиться в начальное положение или еще больше отклониться от начального положения (рис. 1 в). |
Пусть на тело действует параллельные силы \(~\vec F_1\) и \(~\vec F_2\) , точки приложения которых А и В соответственно. Тогда равнодействующая \(~\vec R = \vec F_1 + \vec F_2\) будет направлена вдоль параллельной этим силам прямой а (линии действия равнодействующей), а точка приложения О равнодействующей \(~\vec R\) будет лежать на пересечении прямой АВ и а (рис. 2). Кроме того, тело будет находиться в равновесии относительно точки О.
С учетом этого при нахождении равнодействующей \(~\vec R\) параллельных сил \(~\vec F_1\) и \(~\vec F_2\) , действующих на тело, воспользуемся следующим способом:
- проведите прямую, проходящую через точки А и В приложения сил \(~\vec F_1\) и \(~\vec F_2\) ;
- используя условие равновесия тела М1 + М2 + … = 0, найдите местоположение точки О на прямой АВ, относительно которой тело будет находиться в равновесии. Точка О – точка приложения равнодействующей силы;
- равнодействующая:
- R = F1 + F2 и направлена в ту же сторону, что и силы \(~\vec F_1\) и \(~\vec F_2\) , если силы направлены в одну сторону;
- R = |F1 - F2| и направлена в сторону большей силы, если силы направлены в противоположные стороны.
При равновесии твердого тела сумма моментов всех внешних сил, действующих на него относительно любой оси, равна нулю. Поэтому в задачах можно выбирать ось вращения таким образом, чтобы уменьшить в уравнении число неизвестных величин.
Сила тяжести системы тел – это равнодействующая сил тяжести частей этой системы. Тогда поиск центра тяжести системы сводится к нахождению точки приложения равнодействующей параллельных сил, направленных в одну сторону.
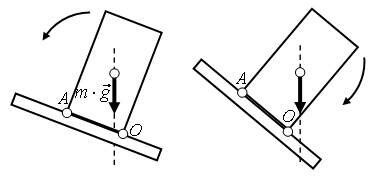
Для равновесия тела, стоящего на плоскости, необходимо, чтобы вертикаль, проходящая через центр тяжести тела, пересекала поверхность, ограниченную опорой (АО), т.к. в этом случае момент силы тяжести стремится повернуть тело вокруг точки О против часовой стрелки (рис. 3 а), и тело находится в устойчивом равновесии. В противном случае (т.е. вертикаль, проходящая через центр тяжести тела, не пересекает поверхность, ограниченную опорой (АО)) момент силы тяжести стремится повернуть тело вокруг точки О по часовой стрелке (рис. 3 б), и тело опрокидывается.
Устойчивость тела улучшается, если увеличивается площадь опоры.
Устойчиво то положение тела, в котором его потенциальная энергия имеет минимальное значение, а, следовательно, ниже центр тяжести тела.