КС. Магнитное поле
Вектор магнитной индукции
Направление вектора
За направление вектора магнитной индукции принято следующие направления:
- для магнитной стрелки (свободно вращающейся в магнитном поле) – от южного (S) полюса стрелки к северному (N) (рис. 1 а);
- для плоского магнита: вдоль магнита – от южного (S) полюса магнита к северному (N) (рис. 1 б), по бокам магнита – от северного (N) полюса магнита к южному (S) (рис. 1 в – пунктиром показаны линии индукции);
- между полюсами магнитов (подковообразного магнита) – от северного (N) полюса магнита к южному (S) (рис. 1 г).
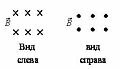
В данной теме для изображения векторов, перпендикулярных плоскости рисунка применяют условные обозначения: крестики и точки.
Например:
а) по проводнику течет ток (рис. 2 а);
б) в данной области существует однородное магнитное поле с индукцией \(~\vec B\) (рис. 2 б).
Тогда в плоскости γ направление векторов будем изображать так, как на рисунках 3 а (окружности на данном рисунке – это сечения проводника) и 3 б.
Для ориентации в трехмерном пространстве будем использовать следующие названия направлений (рис. 4 а и б): OC – «вправо»; OB – «вниз»; OD – «влево»; OA – «вверх»; OE – «к нам»; OF – «от нас». Плоскость γ лежит в плоскости листа.
Для определения направления вектора магнитной индукции проводника с током применяют правило буравчика или правило правой руки:
а) для прямого проводника с током правило правой руки имеет следующий вид: большой палец правой руки, отставленный на 90°, направляем по току, тогда четыре согнутых пальца, обхватывающие проводник, укажут направление вектора магнитной индукции (рис. 5 а).
б) для витка (катушки) с током правило правой руки имеет следующий вид: четыре согнутых пальца правой руки, обхватывающей виток (катушку), направляем по току, тогда большой палец, отставленный на 90°, укажет направление вектора магнитной индукции в центре витка (рис. 5 б).
Значения вектора
где Bpr – индукция магнитного поля бесконечного прямолинейного проводника с током на расстоянии l (Тл); μ0 – магнитная постоянная, равная 4π·10-7 Тл·м/А ; I – сила тока в проводнике (А); l – расстояние от проводника до данной точки (м).
В данной теме считаем, что проводник расположен в вакууме.
где Bkr – индукция магнитного поля в центре кругового тока (кольца) (Тл); μ0 – магнитная постоянная, равная 4π·10-7 Тл·м/А ; I – сила тока (А); r – радиус кольца с током (м).
где Bc – индукция магнитного поля внутри (середине) цилиндрической катушки (соленоида) (Тл); μ0 – магнитная постоянная, равная 4π·10-7 Тл·м/А ; N – число витков катушки; I – сила тока (А); l – длина катушки (м).
Магнитные свойства вещества
где μ – магнитная проницаемость, табличная величина; B – магнитная индукция в веществе (Тл); B0 – магнитная индукция внешнего (намагничивающего) поля (Тл).
Тогда с учетом магнитной проницаемости среды
- индукция магнитного поля бесконечного прямолинейного проводника с током на расстоянии l
-
\(~B_{pr} = \frac{\mu \cdot \mu_0 \cdot I}{2 \pi \cdot l}\) ;
-
- индукция магнитного поля в центре кругового тока (кольца)
-
\(~B_{kr} = \frac{\mu \cdot \mu_0 \cdot I}{2 r}\) ;
-
- индукция магнитного поля внутри (середине) цилиндрической катушки (соленоида)
-
\(~B_c = \frac{\mu \cdot \mu_0 \cdot I \cdot N}{l}\) .
-
Сила Ампера
Для определения направления силы Ампера применяют правило левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная составляющая к проводнику вектора индукции (\(~\vec B\)) входила в ладонь, а четыре вытянутых пальца указывали бы направление тока (I), то отогнутый на 90° большой палец укажет направление силы Ампера (\(~\vec F_A\)) (рис. 6).
где FA – сила Ампера (Н); В – модуль вектора магнитной индукции (Тл); I – сила тока (А); l – длина проводника (м); α – угол между проводником (направлением тока в проводнике) и направлением вектора магнитной индукции.
Вращающий момент сил
где В – модуль вектора магнитной индукции (Тл); Mmax – максимальный вращающий момент сил, действующий на рамку с током, находящуюся в магнитном поле (Н·м); I – сила тока в рамке (А); S – площадь рамки (м2).
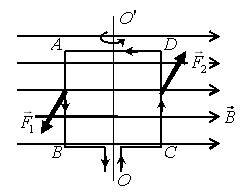
Поместим в однородном магнитном поле с индукцией (\(~\vec B\)) прямоугольную рамку с током ABCD (рис. 7 а – вид сбоку; рис. 7 б – вид сверху), где AB = a, AD = b, β – угол между перпендикуляром к рамке и вектором магнитной индукции.
На участки AD и BC магнитное поле действуют с силами, которые меняются от нуля до максимального значения (в зависимости от угла поворота рамки β) и стремятся растянуть рамку (на рис. 8 а эти силы не указаны). На участки AB и CD магнитное поле действуют с постоянными силами \(~\vec F_1\) и \(~\vec F_2\) , которые направлены в противоположные стороны (на рис. 7 а силы направлены перпендикулярно плоскости рисунка) и стремятся повернуть рамку вокруг оси OO´. Таким образом, эти силы \(~\vec F_1\) и \(~\vec F_2\) создают вращающий момент M = F1·l1 + F2·l2, где F1 = F2 = I·B·l (угол α = 90°), l1 = l2 = AD/2 ·sin β = b/2 ·sin β, l = AB = CD = a. Тогда
где S = a·b – площадь рамки.
Момент сил будет максимальным при β = 90° (рамка расположена вдоль линий индукции)
Примечание. Эта формула верна для плоской рамки произвольной формы.
Сила Лоренца
Для определения направления силы Лоренца применяют правило левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая к скорости частицы (\(~\vec \upsilon\)) магнитной индукции (\(~\vec B\)) входила в ладонь, а четыре вытянутых пальца указывали бы направления движения положительно заряженной частицы, то отогнутый на 90° большой палец укажет направление силы Лоренца (\(~\vec F_L\)) , действующей со стороны магнитного поля на частицу (рис. 8 а). Для отрицательной частицы четыре вытянутых пальца направляют против движения частицы (рис. 8 б).
где FL – сила Лоренца (Н); q – модуль заряда движущейся частицы (Кл); υ – скорость частицы (м/с); В – модуль вектора магнитной индукции (Тл); α – угол между скоростью движения положительного заряда и вектором магнитной индукции.
Движение заряженной частицы в магнитном поле
- Если скорость υ заряженной частицы массой m направлена вдоль вектора магнитной индукции поля, то частица будет двигаться по прямой с постоянной скоростью (сила Лоренца FL = 0, т.к. α = 0°) (рис. 9 а).
- Если скорость υ заряженной частицы массой m перпендикулярна вектору магнитной индукции поля, то частица будет двигаться по окружности радиуса R, плоскость которой перпендикулярна линиям магнитной индукции (рис. 9 б). Тогда 2-ой закон Ньютона можно записать в следующем виде:
-
\(~m \cdot a_c = F_L\) , - где \(~a_c = \frac{\upsilon^2}{R}\) , \(~F_L = q \cdot B \cdot \upsilon \cdot \sin \alpha\) , α = 90°, т.к. скорость частицы перпендикулярна вектору магнитной индукции.
- Тогда \(~\frac{m \cdot \upsilon^2}{R} = q \cdot B \cdot \upsilon\) .
-
- 3. Если скорость υ заряженной частицы массой m направлена под углом α (0 < α < 90°) к вектору магнитной индукции поля, то частица будет двигаться по спирали радиуса R и шагом h (рис. 10 а, в).
Для описания движения частицы можно использовать следующий способ: разложить скорость υ заряженной частицы на две составляющие υ⊥ = υ·sin α – перпендикулярную (к линии индукции) и υ|| = υ·cos α – параллельную (к линии индукции) (рис. 10 б). Перпендикулярная составляющая скорости υ⊥ вызывает движение частицы по окружности радиуса R, плоскость которой перпендикулярна линиям магнитной индукции, а параллельная υ|| – равномерное движение вдоль линии индукции (рис. 10 в).
Для описания движения по окружности, перпендикулярно линиям магнитной индукции, используем уравнение \(~\frac{m \cdot \upsilon_{\perp}^2}{R} = q \cdot B \cdot \upsilon_{\perp}\) или \(~\frac{m \cdot \upsilon_{\perp}}{R} = q \cdot B\) , т.к. \(~m \cdot a_c = F_L\) , где \(~F_L = q \cdot B \cdot \upsilon_{\perp}\) , \(~a_c = \frac{\upsilon_{\perp}^2}{R}\) .
Для описания движения вдоль линий магнитной индукции, используем уравнение h = υ||·T , где h – это шаг винтовой линии (спирали), Т – время, за которое частица совершит полный оборот (период).