КС. Интерференция света

Оптическая разность хода

\(~\Delta = n_1 \cdot r_1 - n_2 \cdot r_2\) ,

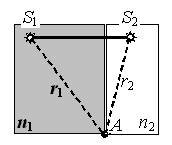
где Δ – оптическая разность хода двух лучей в точке А (м); n₁ и n₂ – абсолютные показатели преломления двух сред соответственно, табличные величины; r₁ и r₂ – расстояния от источников лучей S₁ и S₂ до точки А (м) (рис. 1).

Рис. 1

Разность |r₁ - r₂| называют геометрической разностью хода.

\(~\varphi_1 - \varphi_2 = \frac{2 \pi \cdot \Delta}{\lambda} \) ,

где φ₁ - φ₂ – разность фаз колебаний (рад); Δ – оптическая разность хода двух лучей (м); λ – длина волны (м).

Интерференция

Условие максимума освещенности при интерференции:

\(~\Delta = k \cdot \frac{\lambda}{2}\) , где k = 2m – четное число;

условие минимума освещенности при интерференции:

\(~\Delta = k \cdot \frac{\lambda}{2}\) , где k = 2m + 1 – нечетное число ,

Δ – оптическая разность хода двух лучей (м); λ – длина волны (м); m – некоторое целое число (m = 0, ±1, ±2, …).

Условие максимума освещенности при интерференции:

\(~\varphi_1 - \varphi_2 = k \cdot \pi\) , где k = 2m – четное число;

условие минимума освещенности при интерференции:

\(~\varphi_1 - \varphi_2 = k \cdot \pi\) , где k = 2m + 1 – нечетное число ,

φ₁ - φ₂ – разность фаз колебаний (рад); m – некоторое целое число (m = 0, ±1, ±2, …).

Рекомендация по решению задач

• Если необходимо найти разность приближенно равных чисел (например, а и b), можно применить следующий математический прием:

1. найти а² - b²;
2. расписать а² - b² = (а - b) · (а + b) ;
3. так как а ≈ b , то а + b ≈ 2а.

   Тогда \(~a - b = \frac{a^2 - b^2}{2a}\) .

• При переходе в другую среду период (частота) волны не меняется.
• При отражении луча от среды с меньшим показателем преломления фаза колебаний волны не меняется. При отражении луча от среды с большим показателем преломления, волна меняет фазу колебаний на противоположную (на π), что равносильно потере полуволны (λ/2).