КС. Дифракция света

Дифракция света

Условие максимума освещенности при дифракции:

\(~\Delta = m \cdot \lambda\) ,

где Δ – оптическая разность хода (м); m – порядок дифракционного максимума (порядок спектра) (m = 0, ±1, ±2, …) ; λ – длина волны (м).

Дифракция света на одной щели

Условие минимума освещенности при дифракции на одной щели:

\(~b \cdot \sin \beta = k \cdot \frac{\lambda}{2}\) , где k = 2m – четное число, m = ±1, ±2, …;

условие максимума освещенности при дифракции на одной щели:

\(~b \cdot \sin \beta = k \cdot \frac{\lambda}{2}\) , где k = 0 и k = 2m + 1 – нечетное, m = 0, ±1, ±2, … ,

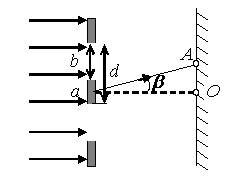
b – ширина щели (м); β – угол отклонения лучей от перпендикуляра к плоскости щели или угол направления на m-ую интерференционную полосу (рад или град) (рис. 1); λ – длина волны (м); m – порядковый номер максимума или минимума.

Рис. 1

• Для того, чтобы наблюдать дифракцию на одной щели, необходимо за решеткой поместить линзу, в фокальной плоскости которой и будет находиться экран. Тогда все параллельные лучи будут пересекаться в точках экрана (рис. 2). Но если поместить линзу вблизи щели, то точки А и А₁ совпадут. А так как линза не изменяет оптической разности хода лучей, то при решении задач ее можно не учитывать.

Рис. 2

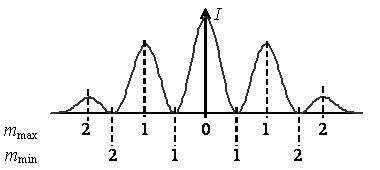
Отсчет порядкового номера максимума или минимума освещенности при дифракции на одной щели идет от центра (самой яркой точки) интерференционной картины (рис. 3).

Рис. 3

Дифракционная решетка

\(~d = \frac{l}{N}\) ,

где d – постоянная или период дифракционной решетки (м); l – длина решетки, на которую приходится N штрихов (м); N – число штрихов решетки, приходящихся на некоторую длину l решетки.

\(~d \cdot \sin \beta = m \cdot \lambda\) ,

где d – постоянная или период дифракционной решетки (м); β – угол отклонения лучей от нормали к плоскости щели (рад или град) (рис. 4); λ – длина волны (м); m – порядковый номер дифракционного максимума или спектра (m = 0, ±1, ±2, …).

Рис. 4

• Для того, чтобы наблюдать интерференционную картину от дифракционной решетки, необходимо за решеткой поместить линзу, в фокальной плоскости которой и будет находиться экран. Тогда все параллельные лучи будут пересекаться в точках экрана (рис. 5). Но если поместить линзу вблизи дифракционной решетки, то точки А и А₁ совпадут. А так как линза не изменяет оптической разности хода лучей, то при решении задач ее можно не учитывать.

Рис. 5